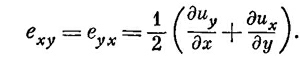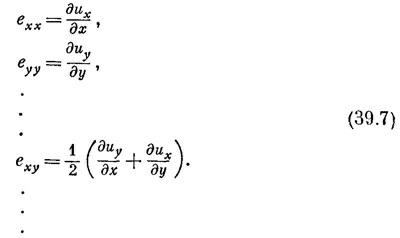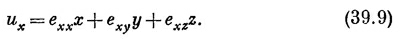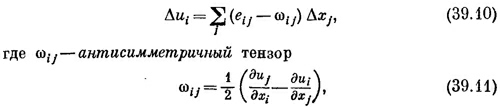| Обучение и материалы |
|---|
| Физический справочник |
| Формулы по физике |
| Шпаргалки по физике |
| Энциклопедия |
| Репетиторы по физике |
| Работа для физиков |
| Быстрый устный счет |
| Виртуальные лабораторные |
| Опыты по физике |
| ЕГЭ онлайн |
| Онлайн тестирование |
| Ученые физики |
| Необъяснимые явления |
| Ваша реклама на сайте |
| Разное |
| Контакты |
| Спецкурс |
|---|
| Фейнмановские лекции |
|
В мире больших скоростей |
Введение в теорию относительности |
|
Лекции по биофизике |
| Лекции по ядерной физике |
| Ускорение времени... |
| Лазеры |
| Нанотехнологии |
| Книги |
| полезное |
|---|
| Смешные анекдоты о физике
Готовые шпоры по физике Физика в жизни Ученые и деньги Нобелевские лауреаты Фото Видео Карта сайта |
| На заметку |
|---|
| Если вам понравился сайт, предлагаем разместить нашу кнопку |
| Дополнительно |
|---|
|
Компьютерные программы по физике 
Физика и юмор 
Онлайн тестирование по физике 
|
Тензор деформации
Мы будем записывать uх следующим образом:
Разумеется, константа пропорциональности ехх— это то же, что наше старое отношение Δl/l. (Скоро вы увидите, почему нам потребовался двойной индекс.)
Это число, которое теперь будет функцией х, у и z, описывает величину растяжения в направлении оси х по всему куску желе. Возможны, конечно, растяжения и в направлении осей у и z. Мы будем описывать их величинами
а перемещение в направлении у пропорционально х:
Таким образом, деформацию сдвигового типа можно описать с помощью
Теперь вы сочтете, что при неоднородной деформации обобщенную деформацию сдвига можно описать, определив величины exy, eyx следующим образом:
Однако здесь есть некая трудность. Предположим, что перемещения их и иу имеют вид
Для чистого вращения оба они равны нулю, но для чистого сдвига мы получаем, как и хотели, еху = еyx .
Они образуют компоненты тензора деформации. Поскольку тензор этот симметричен (согласно нашему определению, еxy всегда равно еyx ), то на самом деле различных чисел здесь только шесть. Вы помните (см. гл. 31) общее свойство всех тензоров — элементы его преобразуются при повороте подобно произведению компонент двух векторов. (Если А и В — векторы, то C¡j = AiBj— тензор.) А каждое наше е¡j есть произведение (или сумма таких произведений) компонент вектора u= (ux, uy, uz) и оператора V = (∂/∂x, ∂/∂y, ∂/∂z), который, как
где индексы i и j могут принимать значения 1, 2 или 3.
(Начало координат выбрано в точке, где u равно нулю.) В этих случаях тензор деформации eij дает соотношение между двумя векторами — вектором координаты r = (х, у, z) и вектором перемещения u = (их, иy , иz).
описывающий поворот. Нам незачем беспокоиться о поворотах; займемся только деформацией, которая описывается симметричным тензором e¡j. СМОТРИТЕ ТАКЖЕ:Социальные комментарии Cackle |
При использовании материалов сайта ссылка на www.all-fizika.com обязательна.

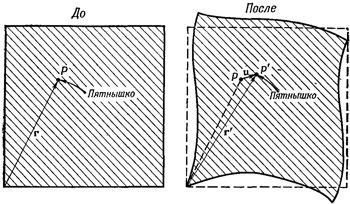 В предыдущей главе мы говорили о возмущениях упругих тел в простых случаях. В этой главе мы посмотрим, что может происходить внутри упругого материала в общем случае. Как описать условия напряжения и деформации в большом куске желе, скрученном и сжатом каким-то очень сложным образом? Для этого необходимо описать локальную деформацию в каждой точке упругого тела, а это можно сделать, задав в ней набор шести чисел — компонент симметричного тензора. Ранее (в гл. 31) мы говорили о тензоре напряжений, теперь же нам потребуется тензор деформации.
В предыдущей главе мы говорили о возмущениях упругих тел в простых случаях. В этой главе мы посмотрим, что может происходить внутри упругого материала в общем случае. Как описать условия напряжения и деформации в большом куске желе, скрученном и сжатом каким-то очень сложным образом? Для этого необходимо описать локальную деформацию в каждой точке упругого тела, а это можно сделать, задав в ней набор шести чисел — компонент симметричного тензора. Ранее (в гл. 31) мы говорили о тензоре напряжений, теперь же нам потребуется тензор деформации.
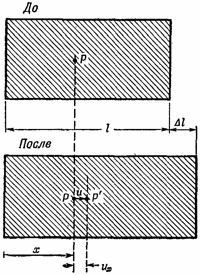 Перемещение u зависит, конечно, от точки Р, из которой оно выходит так, что и есть векторная функция от r или от (х, у, z).
Перемещение u зависит, конечно, от точки Р, из которой оно выходит так, что и есть векторная функция от r или от (х, у, z).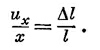
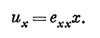

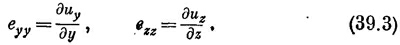
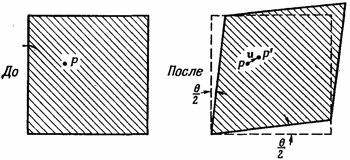 Кроме того, нам нужно описать деформации типа сдвигов. Вообразите, что в первоначально невозмущенном желе вы выделили маленький кубик. Нажав на желе, мы изменяем его форму, и наш кубик может превратиться в параллелограмм (фиг. 39.3). При такой деформации перемещение в направлении х каждой частицы пропорционально ее координате у:
Кроме того, нам нужно описать деформации типа сдвигов. Вообразите, что в первоначально невозмущенном желе вы выделили маленький кубик. Нажав на желе, мы изменяем его форму, и наш кубик может превратиться в параллелограмм (фиг. 39.3). При такой деформации перемещение в направлении х каждой частицы пропорционально ее координате у:

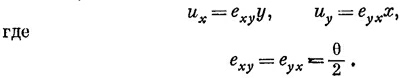
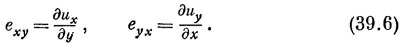
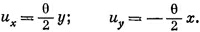
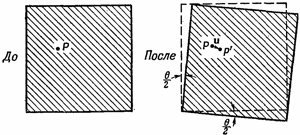 Они напоминают уравнения (39.4) и (39.5), за исключением того, что при uy, стоит обратный знак. При таком перемещении маленький кубик из желе претерпевает простой поворот на угол θ/2 (фиг. 39.4). Никакой деформации здесь вообще нет, а есть просто вращение в пространстве. При этом никакого возмущения материала не происходит, а относительное положение всех атомов совершенно не изменяется. Нужно как-то устроить так, чтобы чистое вращение не входило в наше определение деформации сдвига. Указанием может послужить то, что если диy /дх и дих/ду равны и противоположны, никакого напряжения нет; этого можно добиться, определив
Они напоминают уравнения (39.4) и (39.5), за исключением того, что при uy, стоит обратный знак. При таком перемещении маленький кубик из желе претерпевает простой поворот на угол θ/2 (фиг. 39.4). Никакой деформации здесь вообще нет, а есть просто вращение в пространстве. При этом никакого возмущения материала не происходит, а относительное положение всех атомов совершенно не изменяется. Нужно как-то устроить так, чтобы чистое вращение не входило в наше определение деформации сдвига. Указанием может послужить то, что если диy /дх и дих/ду равны и противоположны, никакого напряжения нет; этого можно добиться, определив