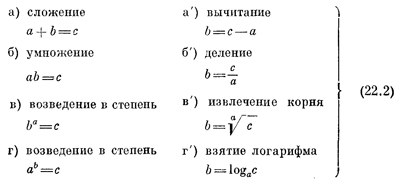| Обучение и материалы |
|---|
| Физический справочник |
| Формулы по физике |
| Шпаргалки по физике |
| Энциклопедия |
| Репетиторы по физике |
| Работа для физиков |
| Быстрый устный счет |
| Виртуальные лабораторные |
| Опыты по физике |
| ЕГЭ онлайн |
| Онлайн тестирование |
| Ученые физики |
| Необъяснимые явления |
| Ваша реклама на сайте |
| Разное |
| Контакты |
| Спецкурс |
|---|
| Фейнмановские лекции |
|
В мире больших скоростей |
Введение в теорию относительности |
|
Лекции по биофизике |
| Лекции по ядерной физике |
| Ускорение времени... |
| Лазеры |
| Нанотехнологии |
| Книги |
| полезное |
|---|
| Смешные анекдоты о физике
Готовые шпоры по физике Физика в жизни Ученые и деньги Нобелевские лауреаты Фото Видео Карта сайта |
| На заметку |
|---|
| Если вам понравился сайт, предлагаем разместить нашу кнопку |
| Дополнительно |
|---|
|
Компьютерные программы по физике 
Физика и юмор 
Онлайн тестирование по физике 
|
Обратные операции
Кроме прямых операций сложения, умножения и возведения в степень, существуют обратные операции. Их можно определить так. Предположим, что нам заданы а и с; как найти b, удовлетворяющее уравнениям а+Ь=с, ab=c, ba=c? Если a+b=c, то b определяется при помощи вычитания: b=с—а. Столь же проста операция деления: если аb=с, то Ь=с/а; это решение уравнения aЬ=с «задом наперед». Если вам встретится степень: bа=с, то надо запомнить, что b называется корнем а-й степени из с. Например, на вопрос: «Какое число, будучи возведенным в куб, дает 8?» — следует отвечать: «Кубический корень из 8, т. е. 2». Обратите внимание, что, когда дело доходит до степени, появляются две обратные операции. Действительно, ведь раз аb и Ьа— различные числа, то можно задать и такой вопрос: «В какую степень надо возвести 2, чтобы получить 8?» В этом случае приходится брать логарифм. Если аb=с, то b=-logac. He надо пугаться громоздкой записи числа b в этом случае; находить его так же просто, как и результаты других обратных операций. Хотя логарифм «проходят» гораздо позже корня, это такая же простая вещь: просто-напросто это разного сорта решения алгебраических уравнений. Выпишем вместе прямые и обратные операции:
В чем же идея? Выписанные соотношения верны для целых чисел, потому что они выводятся из определений сложения, умножения и возведения в степень. Подумаем, нельзя ли расширить класс объектов, которые по-прежнему будут обозначаться буквами а, b и с и для которых по-прежнему будут верны все сформулированные нами правила, хотя сложение уже нельзя будет понимать как последовательное увеличение числа на единицу, а возведение в степень — как последовательное перемножение целых чисел. СМОТРИТЕ ТАКЖЕ:Социальные комментарии Cackle |
© All-Физика, 2009-2026
При использовании материалов сайта ссылка на www.all-fizika.com обязательна.
При использовании материалов сайта ссылка на www.all-fizika.com обязательна.