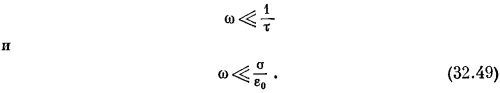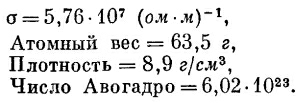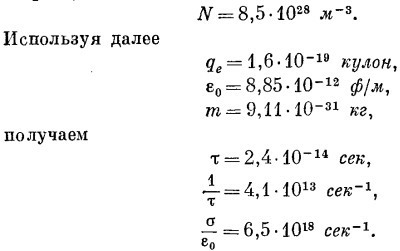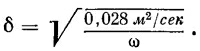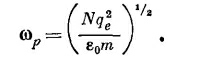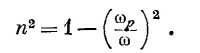| Обучение и материалы |
|---|
| Физический справочник |
| Формулы по физике |
| Шпаргалки по физике |
| Энциклопедия |
| Репетиторы по физике |
| Работа для физиков |
| Быстрый устный счет |
| Виртуальные лабораторные |
| Опыты по физике |
| ЕГЭ онлайн |
| Онлайн тестирование |
| Ученые физики |
| Необъяснимые явления |
| Ваша реклама на сайте |
| Разное |
| Контакты |
| Спецкурс |
|---|
| Фейнмановские лекции |
|
В мире больших скоростей |
Введение в теорию относительности |
|
Лекции по биофизике |
| Лекции по ядерной физике |
| Ускорение времени... |
| Лазеры |
| Нанотехнологии |
| Книги |
| полезное |
|---|
| Смешные анекдоты о физике
Готовые шпоры по физике Физика в жизни Ученые и деньги Нобелевские лауреаты Фото Видео Карта сайта |
| На заметку |
|---|
| Если вам понравился сайт, предлагаем разместить нашу кнопку |
| Дополнительно |
|---|
|
Компьютерные программы по физике 
Физика и юмор 
Онлайн тестирование по физике 
|
Низкочастотное и высокочастотное приближения. Глубина скин-слоя и плазменная частота
Наш результат для показателя преломления в металлах — формула (32.42) — предсказывает для распространения волн с разными частотами совершенно различные характеристики. Прежде всего давайте посмотрим, что получается при низких частотах. Если величина ω достаточно мала, то (32.42) можно приближенно записать в виде
Возведением в квадрат можно проверить, что
Вещественная и мнимая части n имеют одну и ту же величину. С такой большой мнимой частью n волны в металлах затухают очень быстро. В соответствии с выражением (32.36) амплитуда волны, идущей в направлении оси z, уменьшается как
Но что все-таки мы понимаем под «низкими» частотами? Взглянув на уравнение (32.42), мы видим, что его можно приближенно заменить уравнением (32.44), только когда ωτ много меньше единицы и когда (ωε0/σ также много меньше единицы, т. е. наше низкочастотное приближение применимо при
Давайте посмотрим, какие частоты соответствуют этому приближению для такого типичного металла, как медь. Для вычисления т воспользуемся уравнением (32.43), а для вычисления σ/ε0 — известными значениями σ и ε0. Справочник дает нам такие данные:
Если мы предположим, что на каждый атом приходится по одному свободному электрону, то число электронов в кубическом метре будет равно
Таким образом, для частот, меньших чем приблизительно 1012 гц, медь будет иметь описанное нами «низкочастотное» поведение. (Это будут волны с длиной, большей 0,3 мм, т. е. очень короткие радиоволны!)
Для микроволн с частотой 10 000 Мгц (3-сантиметровые волны)
т. е. волны проникают на очень малое расстояние.
Для высокочастотных волн показатель преломления в металлах становится чисто вещественным и меньшим единицы! Это следует также из выражения (32.38), если пренебречь диссипативным членом с γ, что может быть сделано при очень больших значениях ω. Выражение (32.38) дает при этом
что, разумеется, эквивалентно уравнению (32.50). Раньше нам уже встречалась величина (Nqe2/ε0m)1/2, которую мы назвали плазменной частотой (см. гл. 7, § 3, вып. 5):
Таким образом, (32.50) или (32.51) можно переписать в виде
Эта плазменная частота является своего рода «критической».
Вас может удивить, почему плазменная частота ωр должна иметь отношение к распространению волн в металлах. Плазменная частота появилась у нас в гл. 7 (вып. 5) как собственная частота колебаний плотности свободных электронов. (Электрическое расталкивание группы электронов и их инерция приводят к колебаниям плотности.) Продольные волны плазмы резонируют при частоте ωр. Но сейчас мы говорим о поперечных волнах, и мы уже нашли, что при частотах, меньших ωр, происходит их поглощение. (Это очень интересное и отнюдь не случайное совпадение.) СМОТРИТЕ ТАКЖЕ:Социальные комментарии Cackle |
При использовании материалов сайта ссылка на www.all-fizika.com обязательна.


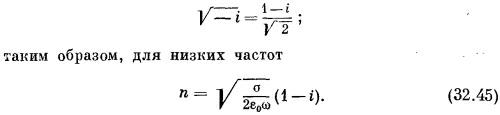
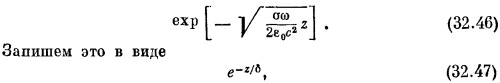
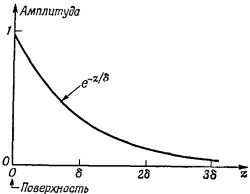 где δ — это то расстояние, на котором амплитуда волны уменьшается в е=2,72 раза, т. е. приблизительно в 3 раза. Амплитуда такой волны, как функция от z, показана на фиг. 32.3. Поскольку электромагнитные волны проникают в глубь металла только на это расстояние, величина δ называется глубиной скин-слоя и определяется выражением
где δ — это то расстояние, на котором амплитуда волны уменьшается в е=2,72 раза, т. е. приблизительно в 3 раза. Амплитуда такой волны, как функция от z, показана на фиг. 32.3. Поскольку электромагнитные волны проникают в глубь металла только на это расстояние, величина δ называется глубиной скин-слоя и определяется выражением