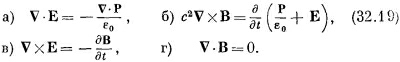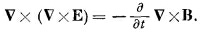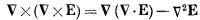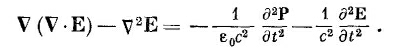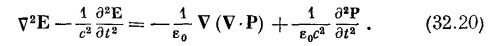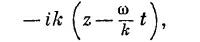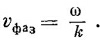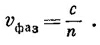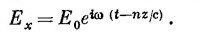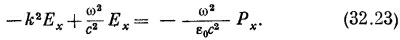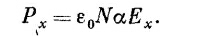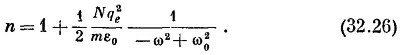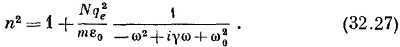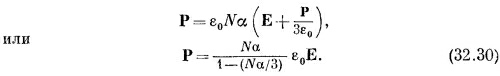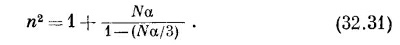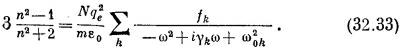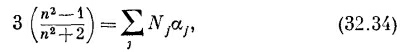Главная >> Фейнмановские лекции по физике >> Том 7 >> Глава 32. Показатель преломления плотного вещества

Волны в диэлектрике

Теперь нам предстоит выяснить, какого сорта электромагнитные волны могут существовать в диэлектрическом веществе, где других зарядов, кроме тех, что связаны в атомах, нет. Таким образом, мы возьмем ρ = –V·P и j = ∂P/∂t. При этом уравнения Максвелла примут такой вид:

Мы можем решить эти уравнения, как делали это прежде. Начнем с применения к уравнению (32.19в) операции ротора:

Используя затем векторное тождество

и подставляя выражение для VxB из (32.19б), получаем

Используя уравнение (32.19а) для V·E, находим

Таким образом, вместо волнового уравнения мы теперь получили, что даламбертиан Е равен двум членам, содержащим поляризацию Р.
 
Однако Р зависит от Е, поэтому уравнение (32.20) все еще допускает волновые решения. Сейчас мы будем ограничиваться изотропными диэлектриками, т. е. Р всегда будет иметь то же направление, что и Е. Попробуем найти решение для волны, движущейся в направлении оси z. Электрическое поле при этом будет изменяться как e^¡(ωt–kz). Предположим также, что волна поляризована в направлении оси х, т. е. что электрическое поле имеет только x-компоненту. Все это записывается следующим образом:

Вы знаете, что любая функция от (z—vt) представляет волну, бегущую со скоростью v. Показатель экспоненты в выражении (32.21) можно переписать в виде

так что выражение (32.21) представляет волну, фазовая скорость которой равна

В гл. 31 (вып. 3) показатель преломления n определялся нами из формулы

С учетом этой формулы (32.21) приобретает вид

Таким образом, показатель n можно определить, если мы найдем ту величину k, которая необходима, чтобы выражение (32.21) удовлетворяло соответствующим уравнениям поля, и затем воспользуемся соотношением

В изотропном материале поляризация будет иметь только x-компоненту; кроме того, Р не изменяется с изменением координаты х, поэтому V·P=0 и мы сразу же избавляемся от первого члена в правой стороне уравнения (32.20). Вдобавок мы считаем наш диэлектрик «линейным», поэтому Р_х будет изменяться как е^¡ωt и ∂²P_x/∂t² = –ω²Р_x. Лапласиан же в уравнении (32.20) превращается просто в ∂²E_x/∂z²= –к²Е_х, так что в результате получаем

Теперь на минуту предположим, что раз Е изменяется синусоидально, то Р можно считать пропорциональной Е, как в уравнении (32.5). (Позднее мы вернемся к этому предположению и обсудим его.) Таким образом, пишем

При этом Е_х выпадает из уравнения (32.23), и мы находим

Мы получили, что волна вида (32.21) с волновым числом к, задаваемым уравнением (32.24), будет удовлетворять уравнениям поля. Использование же выражения (32.22) для показателя n дает

Сравним эту формулу с тем, что получилось у нас для показателя преломления газа (гл. 31, вып. 3). Там мы нашли уравнение (31.19), которое тогда имело вид

Формула (32.25) после подстановки α из (32.6) дает

Что здесь нового? Во-первых, появился новый член ¡γω, возникший в результате учета поглощения энергии в осцилляторах. Во-вторых, слева вместо n теперь стоит n² и, кроме того, отсутствует дополнительный множитель ¹/₂. Но заметьте, что если значение N достаточно мало, так что n близок к единице (как это имеет место в газе), то выражение (32.27) говорит,что n² равен единице плюс некое малое число, т. е. n²=1+ε. При этом условии мы можем написать, что n=√1+ε ≈1+ ε/2, и оба выражения оказываются эквивалентными. Таким образом, наш новый метод дает для газа тот же самый, найденный нами ранее результат.
 
Теперь можно надеяться, что выражение (32.27) должно давать показатель преломления и для плотных материалов. Но по некоторым причинам оно нуждается в модификации. Во-первых, при выводе этого уравнения предполагалось, что поляризованное поле, действующее на каждый из атомов,— это поле Е_х. Однако такое предположение неверно, поскольку в плотном материале существуют и другие поля, создаваемые соседними атомами, которые могут быть сравнимы с Е_х. Аналогичную задачу мы уже рассматривали при изучении статических полей в диэлектрике (см. гл. 11, вып. 5). Вы, вероятно, помните, что мы нашли поле, действующее на отдельный атом; представив его сидящим в сферической полости в окружающем диэлектрике. Поле в такой полости (мы назвали его локальным) увеличивается по сравнению со средним полем Е на величину Р/Зε₀. (Не забудьте, однако, что этот результат, строго говоря, справедлив только для изотропного материала, а также в случае кубического кристалла.)
 
Те же рассуждения верны и для электрического поля в волне, но до тех пор, пока длина ее много больше расстояния между атомами. При таком ограничении

Именно это локальное поле следует использовать вместо Е в (32.8), т. е. это выражение должно быть переписано следующим образом:

Подставляя теперь Е_лок из формулы (32.28), находим

Иными словами, Р для плотного материала все еще пропорциональна Е (для синусоидального поля). Однако константа пропорциональности будет уже ε₀Nα/ [1 — (Nα/З)], а не ε₀Nα, как раньше. Таким образом, нам нужно поправить формулу (32.25):

Более удобно переписать это в виде

который алгебраически эквивалентен прежнему. Это и есть известная формула Клаузиуса — Моссотти.
 
В плотном материале возникает и другое усложнение. Поскольку атомы расположены слишком тесно, они сильно взаимодействуют друг с другом. Поэтому внутренние гармоники осцилляции изменяются. Собственные частоты атомных осцилляции размазываются этими взаимодействиями и обычно весьма сильно подавляются ими, а коэффициент трения становится очень большим. Таким образом, все ω_о и γ твердого вещества будут другими, чем для свободных атомов. С этой оговоркой мы все-таки можем представлять α, по крайней мере приближенно, уравнением (32.7), так что

Наконец, последнее усложнение. Если плотный материал представляет собой смесь нескольких компонент, то каждая из них дает свой вклад в поляризацию. Полная α будет суммой вкладов различных компонент смеси [за исключением неточности приближения локального поля в упорядоченных кристаллах, т. е. выражения (32.28) —эффекты, которые мы обсуждали при разборе сегнетоэлектриков]. Обозначая через N_j число атомов каждой компоненты в единице объема, мы должны заменить формулу (32.32) следующей:

где каждая α_j- будет определяться выражением типа (32.7). Выражение (32.34) завершает нашу теорию показателя преломления. Величина 3(n²–1)/(n²+2) задается комплексной функцией частоты, каковой является средняя атомная поляризуемость α(ω). Точное вычисление α(ω) (т. е. нахождение f_k, γ_k и ω_ok) для плотного вещества — одна из труднейших задач квантовой механики. Это было сделано только для нескольких особенно простых веществ.

СМОТРИТЕ ТАКЖЕ: