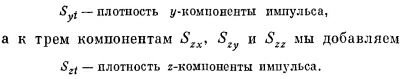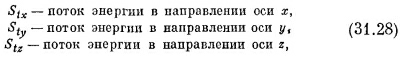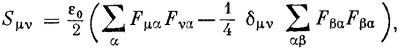Главная >> Фейнмановские лекции по физике >> Том 7 >> Глава 31. Тензоры

Четырехмерный тензор электромагнитного импульса

Все тензоры, с которыми мы сталкивались в этой главе, были связаны с трехмерным пространством; они определялись как величины, имеющие известные трансформационные свойства при пространственных поворотах. А вот в гл. 26 (вып. 6) мы имели возможность воспользоваться тензором в четырехмерном пространстве-времени: это был тензор электромагнитного поля F_μv . Компоненты такого четырехмерного тензора особым образом преобразуются при преобразованиях Лоренца. (Мы этого, правда, не делали, но могли бы рассматривать преобразования Лоренца как своего рода «вращение» в четырехмерном «пространстве», называемом пространством Минковского; тогда аналогия с тем, что мы рассматривали здесь, была бы ярче.)
 
В качестве последнего примера мы хотим рассмотреть другой тензор в четырех измерениях (t, х,у, z) теории относительности. Когда мы говорили о тензоре напряжений, то определяли S_¡j как компоненту силы, действующую на единичную площадку. Но сила равна скорости изменения импульса со временем. Поэтому вместо того, чтобы говорить «S_xy — это х-компонента силы, действующей на единичную площадку, перпендикулярную оси у», мы с равным правом могли бы сказать: S_xy — это скорость потока x-компоненты импульса через единичную площадку, перпендикулярную оси у». Другими словами, каждый член S_¡j представляет поток ¡-й компоненты импульса через единичную площадку, перпендикулярную оси j. Так обстоит дело с чисто пространственными компонентами, но они составляют только часть «большего» тензора S_μv в четырехмерном пространстве (μ и v=t, x, у, z), содержащего еще дополнительные компоненты S_tx , S_yt , S_tt и т. п. Попытаемся теперь выяснить физический смысл этих дополнительных компонент.
 
Нам известно, что пространственные компоненты представляют поток импульса. Чтобы найти ключ к распространению этого понятия на «временное направление», обратимся к «потоку» другого рода — потоку электрического заряда. Скорость потока скалярной величины, подобной заряду (через единичную площадь, перпендикулярную потоку), является пространственным вектором — вектором плотности тока j. Мы видели, что временная компонента вектора потока — это плотность текущего вещества. Например, j можно скомбинировать с плотностью заряда j_t=ρ и получить четырехвектор j_μ= (ρ, j), т. е. значок μ у вектора j_μ принимает четыре значения: t, x, у, z. Это означает «плотность», «скорость потока в x-направлении», «скорость потока в y-направлении» и «скорость потока в z-направлении» скалярного заряда.
 
Теперь по аналогии с нашим утверждением о временной компоненте потока скалярной величины можно ожидать, что вместе S_xx,S_xy и S_xz, описывающими поток х-компоненты импульса, должна быть и временная компонента S_xt, которая по идее должна бы описывать плотность того, что течет, т. е. S_xt должна быть плотностью x-компоненты импульса. Таким образом, мы можем расширить наш тензор по горизонтали, включив в него t-компоненты, и в нашем распоряжении оказываются:

Аналогичная вещь происходит и с y-компонентой; у нас есть три компоненты потока: S_yx , S_yy и S_yz , к которым нужно добавить четвертый член:

В четырехмерном пространстве у импульса существует также и t-компонента, которой, как мы знаем, является энергия. Так что тензор S_ij следует продолжить по вертикали с включением в него S_tx, S_ty и S_tz, причем

т. е. S_tx— это поток энергии в единицу времени через поверхность единичной площади, перпендикулярную оси х, и т. д. Наконец, чтобы пополнить наш тензор, нужна еще величина S_tt, которая должна быть плотностью энергии. Итак, мы расширили наш трехмерный тензор напряжений до четырехмерного тензора энергии-импульса S_μv. Индекс μ может принимать четыре значения: t, х, у и z, которые означают «плотность», «поток через единичную площадь в направлении оси х», «поток через единичную площадь в направлении оси у» и «поток через единичную площадь в направлении оси z». Значок v тоже принимает четыре значения: t, x, у, z, которые говорят нам, что же именно течет: «энергия», «x-компонента импульса», «y-компонента импульса» или же «z-компонента импульса».
 
В качестве примера рассмотрим этот тензор не в веществе, а в пустом пространстве с электромагнитным полем. Вы знаете, что поток энергии электромагнитного поля описывается вектором Пойнтинга S=ε₀c²E xB. Так что х-, у- и z-компоненты вектора S с релятивистской точки зрения являются компонентами S_tx, S_ty  и S_tz нашего тензора энергии-импульса. Симметрия тензора S¡j переносится и на временные компоненты, так что четырехмерный тензор S_μv   тоже симметричен:

Другими словами, компоненты S_xt , S_yt , S _zt , которые представляют плотности х-, у- и z-компонент импульса, равны также х-, у- и z-компонентам вектора Пойнтинга S, или, как мы видели раньше из других соображений, вектора потока энергии.
 
Оставшиеся компоненты тензора электромагнитного напряжения S_μv тоже можно выразить через электрическое и магнитное поля Е и В. Иначе говоря, для электромагнитного поля в пустом пространстве мы должны допустить существование тензора напряжений, или, выражаясь менее таинственно, потока импульса электромагнитного поля. Мы уже обсуждали это в гл. 27 (вып. 6) в связи с уравнением (27.21), но тогда мы не входили в детали.
 
Тем из вас, кто хочет испытать свою удаль на четырехмерных тензорах, может понравиться выражение для тензора S_μv через поля:

где суммирование по α и β проводится по всем их значениям (т. е. t, х, у и z), но, как обычно в теории относительности, для суммы ∑ и символа δ принимается специальное соглашение. В суммах слагаемые со значками х, у, z должны вычитаться, а δ_tt=+1, тогда как б_xx = б_уу=б_zz= –1 и δ_μv=0 для всех μ≠v (с=1). Сможете ли вы доказать, что эта формула приводит к плотности энергии S_tt=(ε₀/2)(E²+B²) и вектору Пойнтинга ε₀Е хВ? Можете ли вы показать, что в электростатическом поле, когда В = 0, главная ось напряжения направлена по электрическому полю и вдоль направления поля возникает натяжение (ε₀ /2)Е² и равное ему давление в направлении, перпендикулярном направлению поля?

СМОТРИТЕ ТАКЖЕ: