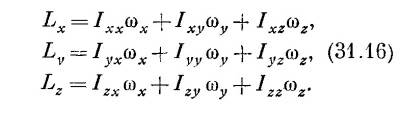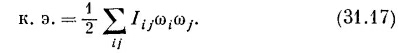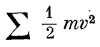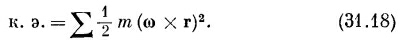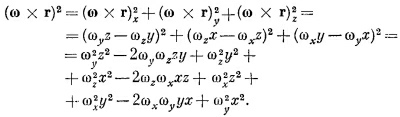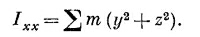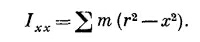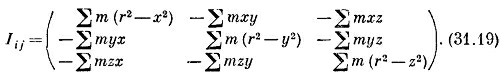| Обучение и материалы |
|---|
| Физический справочник |
| Формулы по физике |
| Шпаргалки по физике |
| Энциклопедия |
| Репетиторы по физике |
| Работа для физиков |
| Быстрый устный счет |
| Виртуальные лабораторные |
| Опыты по физике |
| ЕГЭ онлайн |
| Онлайн тестирование |
| Ученые физики |
| Необъяснимые явления |
| Ваша реклама на сайте |
| Разное |
| Контакты |
| Спецкурс |
|---|
| Фейнмановские лекции |
|
В мире больших скоростей |
Введение в теорию относительности |
|
Лекции по биофизике |
| Лекции по ядерной физике |
| Ускорение времени... |
| Лазеры |
| Нанотехнологии |
| Книги |
| полезное |
|---|
| Смешные анекдоты о физике
Готовые шпоры по физике Физика в жизни Ученые и деньги Нобелевские лауреаты Фото Видео Карта сайта |
| На заметку |
|---|
| Если вам понравился сайт, предлагаем разместить нашу кнопку |
| Дополнительно |
|---|
|
Компьютерные программы по физике 
Физика и юмор 
Онлайн тестирование по физике 
|
Другие тензоры. Тензор инерции
В физике есть еще немало других примеров тензоров. В металле, например, или каком-либо другом проводнике зачастую оказывается, что плотность тока j приблизительно пропорциональна электрическому полю Е, причем константа пропорциональности называется проводимостью σ:
Однако для кристалла соотношение между j и Е более сложно, проводимость в различных направлениях не одинакова. Она становится тензором, поэтому мы пишем
Другим примером физического тензора является момент инерции. В гл. 18 (вып. 2) мы видели, что момент количества движения L твердого тела, вращающегося относительно фиксированной оси, пропорционален угловой скорости ω, и коэффициент пропорциональности / мы назвали моментом инерции:
Девять коэффициентов I¡j называют тензором инерции. По аналогии с поляризацией кинетическая энергия для любого момента количества движения должна быть некоторой квадратичной формой компонент ωх, ωy и ωz:
Мы можем снова воспользоваться этим выражением для определения эллипсоида инерции. Кроме того, снова можно воспользоваться энергетическими соображениями и показать, что этот тензор симметричен, т. е. /¡j= /j¡.
по всем частицам тела. Но скорость v каждой частицы связана с угловой скоростью ω твердого тела. Предположим, что тело вращается относительно центра масс, который мы будем считать покоящимся. Если при этом r — положение частицы относительно центра масс, то ее скорость v задается выражением ωX r. Поэтому полная кинетическая энергия равна
Единственное, что нужно теперь сделать,— это переписать ω х r через компоненты ωх, ωy, ωz и координаты х, у, z, а затем сравнить результат с уравнением (31.17); приравнивая коэффициенты, найдем I¡j. Проделывая всю эту алгебру, мы пишем:
Умножая это уравнение на т/2, суммируя по всем частицам и сравнивая с уравнением (31.17), мы видим, что Iхх, например, равно
Это и есть та формула для момента инерции тела относительно оси х, которую мы получали уже раньше (гл. 19, вып. 2). Ну а поскольку r2 = x2 + y2+z2, то эту же формулу можно написать в виде
Выписав остальные члены тензора инерции, получим
Если хотите, его можно записать в «тензорных обозначениях»:
где через r¡ обозначены компоненты (х, у, z) вектора положения частицы, а ∑ означает суммирование по всем частицам. Таким образом, момент инерции есть тензор второго ранга, элементы которого определяются свойствами тела и который связывает момент количества движения L с угловой скоростью ω:
Для любого тела независимо от его формы можно найти эллипсоид энергии, а следовательно, и три главные оси. Относительно этих осей тензор будет диагональным, так что для любого объекта всегда есть три ортогональные оси, для которых момент количества движения и угловая скорость параллельны друг другу. Они называются главными осями инерции. СМОТРИТЕ ТАКЖЕ:Социальные комментарии Cackle |
© All-Физика, 2009-2026
При использовании материалов сайта ссылка на www.all-fizika.com обязательна.
При использовании материалов сайта ссылка на www.all-fizika.com обязательна.

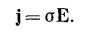
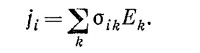
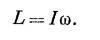
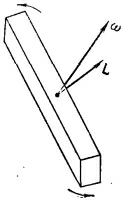 Момент инерции тела произвольной формы зависит от его ориентации относительно оси вращения. Моменты инерции прямоугольного бруска, например, относительно каждой из трех ортогональных осей будут разными. Но угловая скорость ω и момент количества движения L — оба векторы. Для вращения относительно одной из осей симметрии они параллельны. Но если моменты инерции относительно каждой из трех главных осей различны, то направления ω и L, вообще говоря, не совпадают (фиг. 31.4). Они связаны точно таким же образом, как Е и Р, т. е. мы должны писать:
Момент инерции тела произвольной формы зависит от его ориентации относительно оси вращения. Моменты инерции прямоугольного бруска, например, относительно каждой из трех ортогональных осей будут разными. Но угловая скорость ω и момент количества движения L — оба векторы. Для вращения относительно одной из осей симметрии они параллельны. Но если моменты инерции относительно каждой из трех главных осей различны, то направления ω и L, вообще говоря, не совпадают (фиг. 31.4). Они связаны точно таким же образом, как Е и Р, т. е. мы должны писать: