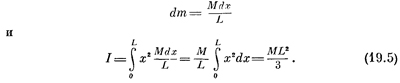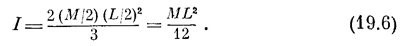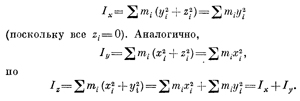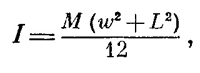| Обучение и материалы |
|---|
| Физический справочник |
| Формулы по физике |
| Шпаргалки по физике |
| Энциклопедия |
| Репетиторы по физике |
| Работа для физиков |
| Быстрый устный счет |
| Виртуальные лабораторные |
| Опыты по физике |
| ЕГЭ онлайн |
| Онлайн тестирование |
| Ученые физики |
| Необъяснимые явления |
| Ваша реклама на сайте |
| Разное |
| Контакты |
| Спецкурс |
|---|
| Фейнмановские лекции |
|
В мире больших скоростей |
Введение в теорию относительности |
|
Лекции по биофизике |
| Лекции по ядерной физике |
| Ускорение времени... |
| Лазеры |
| Нанотехнологии |
| Книги |
| полезное |
|---|
| Смешные анекдоты о физике
Готовые шпоры по физике Физика в жизни Ученые и деньги Нобелевские лауреаты Фото Видео Карта сайта |
| На заметку |
|---|
| Если вам понравился сайт, предлагаем разместить нашу кнопку |
| Дополнительно |
|---|
|
Компьютерные программы по физике 
Физика и юмор 
Онлайн тестирование по физике 
|
Вычисление момента инерции
Рассмотрим теперь проблему определения момента инерции различных тел. Общая формула для нахождения момента инерции объекта относительно оси z имеет вид
Иными словами, нужно сложить все массы, умножив каждую из них на квадрат ее расстояния до оси (x2i + y2i). Заметьте, что это верно даже для трехмерного тела, несмотря на то, что расстояние имеет такой «двумерный вид». Впрочем, в большинстве случаев мы будем ограничиваться двумерными телами.
Размерность момента инерции всегда равна массе, умноженной на квадрат длины, так что единственная существенная величина, которую мы вычислили, это множитель 1/3. А чему будет равен момент инерции I, если ось вращения проходит через середину стержня? Чтобы найти его, нам снова нужно взять интеграл, но уже в пределах от —1/2L до +1/2L. Заметим, однако, одну особенность этого случая. Такой стержень с проходящей через центр осью можно представлять себе как два стержня с осью, проходящей через конец, причем масса каждого из них равна М/2, а длина равна L/2. Моменты инерции двух таких стержней равны друг другу и вычисляются по формуле (19.5). Поэтому момент инерции всего стержня равен
Таким образом, стержень гораздо легче крутить за середину, чем за конец. Можно, конечно, продолжить вычисление моментов инерции других интересующих нас тел. Но поскольку такие расчеты требуют большого опыта в вычислении интегралов (что очень важно само по себе), они как таковые не представляют для нас большого интереса. Впрочем, здесь имеются некоторые очень интересные и полезные теоремы. Пусть имеется какое-то тело и мы хотим узнать его момент инерции относительно какой-то оси. Это означает, что мы хотим найти его инертность при вращении вокруг этой оси. Если мы будем двигать тело за стержень, подпирающий его центр масс так, чтобы оно не поворачивалось при вращении вокруг оси (в этом случае на него не действуют никакие моменты сил инерции, поэтому тело не будет поворачиваться, когда мы начнем двигать его), то для того, чтобы повернуть его, понадобится точно такая же сила, как если бы вся масса была сосредоточена в центре масс и момент инерции был бы просто равен I1 = MR2ц.м., где Rц.м — расстояние от центра масс до оси вращения. Однако формула эта, разумеется, неверна. Она не дает правильного момента инерции тела. Ведь в действительности при повороте тело вращается. Крутится не только центр масс (что давало бы величину I1), само тело тоже должно поворачиваться относительно центра масс. Таким образом, к моменту инерции I1 нужно добавить Iц — момент инерции относительно центра масс. Правильный ответ состоит в том, что момент инерции относительно любой оси равен
Эта теорема называется теоремой о параллельном переносе оси. Доказывается она очень легко. Момент инерции относительно любой оси равен сумме масс, умноженных на сумму квадратов х и у, т. е. I = Σmi(x2i + y2i). Мы сейчас сосредоточим наше внимание на х, однако все в точности можно повторить и для у. Пусть координата х есть расстояние данной частной точки от начала координат; посмотрим, однако, как все изменится, если мы будем измерять расстояние х` от центра масс вместо х от начала координат. Чтобы это выяснить, мы должны написать Что получится, если умножить его на mi и просуммировать по всем r? Вынося постоянные величины за знак суммирования, находим Ix = Σmix`2i + 2Xц.м.Σmix`i + X2ц.м.Σmi Третью сумму подсчитать легко; это просто МХ2ц.м. . Второй член состоит из двух сомножителей, один из которых Σmix`i; он равен x`-координате центра масс. Но это должно быть равно нулю, ведь х` отсчитывается от центра масс, а в этой системе координат среднее положение всех частиц, взвешенное их массами, равно нулю. Первый же член, очевидно, представляет собой часть х от Iц. Таким образом, мы и приходим к формуле (19.7). Давайте проверим формулу (19.7) на одном примере. Просто проверим, будет ли она применима для стержня. Мы уже нашли, что момент инерции стержня относительно его конца должен быть равен ML2/3. А центр масс стержня, разумеется, находится на расстоянии L/2. Таким образом, мы должны получить, что ML2/3=ML2/12+M(L/2)2. Так как одна четвертая + одна двенадцатая = одной третьей, то мы не сделали никакой грубой ошибки. Кстати, чтобы найти момент инерции (19.5), вовсе не обязательно вычислять интеграл. Можно просто предположить, что он равен величине ML2, умноженной на некоторый неизвестный коэффициент γ. После этого можно использовать рассуждения о двух половинках и для момента инерции (19.6) получить коэффициент 1/4γ. Используя теперь теорему о параллельном переносе оси, докажем, что γ=1/4γ + 1/4, откуда γ=1/3. Всегда можно найти какой-нибудь окольный путь! При применении теоремы о параллельных осях важно помнить, что ось Iц должна быть параллельна оси, относительно которой мы хотим вычислять момент инерции. Стоит, пожалуй, упомянуть еще об одном свойстве, которое часто бывает очень полезно при нахождении момента инерции некоторых типов тел. Оно состоит в следующем: если у нас есть плоская фигура и тройка координатных осей с началом координат, расположенным в этой плоскости, и осью z, направленной перпендикулярно к ней, то момент инерции этой фигуры относительно оси z равен сумме моментов инерции относительно осей х и у. Доказывается это совсем просто. Заметим, что
Момент инерции однородной прямоугольной пластинки, например с массой М, шириной ω и длиной L относительно оси, перпендикулярной к ней и проходящей через ее центр, равен просто
поскольку момент инерции относительно оси, лежащей в плоскости пластинки и параллельной ее длине, равен Mω2/12, т. е. точно такой же, как и для стержня длиной ω, а момент инерции относительно другой оси в той же плоскости равен ML2/12, такой же, как и для стержня длиной L. Итак, перечислим свойства момента инерции относительно данной оси, которую мы назовем осью z: 1. Момент инерции равен
2. Если предмет состоит из нескольких частей, причем момент инерции каждой из них известен, то полный момент инерции равен сумме моментов инерции этих частей.
В табл. 19.1 приведены моменты инерции некоторых элементарных фигур, имеющих однородную плотность масс, а в табл. 19.2 — моменты инерции некоторых фигур, которые могут быть получены из табл. 19.1 с использованием перечисленных выше свойств.
СМОТРИТЕ ТАКЖЕ:Социальные комментарии Cackle |
При использовании материалов сайта ссылка на www.all-fizika.com обязательна.

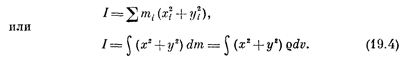
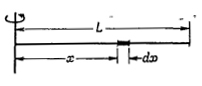 В качестве простого примера рассмотрим стержень, вращающийся относительно оси, проходящей через его конец и перпендикулярной к нему (фиг. 19.3). Нам нужно просуммировать теперь все массы, умноженные на квадраты расстояния х (в этом случае все у — нулевые). Под суммой, разумеется, я имею в виду интеграл от х2, умноженный на «элементики» массы. Если мы разделим стержень на кусочки длиной dx, то соответствующий элемент массы будет пропорционален dx, а если бы dx составляло длину всего стержня, то его масса была бы равна М. Поэтому
В качестве простого примера рассмотрим стержень, вращающийся относительно оси, проходящей через его конец и перпендикулярной к нему (фиг. 19.3). Нам нужно просуммировать теперь все массы, умноженные на квадраты расстояния х (в этом случае все у — нулевые). Под суммой, разумеется, я имею в виду интеграл от х2, умноженный на «элементики» массы. Если мы разделим стержень на кусочки длиной dx, то соответствующий элемент массы будет пропорционален dx, а если бы dx составляло длину всего стержня, то его масса была бы равна М. Поэтому