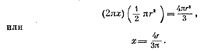| Обучение и материалы |
|---|
| Физический справочник |
| Формулы по физике |
| Шпаргалки по физике |
| Энциклопедия |
| Репетиторы по физике |
| Работа для физиков |
| Быстрый устный счет |
| Виртуальные лабораторные |
| Опыты по физике |
| ЕГЭ онлайн |
| Онлайн тестирование |
| Ученые физики |
| Необъяснимые явления |
| Ваша реклама на сайте |
| Разное |
| Контакты |
| Спецкурс |
|---|
| Фейнмановские лекции |
|
В мире больших скоростей |
Введение в теорию относительности |
|
Лекции по биофизике |
| Лекции по ядерной физике |
| Ускорение времени... |
| Лазеры |
| Нанотехнологии |
| Книги |
| полезное |
|---|
| Смешные анекдоты о физике
Готовые шпоры по физике Физика в жизни Ученые и деньги Нобелевские лауреаты Фото Видео Карта сайта |
| На заметку |
|---|
| Если вам понравился сайт, предлагаем разместить нашу кнопку |
| Дополнительно |
|---|
|
Компьютерные программы по физике 
Физика и юмор 
Онлайн тестирование по физике 
|
Положение центра масс
Математическая техника вычисления центра масс относится к области курсов математики; там подобные задачи служат хорошими примерами по интегральному исчислению. Но, даже умея интегрировать, полезно знать некоторые трюки для вычисления положения центра масс. Один из таких трюков основан на использовании так называемой теоремы Паппа, которая работает следующим образом. Если мы возьмем какую-то замкнутую фигуру и образуем твердое тело, вращая эту фигуру в пространстве так, чтобы каждая точка двигалась перпендикулярно к плоскости фигуры, то объем образующегося при этом тела равен произведению площади фигуры на расстояние, пройденное ее центром тяжести! Разумеется, эта теорема верна и в том случае, когда плоская фигура движется по прямой линии, перпендикулярной к ее площади, однако если мы движем ее по окружности или какой-то другой кривой, то при этом получается гораздо более интересное тело. При движении по кривому пути внутренняя часть фигуры продвигается меньше, чем внешняя, и эти эффекты компенсируют друг друга. Так что если мы хотим определить центр масс плоской фигуры с однородной плотностью, то нужно помнить, что объем, образуемый вращением его относительно оси, равен расстоянию, которое проходит центр масс, умноженному на площадь фигуры.
Как это увидеть? Рассеките треугольник линиями, параллельными основанию, на множество полосок. Заметьте теперь, что медиана делит каждую полоску пополам, следовательно, центр масс должен лежать на медиане. Возьмем теперь более сложную фигуру. Предположим, что требуется найти положение центра масс однородного полукруга, т. е. круга, разрезанного пополам. Где будет находиться центр масс в этом случае? Для полного круга центр масс расположен в геометрическом центре, но для полукруга найти его положение труднее. Пусть r— радиус круга, а х — расстояние центра масс от прямолинейной границы полукруга. Вращая его вокруг этого края как вокруг оси, мы получаем шар. При этом центр масс проходит расстояние 2πх, а площадь полукруга равна 1/2πr2 (половине площади круга). Так как объем шара равен, конечно, 4πr3/3, то отсюда находим
Существует еще другая теорема Паппа, которая фактически является частным случаем сформулированной выше теоремы, а потому тоже справедлива. Предположим, что вместо твердого полукруга мы взяли полуокружность, например кусок проволоки в виде полуокружности с однородной плотностью, и хотим найти ее центр масс. Оказывается, что площадь, которая «заметается» плоской кривой при ее движении, аналогичном вышеописанному, равна расстоянию, пройденному центром масс, умноженному на длину этой кривой. (Кривую можно рассматривать как очень узкую полоску и применять к ней предыдущую теорему.) СМОТРИТЕ ТАКЖЕ:Социальные комментарии Cackle |
© All-Физика, 2009-2026
При использовании материалов сайта ссылка на www.all-fizika.com обязательна.
При использовании материалов сайта ссылка на www.all-fizika.com обязательна.

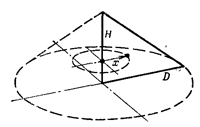 Например, если нам нужно найти центр масс прямоугольного треугольника с основанием D и высотой Н (фиг. 19.2), то это делается следующим образом. Вообразите себе ось, проходящую вдоль Н, и поверните треугольник на 360° вокруг этой оси. Это дает нам конус. Расстояние, которое проходит ж-координата центра масс, равно 2πx, а площадь области, которая двигалась, т. е. площадь треугольника, равна 1/2HD. Произведение расстояния, пройденного центром масс, на площадь треугольника равно объему конуса, т. е. 1/3πD2H. Таким образом, (2πx)(1/2HD)=1/3πD2H, или x=D/3. Совершенно аналогично вращением вокруг второго катета или просто по соображениям симметрии находим, что у=Н/3. Вообще центр масс любого однородного треугольника находится в точке пересечения трех его медиан (линий, соединяющих вершину треугольника с серединой противоположной стороны), которая отстоит от основания на расстоянии, равном х/3 длины каждой медианы.
Например, если нам нужно найти центр масс прямоугольного треугольника с основанием D и высотой Н (фиг. 19.2), то это делается следующим образом. Вообразите себе ось, проходящую вдоль Н, и поверните треугольник на 360° вокруг этой оси. Это дает нам конус. Расстояние, которое проходит ж-координата центра масс, равно 2πx, а площадь области, которая двигалась, т. е. площадь треугольника, равна 1/2HD. Произведение расстояния, пройденного центром масс, на площадь треугольника равно объему конуса, т. е. 1/3πD2H. Таким образом, (2πx)(1/2HD)=1/3πD2H, или x=D/3. Совершенно аналогично вращением вокруг второго катета или просто по соображениям симметрии находим, что у=Н/3. Вообще центр масс любого однородного треугольника находится в точке пересечения трех его медиан (линий, соединяющих вершину треугольника с серединой противоположной стороны), которая отстоит от основания на расстоянии, равном х/3 длины каждой медианы.