| Обучение и материалы |
|---|
| Физический справочник |
| Формулы по физике |
| Шпаргалки по физике |
| Энциклопедия |
| Репетиторы по физике |
| Работа для физиков |
| Быстрый устный счет |
| Виртуальные лабораторные |
| Опыты по физике |
| ЕГЭ онлайн |
| Онлайн тестирование |
| Ученые физики |
| Необъяснимые явления |
| Ваша реклама на сайте |
| Разное |
| Контакты |
| Спецкурс |
|---|
| Фейнмановские лекции |
|
В мире больших скоростей |
Введение в теорию относительности |
|
Лекции по биофизике |
| Лекции по ядерной физике |
| Ускорение времени... |
| Лазеры |
| Нанотехнологии |
| Книги |
| полезное |
|---|
| Смешные анекдоты о физике
Готовые шпоры по физике Физика в жизни Ученые и деньги Нобелевские лауреаты Фото Видео Карта сайта |
| На заметку |
|---|
| Если вам понравился сайт, предлагаем разместить нашу кнопку |
| Дополнительно |
|---|
|
Компьютерные программы по физике 
Физика и юмор 
Онлайн тестирование по физике 
|
Геометрия пространства-времени
Теория относительности показывает, что связь между местоположением события и моментом, в какой оно происходит, при измерениях в двух разных системах отсчета совсем не такая, как можно было ожидать на основе наших интуитивных представлений. Очень важно ясно представить себе связь пространства и времени, возникающую из преобразований Лоренца. Поэтому мы глубже рассмотрим этот вопрос. Координаты и время (х, у, z, t), измеренные «покоящимся» наблюдателем, преобразуются в координаты и время (х`, у`, z`, t`), измеренные внутри «движущегося» со скоростью и космического корабля:
Давайте сравним эти уравнения с уравнением (11.5); которое тоже связывает измерения в двух системах, только одна из них теперь вращается относительно другой
В этом частном случае у Мика и Джо оси х` и х повернуты на угол θ. Но и в том и в другом случае мы замечаем, что «штрихованные» величины — это «перемешанные» между собой «нештрихованные»: новое х` есть смесь х и у, а новое у` — другая смесь х и у. Проведем следующую аналогию: когда мы глядим на предмет, мы различаем его «видимую ширину» и «видимую толщину». Но эти два понятия — «ширина» и «толщина» — отнюдь не основные свойства предмета. Отойдите в сторону, взгляните на предмет под другим углом — видимая ширина и видимая толщина предмета станут другими. Можно написать формулы, позволяющие узнать новые ширину и толщину по известным старым и по углу поворота. Уравнения (17.2) — как раз эти формулы. Можно сказать, что данная толщина есть своего рода «смесь» всех ширин и всех толщин. Если б мы не могли сдвинуться с места, если б мы на данный предмет всегда глядели из одного и того же положения, то нам все эти рассуждения показались бы неуместными; мы ведь и так всегда видели бы пред собой «настоящую» ширину и «настоящую» толщину и знали бы, что это совершенно разные качества предмета: один связан с углом, под каким виден предмет, другой требует фокусирования глаза и даже интуиции. Они казались бы абсолютно различными, их незачем было бы смешивать. Только потому, что мы в состоянии обойти вокруг предмета, мы понимаем, что ширина и толщина — это разные стороны одного и того же предмета. Нельзя ли взглянуть на преобразование Лоренца таким же способом! Ведь и здесь перед нами смесь — смесь местоположения и момента времени. Из значений координаты и времени получается новая координата. Иначе говоря, в измерениях пространства, сделанных одним человеком, есть с точки зрения другого малая примесь времени. Наша аналогия позволяет высказать следующую мысль: «реальность» предмета, на который мы смотрим, включает нечто большее (говоря грубо и образно), чем его «ширину» и его «толщину», потому что обе они зависят от того, как мы смотрим на предмет. Оказавшись на новом месте, наш мозг немедленно пересчитывает и ширину, и толщину. Но когда мы будем двигаться с большой скоростью, наш мозг не сможет немедленно пересчитать координаты и время: у нас нет опыта движений со скоростями, близкими к световой, мы не ощущаем время и пространство как явления одной природы. Все равно как если бы нас усадили на какое-то место, заставили бы разглядывать ширину какого-то предмета и при этом не разрешали бы даже поворачивать голову. Мы теперь понимаем, что, будь у нас такая возможность, мы могли бы увидеть немножко от времени другого человека, как бы «заглянуть» сзади него.
А как обстоит дело со светом? Скорость света всегда одна и та же, значит, свет можно изображать прямыми линиями одинакового наклона (d на фиг. 17.1).
СМОТРИТЕ ТАКЖЕ:Социальные комментарии Cackle |
При использовании материалов сайта ссылка на www.all-fizika.com обязательна.

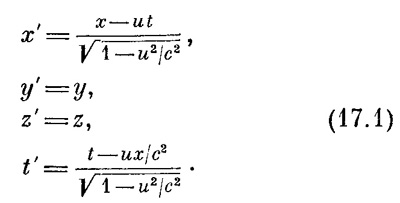
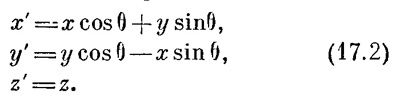
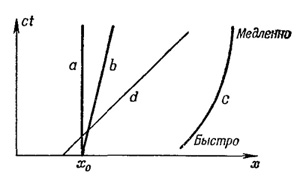 Итак, мы должны попытаться представить себе предметы в мире нового типа, в котором время с пространством смешано в том же смысле, в каком предметы нашего привычного пространственного мира можно разглядывать с разных направлений. Мы должны считать, что предметы, занимающие некоторое место и существующие некоторый период времени, занимают некую «дольку» мира нового типа и что мы смотрим на эту «дольку» с разных точек зрения, когда движемся с разной скоростью. Этот новый мир, эта геометрическая реальность, в которой имеются «дольки», занимающие некоторое пространство и существующие некоторое время, называется пространством-временем. Данная точка (х, у, z, t) в пространстве-времени носит название события. Представьте, например, что ось х мы поместили горизонтально, оси у и z — в двух других направлениях, взаимно перпендикулярных и перпендикулярных к странице (!), а ось t направили вертикально. Как на такой диаграмме изобразится, скажем, движущаяся частица? Когда частица неподвижна, у нее есть какая-то координата х; время течет, а х остается все тем же, и тем же, и тем же. Значит, ее «путь» — это прямая, параллельная оси (а на фиг. 17.1). С другой стороны, если она равномерно удаляется, то с течением времени растет и х (b на фиг. 17.1). Таким образом, частица, которая сперва двигалась, а потом стала замедлять свой ход, изобразится чем-то похожим на кривую с на фиг. 17.1. Другими словами, всякая устойчивая, нераспадающаяся частица изображается линией в пространстве-времени. А распадающаяся частица изобразится вилкой, потому что она превращается в две частицы, выходящие из одной точки.
Итак, мы должны попытаться представить себе предметы в мире нового типа, в котором время с пространством смешано в том же смысле, в каком предметы нашего привычного пространственного мира можно разглядывать с разных направлений. Мы должны считать, что предметы, занимающие некоторое место и существующие некоторый период времени, занимают некую «дольку» мира нового типа и что мы смотрим на эту «дольку» с разных точек зрения, когда движемся с разной скоростью. Этот новый мир, эта геометрическая реальность, в которой имеются «дольки», занимающие некоторое пространство и существующие некоторое время, называется пространством-временем. Данная точка (х, у, z, t) в пространстве-времени носит название события. Представьте, например, что ось х мы поместили горизонтально, оси у и z — в двух других направлениях, взаимно перпендикулярных и перпендикулярных к странице (!), а ось t направили вертикально. Как на такой диаграмме изобразится, скажем, движущаяся частица? Когда частица неподвижна, у нее есть какая-то координата х; время течет, а х остается все тем же, и тем же, и тем же. Значит, ее «путь» — это прямая, параллельная оси (а на фиг. 17.1). С другой стороны, если она равномерно удаляется, то с течением времени растет и х (b на фиг. 17.1). Таким образом, частица, которая сперва двигалась, а потом стала замедлять свой ход, изобразится чем-то похожим на кривую с на фиг. 17.1. Другими словами, всякая устойчивая, нераспадающаяся частица изображается линией в пространстве-времени. А распадающаяся частица изобразится вилкой, потому что она превращается в две частицы, выходящие из одной точки.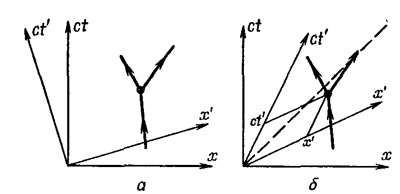 Итак, согласно высказанной нами идее, если происходит некое событие, например частица внезапно распадается в какой-то пространственно-временной точке (х, t) на две, то, если это для чего-нибудь нужно, поворотом осей можно получить значения х и t в новой системе (фиг. 17.2, а). Но это не так: ведь уравнение (17.1) не совпадает с преобразованием (17.2), в них по-разному расставлены знаки, в одном встречаются sin θ и cos θ, а в другом — некоторые алгебраические величины. (Вообще-то иногда алгебраические величины выражаются через косинус и синус, но в данном случае это невозможно.) А все-таки эти выражения очень похожи. Как мы с вами увидим, нельзя представлять себе пространство-время в виде реальной обычной геометрии, и все из-за этой разницы в знаках. На самом деле, хотя мы этого пока не подчеркивали, оказывается, что движущийся наблюдатель должен пользоваться осями, равнонаклоненными к линии светового луча, и проектировать точку на эти оси при помощи отрезков, им параллельных. Это показано на фиг. 17.2, б. Мы не будем заниматься этой геометрией, она не особенно помогает; легче работать прямо с уравнениями.
Итак, согласно высказанной нами идее, если происходит некое событие, например частица внезапно распадается в какой-то пространственно-временной точке (х, t) на две, то, если это для чего-нибудь нужно, поворотом осей можно получить значения х и t в новой системе (фиг. 17.2, а). Но это не так: ведь уравнение (17.1) не совпадает с преобразованием (17.2), в них по-разному расставлены знаки, в одном встречаются sin θ и cos θ, а в другом — некоторые алгебраические величины. (Вообще-то иногда алгебраические величины выражаются через косинус и синус, но в данном случае это невозможно.) А все-таки эти выражения очень похожи. Как мы с вами увидим, нельзя представлять себе пространство-время в виде реальной обычной геометрии, и все из-за этой разницы в знаках. На самом деле, хотя мы этого пока не подчеркивали, оказывается, что движущийся наблюдатель должен пользоваться осями, равнонаклоненными к линии светового луча, и проектировать точку на эти оси при помощи отрезков, им параллельных. Это показано на фиг. 17.2, б. Мы не будем заниматься этой геометрией, она не особенно помогает; легче работать прямо с уравнениями.