| Обучение и материалы |
|---|
| Физический справочник |
| Формулы по физике |
| Шпаргалки по физике |
| Энциклопедия |
| Репетиторы по физике |
| Работа для физиков |
| Быстрый устный счет |
| Виртуальные лабораторные |
| Опыты по физике |
| ЕГЭ онлайн |
| Онлайн тестирование |
| Ученые физики |
| Необъяснимые явления |
| Ваша реклама на сайте |
| Разное |
| Контакты |
| Спецкурс |
|---|
| Фейнмановские лекции |
|
В мире больших скоростей |
Введение в теорию относительности |
|
Лекции по биофизике |
| Лекции по ядерной физике |
| Ускорение времени... |
| Лазеры |
| Нанотехнологии |
| Книги |
| полезное |
|---|
| Смешные анекдоты о физике
Готовые шпоры по физике Физика в жизни Ученые и деньги Нобелевские лауреаты Фото Видео Карта сайта |
| На заметку |
|---|
| Если вам понравился сайт, предлагаем разместить нашу кнопку |
| Дополнительно |
|---|
|
Компьютерные программы по физике 
Физика и юмор 
Онлайн тестирование по физике 
|
Преобразование скоростей
Главное отличие принципа относительности Эйнштейна от принципа относительности Ньютона заключается в том, что законы преобразований, связывающих координаты и времена в системах, движущихся относительно друг друга, различны. Правильный закон преобразований (Лоренца) таков:
Эти уравнения отвечают сравнительно простому случаю, когда наблюдатели движутся относительно друг друга вдоль общей оси х. Конечно, мыслимы и другие направления движения, но самое общее преобразование Лоренца выглядит довольно сложно: в нем перемешаны все четыре числа. Мы и впредь будем пользоваться этой простой формулой, так как она содержит в себе все существенные черты теории относительности. Рассмотрим теперь дальнейшие следствия этого преобразования. Прежде всего интересно разрешить эти уравнения относительно х, у, z, t. Это система четырех линейных уравнений для четырех неизвестных, и их можно решить — выразить х, у, z, t через х`, у`, z`, t`. Результат этот потому интересен, что он говорит нам, как «покоящаяся» система координат выглядит с точки зрения «движущейся». Ясно, что из-за относительности движения и постоянства скорости тот, кто «движется», может, если пожелает, счесть себя неподвижным, другого — движущимся. А поскольку он движется в обратную сторону, то получит то же преобразование, но с противоположным знаком у скорости. Это в точности то, что дает и прямое решение системы, так что все сходится. Вот если бы не сошлось, было бы от чего встревожиться!
Теперь займемся интересным вопросом о сложении скоростей в теории относительности. Напомним, что первоначально загадка состояла в том, что свет проходит 300 000 км/сек во всех системах, даже если они движутся друг относительно друга. Это — частный случай более общей задачи. Приведем пример. Пусть предмет внутри космического корабля движется вперед со скоростью 200 000 км/сек; скорость самого корабля тоже 200 000 км/сек. С какой скоростью перемещается предмет с точки зрения внешнего наблюдателя? Хочется сказать: 400 000 км/сек, но эта цифра уж больно подозрительна: получается скорость большая, чем скорость света! Разве можно себе это представить? Общая постановка задачи такова. Пусть скорость тела внутри корабля равна v (с точки зрения наблюдателя на корабле), а сам корабль имеет скорость и по отношению к Земле. Мы желаем знать, с какой скоростью vx это тело движется с точки зрения земного наблюдателя. Впрочем, это тоже не самый общий случай, потому что движение происходит в направлении х. Могут быть формулы для преобразования скоростей в направлении у или в любом другом; если они будут нужны, их всегда можно вывести. Внутри корабля скорость тела равна vx`. Это значит, что перемещение х` равно скорости, умноженной на время:
Остается только подсчитать, какие у тела значения х и t с точки зрения внешнего наблюдателя, если х` и t` связаны соотношением (16.3). Подставим (16.3) в (16.2) и получим Но здесь х выражено через t`. А скорость с точки зрения внешнего наблюдателя — это «его» расстояние, деленное на «его» время, а не на время другого наблюдателях Значит, надо и время подсчитать с его позиций
А теперь разделим х на t. Квадратные корни сократятся, останется же
Это и есть искомый закон: суммарная скорость не равна сумме скоростей (это привело бы ко всяким несообразностям), но «подправлена» знаменателем 1 + uv/c2. Что же теперь будет получаться? Пусть ваша скорость внутри корабля равна половине скорости света, а скорость корабля тоже равна половине скорости света. Значит, и uравно 1/2c, и v равно 1/2с, но в знаменателе uv равно 1/4, так что
Выходит по теории относительности, что 1/2 и 1/2 дают не 1 а 4/5. Небольшие скорости, конечно, можно складывать, как обычно, потому что, пока скорости по сравнению со скоростью света малы, о знаменателе (1 + uv/c2) можно забыть, но на больших скоростях положение меняется. Возьмем предельный случай. Положим, что человек на борту корабля наблюдает, как распространяется свет. Тогда v=c. Что обнаружит земной наблюдатель? Ответ будет такой:
Значит, если что-то движется со скоростью света внутри корабля, то, с точки зрения стороннего наблюдателя, скорость не изменится, она по-прежнему будет равна скорости света! Это именно то, ради чего в первую очередь предназначал Эйнштейн свою теорию относительности. Конечно, бывает, что движение тела не совпадает по направлению с равномерным движением корабля. Например, тело движется «вверх» со скоростью гу по отношению к кораблю, а корабль движется «горизонтально». Проделывая такие же манипуляции (только х надо заменить на у), получаем
СМОТРИТЕ ТАКЖЕ:Социальные комментарии Cackle |
При использовании материалов сайта ссылка на www.all-fizika.com обязательна.

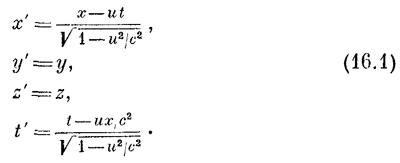
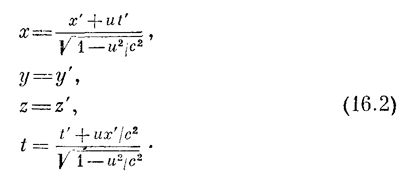

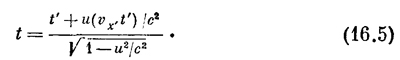
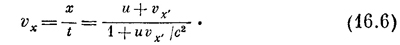
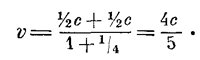
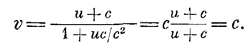
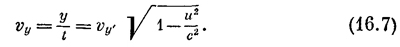
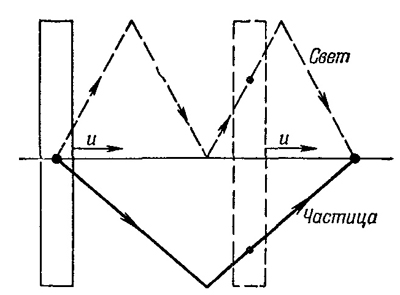 Итак, боковая скорость тела уже не vy`, a vy`√(1-u2/c2). Этот результат мы получили, пользуясь формулами преобразований. Но он вытекает и прямо из принципа относительности по следующей причине (всегда бывает полезно докопаться до первоначальной причины). Мы уже раньше рассуждали (см. фиг. 15.3) о том, как могут работать движущиеся часы; свет кажется распространяющимся наискось со скоростью с в неподвижной системе, в то время как в движущейся системе он просто движется вертикально с той же скоростью. Мы нашли, что вертикальная компонента скорости в неподвижной системе меньше скорости света на множитель √(1-u2/c2) [см. уравнение (15.3)]. Пусть теперь материальная частица движется в тех же «часах» взад-вперед со скоростью, равной 1/п скорости света (фиг. 16.1). Пока частица пройдет туда и обратно, свет пройдет этот путь ровно n раз (n — целое число). Значит, каждое тиканье «часов с частицей» совпадет с n-м тиканьем «световых часов». Этот факт должен остаться верным и тогда, когда тело движется, потому что физическое явление совпадения остается совпадением в любой системе. Ну а поскольку скорость су меньше скорости света, то скорость vy частицы должна быть меньше соответствующей скорости в том же отношении (с квадратным корнем)! Вот почему в любой вертикальной скорости появляется корень.
Итак, боковая скорость тела уже не vy`, a vy`√(1-u2/c2). Этот результат мы получили, пользуясь формулами преобразований. Но он вытекает и прямо из принципа относительности по следующей причине (всегда бывает полезно докопаться до первоначальной причины). Мы уже раньше рассуждали (см. фиг. 15.3) о том, как могут работать движущиеся часы; свет кажется распространяющимся наискось со скоростью с в неподвижной системе, в то время как в движущейся системе он просто движется вертикально с той же скоростью. Мы нашли, что вертикальная компонента скорости в неподвижной системе меньше скорости света на множитель √(1-u2/c2) [см. уравнение (15.3)]. Пусть теперь материальная частица движется в тех же «часах» взад-вперед со скоростью, равной 1/п скорости света (фиг. 16.1). Пока частица пройдет туда и обратно, свет пройдет этот путь ровно n раз (n — целое число). Значит, каждое тиканье «часов с частицей» совпадет с n-м тиканьем «световых часов». Этот факт должен остаться верным и тогда, когда тело движется, потому что физическое явление совпадения остается совпадением в любой системе. Ну а поскольку скорость су меньше скорости света, то скорость vy частицы должна быть меньше соответствующей скорости в том же отношении (с квадратным корнем)! Вот почему в любой вертикальной скорости появляется корень.