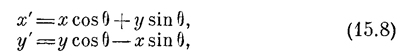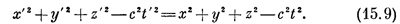| Обучение и материалы |
|---|
| Физический справочник |
| Формулы по физике |
| Шпаргалки по физике |
| Энциклопедия |
| Репетиторы по физике |
| Работа для физиков |
| Быстрый устный счет |
| Виртуальные лабораторные |
| Опыты по физике |
| ЕГЭ онлайн |
| Онлайн тестирование |
| Ученые физики |
| Необъяснимые явления |
| Ваша реклама на сайте |
| Разное |
| Контакты |
| Спецкурс |
|---|
| Фейнмановские лекции |
|
В мире больших скоростей |
Введение в теорию относительности |
|
Лекции по биофизике |
| Лекции по ядерной физике |
| Ускорение времени... |
| Лазеры |
| Нанотехнологии |
| Книги |
| полезное |
|---|
| Смешные анекдоты о физике
Готовые шпоры по физике Физика в жизни Ученые и деньги Нобелевские лауреаты Фото Видео Карта сайта |
| На заметку |
|---|
| Если вам понравился сайт, предлагаем разместить нашу кнопку |
| Дополнительно |
|---|
|
Компьютерные программы по физике 
Физика и юмор 
Онлайн тестирование по физике 
|
Четырехвекторы
Что еще можно обнаружить в преобразованиях Лоренца? Любопытно, что в них преобразование х и t по форме похоже на преобразование х и у, изученное нами в гл. 11, когда мы говорили о вращении координат. Тогда мы получили
т. е. новое х перемешивает старые х и y, а у` тоже их перемешивает. Подобным же образом в преобразовании Лоренца новое х` есть смесь старых х и t, а новое t` — смесь t и х. Значит, преобразование Лоренца похоже на вращение, но «вращение» в пространстве и времени. Это весьма странное понятие. Проверить аналогию с вращением можно, вычислив величину
В этом уравнении три первых члена в каждой стороне представляют собой в трехмерной геометрии квадрат расстояния между точкой и началом координат (сферу). Он не меняется (остается инвариантным), несмотря на вращение осей координат. Аналогично, уравнение (15.9) свидетельствует о том, что существует определенная комбинация координат и времени, которая остается инвариантной при преобразовании Лоренца. Значит, имеется полная аналогия с вращением; аналогия эта такого рода, что векторы, т. е. величины, составленные из «компонент», преобразуемых так же, как и координаты, оказываются полезными и в теории относительности. Итак, мы расширим понятие вектора. Пока он у нас мог иметь только пространственные компоненты. Теперь включим в это понятие и временную компоненту, т. е. мы ожидаем, что существуют векторы с четырьмя компонентами: три из них похожи на компоненты обычного вектора, а к ним привязана четвертая — аналог времени. В следующих главах мы проанализируем это понятие. Мы увидим, что если идеи этого параграфа приложить к импульсу, то преобразование даст три пространственные составляющие, подобные обычным компонентам .импульса, и четвертую компоненту — временную часть (которая есть не что иное, как энергия). СМОТРИТЕ ТАКЖЕ:Социальные комментарии Cackle |
© All-Физика, 2009-2026
При использовании материалов сайта ссылка на www.all-fizika.com обязательна.
При использовании материалов сайта ссылка на www.all-fizika.com обязательна.