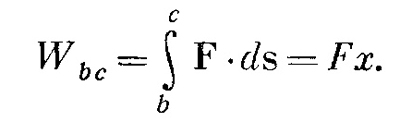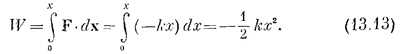| Обучение и материалы |
|---|
| Физический справочник |
| Формулы по физике |
| Шпаргалки по физике |
| Энциклопедия |
| Репетиторы по физике |
| Работа для физиков |
| Быстрый устный счет |
| Виртуальные лабораторные |
| Опыты по физике |
| ЕГЭ онлайн |
| Онлайн тестирование |
| Ученые физики |
| Необъяснимые явления |
| Ваша реклама на сайте |
| Разное |
| Контакты |
| Спецкурс |
|---|
| Фейнмановские лекции |
|
В мире больших скоростей |
Введение в теорию относительности |
|
Лекции по биофизике |
| Лекции по ядерной физике |
| Ускорение времени... |
| Лазеры |
| Нанотехнологии |
| Книги |
| полезное |
|---|
| Смешные анекдоты о физике
Готовые шпоры по физике Физика в жизни Ученые и деньги Нобелевские лауреаты Фото Видео Карта сайта |
| На заметку |
|---|
| Если вам понравился сайт, предлагаем разместить нашу кнопку |
| Дополнительно |
|---|
|
Компьютерные программы по физике 
Физика и юмор 
Онлайн тестирование по физике 
|
Работа, выполняемая тяжестью
Теперь займемся задачей потруднее, когда силы уже не постоянны и не направлены вниз, как раньше. Мы рассмотрим, например, движение планеты вокруг Солнца или спутника вокруг Земли.
Этот одномерный случай рассматривать легко, потому что мы знаем, что изменение кинетической энергии равно интегралу от начала движения до конца от силы —GMm/r2 по перемещению dr
В формуле нет никакого косинуса, потому что сила и перемещение направлены одинаково.Интегрировать dr/r2 легко; получается (—1/r), так что
Перед нами другая формула для потенциальной энергии. Уравнение (13.12) говорит нам, что величина 1/2mv2— GMm/r, вычисленная в точке 1, в точке 2 или в любой другой, остается постоянной.
От 2 до 3 сила в точности направлена поперек движения, и W23=0. От 3 к 4
Так же получаются W45 =0, W56 = — GMm(1/r6— 1/r5), W67=0, W78= — GMm(1/r8— 1/r7) и W81=0. Всего
Но ведь r2 = r3, r4 = r5, r6 = r7, r8 = r1. Поэтому W=0.
(поскольку сила постоянна). Теперь определим работу на двух катетах. На вертикальном катете аЬ сила перпендикулярна к ds, так что работа равна нулю. На горизонтальном катете bc
Мы убеждаемся таким образом, что работа обхода по бокам маленького треугольника такая же, как и по склону, потому что s cos θ равно х. Мы уже показали прежде, что работа при движении по зазубринам (как на фиг. 13.3) равна нулю, а теперь видим, что производимая работа одинакова, независимо от того, движемся ли мы по зазубринам или срезаем путь между ними (если только зазубрины малы, но ведь ничто не мешает сделать их такими); поэтому работа обхода по любому замкнутому пути в поле тяготения равна нулю. Это очень примечательный результат. Благодаря ему нам становятся известны такие подробности о движении планет, о которых мы раньше и не догадывались. Выясняется, что когда планета вертится вокруг Солнца одна, без спутников и в отсутствие каких-либо других сил, то квадрат ее скорости минус некоторая константа, деленная на расстояние до Солнца, вдоль орбиты не меняется. Например, чем ближе планета к Солнцу, тем быстрее она движется. Но насколько быстрее? А вот насколько: если вместо движения вокруг Солнца вы толкнете ее к Солнцу с той же скоростью и подождете, пока она не упадет на нужное расстояние, то приобретенная скорость будет как раз такой, какой планета обладает на этой орбите, потому что получился просто другой пример сложного пути обхода. Если планета вернется по такому пути обратно, ее кинетическая энергия окажется прежней. Поэтому независимо от того, движется ли она по настоящей невозмущенной орбите или же по сложному пути (но без трения), кинетическая энергия в момент возвращения на орбиту оказывается как раз такой, какой нужно. Значит, когда мы проводим численный анализ движения планеты но орбите (как мы делали раньше), мы можем проверить, не сделали ли заметных ошибок при расчете этой постоянной величины, энергии, на каждом шаге; она не должна меняться. Для орбиты, приведенной в табл. 9.2, энергия меняется примерно на 1,5% с начала движения до конца. Почему? То ли потому, что в численном методе мы пользовались конечными приращениями, то ли из-за мелких погрешностей в арифметике. Рассмотрим энергию в другой задаче: задаче о массе, подвешенпой на пружине. Когда отклоняют массу от положения равновесия, сила, восстанавливающая ее положение, пропорциональна смещению. Можно ли в этих условиях вывести закон сохранения оперши? Да; потому что работа, совершаемая этой силой, равна
Значит, у массы, подвешенной на пружине, сумма кинетической энергии ее колебаний и 1/2kx2 постоянна. Посмотрим, как это происходит. Оттянем массу вниз; она неподвижна и скорость ее равна нулю, но х не равно нулю, теперь величина х максимальна, так что имеется и некоторый запас энергии (потенциальной). Отпустим теперь массу: начнется какой-то процесс (в детали мы не вникаем), но в любое мгновение кинетическая плюс потенциальная энергии будут постоянны. Например, когда масса проходит через точку первоначального равновесия, то х=0, но тогда значение v2 наибольшее, и чем больше величина х1, тем меньше v2 и т. д. Значит, во время колебаний соблюдается равновесие между величинами х2 и v2. Мы получили, таким образом, новое правило: потенциальная энергия пружины равна 1/2kx2, если сила равна — kх. СМОТРИТЕ ТАКЖЕ:Социальные комментарии Cackle |
При использовании материалов сайта ссылка на www.all-fizika.com обязательна.

 Сперва мы рассмотрим движение тела, которое падает из точки 1 прямо на Солнце или на Землю (фиг. 13.2). Будет ли в этих обстоятельствах сохраняться энергия? Единственное отличие от того, что было раньше, — что теперь сила не постоянна, она меняется по мере падения. Мы знаем, что сила равна произведению GM/r2 на массу т. падающего тела. Конечно, и теперь кинетическая энергия при падении возрастает, как возрастала и тогда, когда нас еще не волновало изменение силы с высотой. Вопрос только в том, можно ли отыскать иную, отличную от mgh, формулу для потенциальной энергии, найти другую функцию расстояния от Земли, чтобы для нее сохранение энергии не нарушалось.
Сперва мы рассмотрим движение тела, которое падает из точки 1 прямо на Солнце или на Землю (фиг. 13.2). Будет ли в этих обстоятельствах сохраняться энергия? Единственное отличие от того, что было раньше, — что теперь сила не постоянна, она меняется по мере падения. Мы знаем, что сила равна произведению GM/r2 на массу т. падающего тела. Конечно, и теперь кинетическая энергия при падении возрастает, как возрастала и тогда, когда нас еще не волновало изменение силы с высотой. Вопрос только в том, можно ли отыскать иную, отличную от mgh, формулу для потенциальной энергии, найти другую функцию расстояния от Земли, чтобы для нее сохранение энергии не нарушалось.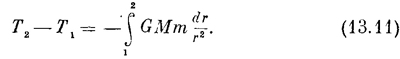
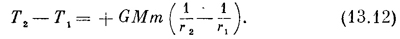
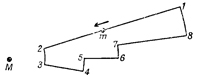 У нас теперь есть формула для потенциальной энергии в поле тяготения для вертикального движения. Здесь возникает интересный вопрос: можно ли добиться вечного движения в поле тяготения? Поле-то меняется, в разных местах у него разная напряженность и разное направление. Нельзя ли взять бесконечную ленту без трения и запустить ее, скажем, так: пусть она сперва поднимает тело из одной точки в другую, потом прово дит его по дуге окружности в третью точку, опускает на некоторый уровень, сдвигает по наклонному направлению и выводит на новый путь и т. п., так что по возвращении в начальную точку оказывается, что поле тяготения совершило некоторую работу и кинетическая энергия тела возросла? Нельзя ли так начертить эту траекторию, чтобы, обойдя по ней, тело приобрело чуть-чуть больше скорости, чем имело вначале? Так получится вечное движение. Но ведь оно невозможно, значит, мы обязаны доказать, что такая траектория немыслима. Мы должны доказать следующее предположение: раз трения нет, тело должно вернуться ни с меньшей, ни с большей скоростью, а как раз с такой, чтобы еще и еще делать круги по этому замкнутому пути. Или, другими словами, вся работа, произведенная в движении по замкнутому пути, должна быть нулем для сил тяжести, потому что если бы она не была нулем, то можно было бы получить энергию за счет такого движения тела. (Если бы работа оказалась меньше нуля, так что скорость в конце обхода уменьшилась бы, то для получения энергии стоило бы только повернуть обратно; силы ведь зависят не от направления движения, а только от положения. Если в одном направлении работа получится с плюсом, то в обратном она будет с минусом; любая ненулевая работа означает создание вечного двигателя.) Так что же, действительно ли работа равна нулю? Попробуем показать, что да. Сперва мы лишь на пальцах поясним, почему это так, а уж потом оформим математически. Положим, мы выдумали траекторию, показанную на фиг. 13.3; масса падает от 1 к 2, поворачивает до 3, обратно поднимается к 4, затем через 5, 6, 7, 8 движется обратно к 1. Все линии идут либо по радиусу, либо по кругу с центром М. Какая работа совершается на таком пути? Между 1 и 2 она равна произведению GMm на разность 1/r в этих точках:
У нас теперь есть формула для потенциальной энергии в поле тяготения для вертикального движения. Здесь возникает интересный вопрос: можно ли добиться вечного движения в поле тяготения? Поле-то меняется, в разных местах у него разная напряженность и разное направление. Нельзя ли взять бесконечную ленту без трения и запустить ее, скажем, так: пусть она сперва поднимает тело из одной точки в другую, потом прово дит его по дуге окружности в третью точку, опускает на некоторый уровень, сдвигает по наклонному направлению и выводит на новый путь и т. п., так что по возвращении в начальную точку оказывается, что поле тяготения совершило некоторую работу и кинетическая энергия тела возросла? Нельзя ли так начертить эту траекторию, чтобы, обойдя по ней, тело приобрело чуть-чуть больше скорости, чем имело вначале? Так получится вечное движение. Но ведь оно невозможно, значит, мы обязаны доказать, что такая траектория немыслима. Мы должны доказать следующее предположение: раз трения нет, тело должно вернуться ни с меньшей, ни с большей скоростью, а как раз с такой, чтобы еще и еще делать круги по этому замкнутому пути. Или, другими словами, вся работа, произведенная в движении по замкнутому пути, должна быть нулем для сил тяжести, потому что если бы она не была нулем, то можно было бы получить энергию за счет такого движения тела. (Если бы работа оказалась меньше нуля, так что скорость в конце обхода уменьшилась бы, то для получения энергии стоило бы только повернуть обратно; силы ведь зависят не от направления движения, а только от положения. Если в одном направлении работа получится с плюсом, то в обратном она будет с минусом; любая ненулевая работа означает создание вечного двигателя.) Так что же, действительно ли работа равна нулю? Попробуем показать, что да. Сперва мы лишь на пальцах поясним, почему это так, а уж потом оформим математически. Положим, мы выдумали траекторию, показанную на фиг. 13.3; масса падает от 1 к 2, поворачивает до 3, обратно поднимается к 4, затем через 5, 6, 7, 8 движется обратно к 1. Все линии идут либо по радиусу, либо по кругу с центром М. Какая работа совершается на таком пути? Между 1 и 2 она равна произведению GMm на разность 1/r в этих точках: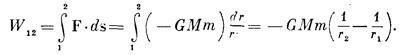
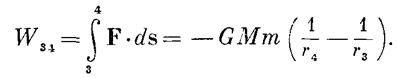
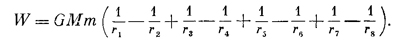
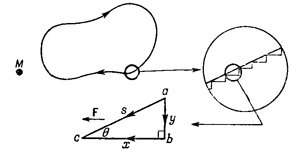 Но возникает подозрение, не слишком ли эта кривая проста. А что даст настоящая траектория? Что ж, попробуем настоящую. Сразу же ясно, что ее можно достаточно точно представить как ряд зазубрин (фиг. 13.4) и поэтому... и т. д., что и требовалось доказать. Но надо еще посмотреть, действительно ли работа обхода вокруг маленького треугольника тоже равна нулю. Увеличим один из треугольников (см. фиг. 13.4). Равны ли работы по пути от а к b и от b к c работе, совершаемой, когда идешь напрямик от а к с? Пусть сила действует в каком-то направлении. Расположим треугольник так, чтобы у его катета bc было как раз такое направление. Предположим также, что сам треугольник так мал, что сила всюду на нем постоянна. Какова работа на отрезке ас? Она равна
Но возникает подозрение, не слишком ли эта кривая проста. А что даст настоящая траектория? Что ж, попробуем настоящую. Сразу же ясно, что ее можно достаточно точно представить как ряд зазубрин (фиг. 13.4) и поэтому... и т. д., что и требовалось доказать. Но надо еще посмотреть, действительно ли работа обхода вокруг маленького треугольника тоже равна нулю. Увеличим один из треугольников (см. фиг. 13.4). Равны ли работы по пути от а к b и от b к c работе, совершаемой, когда идешь напрямик от а к с? Пусть сила действует в каком-то направлении. Расположим треугольник так, чтобы у его катета bc было как раз такое направление. Предположим также, что сам треугольник так мал, что сила всюду на нем постоянна. Какова работа на отрезке ас? Она равна