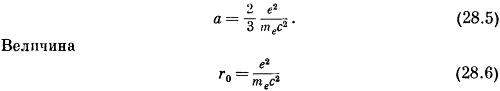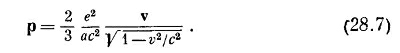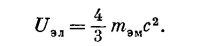Главная >> Фейнмановские лекции по физике >> Том 6 >> Глава 28. Электромагнитная масса

Электромагнитная масса

Откуда же вообще возникло понятие массы? В наших законах механики мы предполагали, что любому предмету присуще некое свойство, называемое массой. Оно означает пропорциональность импульса предмета его скорости. Теперь же мы обнаружили, что это свойство вполне понятно — заряженная частица несет импульс, который пропорционален ее скорости. Дело можно представить так, как будто масса — это просто электродинамический эффект. Ведь до сих пор причина возникновения массы оставалась нераскрытой. И вот, наконец, в электродинамике нам представилась прекрасная возможность понять то, чего мы никогда не понимали раньше. Прямо как с неба (а точнее, от Максвелла и Пойнтинга) свалилось на нас объяснение пропорциональности импульса любой заряженной частицы ее скорости через электромагнитные свойства.
 
Но давайте все-таки встанем на более консервативную точку зрения и будем говорить, по крайней мере временно, что имеется два сорта масс и что полный импульс предмета должен быть суммой механического и электромагнитного импульсов. Причем механический импульс равен произведению «механической» массы m_мех на скорость v. В тех экспериментах, где масса частицы измеряется, например, определением импульса или «кручением на веревочке», мы находим ее полную массу. Импульс равен произведению именно полной массы (m_мex+m_эм) на скорость. Таким образом, наблюдаемая масса может состоять из двух (а может быть, и из большего числа, если мы учтем другие поля) частей: механической и электромагнитной. Мы знаем, что наверняка имеется электромагнитная часть; для нее у нас есть даже формула. А сейчас появилась увлекательная возможность выбросить механическую массу совсем и считать массу полностью электромагнитной.
 
Посмотрим, каков должен быть размер электрона, если «механическая» часть массы полностью отсутствует. Это можно выяснить, приравнивая электромагнитную массу (28.4) наблюдаемой массе электрона, т. е. т_е. Получаем

называется  «классическим радиусом электрона»   и равна   она 2,82х10^–13 см, т. е. одной стотысячной диаметра атома.
 
Почему радиусом электрона названа величина r₀, а не а? Потому что мы можем провести те же самые расчеты с другим распределением заряда. Мы можем взять его равномерно размазанным по всему объему шара или наподобие пушистого шарика. Например, для заряда, равномерно распределенного по всему объему сферы, коэффициент ²/з заменяется коэффициентом ⁴/₅. Вместо того чтобы спорить, какое распределение правильно, а какое нет, было решено взять в качестве «номинального» радиуса величину r₀. А разные теории приписывают к ней свой коэффициент.
 
Давайте продолжим наше обсуждение электромагнитной теории массы. Мы провели расчет для v «c с, а что произойдет при переходе к большим скоростям? Первые попытки вычисления привели к какой-то путанице, но позднее Лоренц понял, что при больших скоростях заряженная сфера должна сжиматься в эллипсоид, а поля должны изменяться согласно полученным нами для релятивистского случая в гл. 26 формулам (26.6) и (26.7). Если вы проделаете все вычисления для р в этом случае, то получите, что для произвольной скорости v импульс умножается еще на 1/√1—v²/c², т. е.

Другими словами, электромагнитная масса возрастает с увеличением скорости обратно пропорционально √1−v²lc². Это открытие было сделано еще до создания теории относительности.
 
Тогда предлагались даже эксперименты по определению зависимости наблюдаемой массы от скорости, чтобы установить, какая часть ее электрическая по своему происхождению, а какая — механическая. В те времена считали, что электромагнитная часть массы должна зависеть от скорости, а ее механическая часть — нет.
 
Но пока ставились эксперименты, теоретики тоже не дремали. И вскоре была развита теория относительности, которая доказала, что любая масса, независимо от своего происхождения, должна изменяться как т₀/√1–v²lc². Таким образом, уравнение (28.7) было началом теории, согласно которой масса зависит от скорости.
 
А теперь вернемся к нашим вычислениям энергии поля, которые привели к выводу выражения (28.2). Энергия U в соответствии с теорией относительности эквивалентна массе U/с², поэтому (28.2) говорит, что поле электрона должно обладать массой

которая не совпадает с электромагнитной массой т_эм, определенной формулой  (28.4).   В  самом деле,  если бы  мы  просто скомбинировали выражения  (28.2)  и  (28.4), то должны  были бы написать

Эта формула была получена еще до теории относительности, и когда Эйнштейн и другие физики начали понимать, что U всегда должно быть равно тс², то замешательство было очень велико.

СМОТРИТЕ ТАКЖЕ: