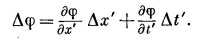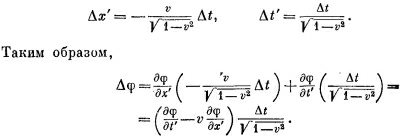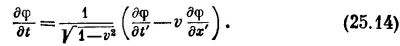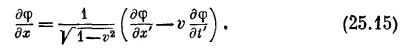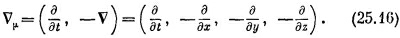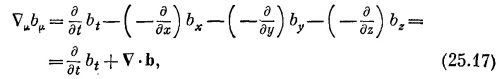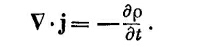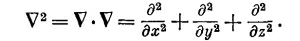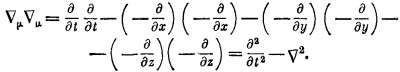Главная >> Фейнмановские лекции по физике >> Том 6 >> Глава 25. Электродинамика в релятивистских обозначениях

Четырехмерный градиент

Следующей величиной, которую нам следует обсудить, является четырехмерный аналог градиента. Напомним (см. гл. 14, вып. 1), что три оператора дифференцирования д/дх, д/ду, д/дz преобразуются подобно трехмерному вектору и называются градиентом. Та же схема должна работать и в четырех измерениях; по простоте вы можете подумать, что четырехмерным градиентом должны быть (д/дt, д/дх, д/ду д/дz), но это неверно.
 
Чтобы обнаружить ошибку, рассмотрим скалярную функцию, которая зависит только от х и t. Приращение φ при малом изменении t на Δt и постоянном х равно

С другой  стороны,  с точки  зрения  движущегося  наблюдателя

Используя уравнение (25.1), мы можем выразить Δх′ и Δt′ через Δt. Вспоминая теперь, что величина х постоянна, так что Δх = 0, мы пишем

Сравнивая этот результат с (25.13), мы узнаем, что

Аналогичные вычисления дают

Теперь вы видите, что градиент получился довольно странным. Выражения для х и t через х′ и t′ [полученные решением уравнений (25.1)] имеют вид

Именно так должен   преобразовываться  четырехвектор. Но в уравнениях (25.14) и (25.15) знаки получились неправильными! Выход в том, что надо заменить неправильное определение четырехмерного оператора градиента (∂/∂t, v) правильным:

Мы его обозначим v_μ . Для такого v_μ трудности исчезают, и он ведет себя так, как подобает настоящему четырехвектору. (Ужасно неприятно наличие минусов, но так уж устроено в мире.) Разумеется, говоря, что v_μ «ведет себя как четырехвектор», мы подразумеваем, что четырехмерный градиент скалярной функции есть четырехвектор. Если φ — настоящее скалярное (лоренц-инвариантное) поле, то v_μφ будет четырехвекторным полем.
 
Итак, все уладилось. Теперь у нас есть векторы, градиенты и скалярное произведение. Следующий на очереди — инвариант, аналогичный дивергенции в трехмерном векторном анализе. Ясно, что аналогом его должно быть выражение v_μb_μ , где b_μ — векторное поле, компоненты которого являются функциями пространства и времени. Мы определим дивергенцию четырехвектора b_μ =(b_t, b) как скалярное произведение v_μ  на b_μ :

где v·b — обычная трехмерная дивергенция вектора b. Не забывайте внимательно следить за знаками. Один знак минус связан с определением скалярного произведения [формула (25.7)], а другой возникает от пространственных компонент v_μ [формула (25.16)]. Дивергенция, определяемая формулой (25.7), есть инвариант, и для всех систем координат, отличающихся друг от друга преобразованием Лоренца, применение ее приводит к одинаковой величине.
 
Остановимся теперь на физическом примере, в котором появляется четырехмерная дивергенция. Ею можно воспользоваться при решении задачи о полях вокруг движущегося проводника. Мы уже видели (гл. 13, § 7, вып. 5), что плотность электрического заряда ρ и плотность тока j образуют четырехвектор j_μ=(ρ, j). Если незаряженный провод переносит ток j_х, то в системе отсчета, движущейся относительно него со скоростью v (вдоль оси х), в проводнике наряду с током появится и заряд [который возникает  согласно   закону  преобразований Лоренца (25.1)]:

Но это как раз то, что мы нашли в гл. 13. Теперь нужно подставить эти источники в уравнение Максвелла в движущейся системе и найти поля.
 
Закон сохранения заряда в четырехмерных обозначениях тоже принимает очень простой вид. Рассмотрим четырехмерную дивергенцию вектора j_μ :

Закон сохранения заряда утверждает, что утекание тока из единицы объема должно быть равно отрицательной скорости увеличения плотности заряда. Иными словами,

Подставляя это в (25.18), получаем очень простую форму закона сохранения заряда:

Благодаря тому что v_μj_μ— инвариант, равенство его нулю в одной системе отсчета означает равенство нулю и во всех других. Таким образом, если заряд сохраняется в одной системе, он будет сохраняться и во всех других системах координат, движущихся относительно нее с постоянной скоростью.
 
В качестве последнего примера рассмотрим скалярное произведение оператора градиента v_μ на себя. В трехмерном пространстве такое произведение дает лапласиан

Что получится для четырех измерений? Вычислить это очень просто. Следуя нашему правилу скалярного произведения, находим

Этот оператор, представляющий аналог трехмерного лапласиана, называется даламбертианом и обозначается специальным символом

По построению он является скалярным оператором, т. е., если подействовать им, скажем, на четырехвекторное поле, возникает новое четырехвекторное поле. [Иногда даламбертиан определяется с противоположным по отношению к (25.20) знаком, так что при чтении литературы будьте внимательны!]
 
Итак, для большинства величин, перечисленных нами в табл. 25.1, мы нашли их четырехмерные эквиваленты. (У нас еще нет эквивалента векторного произведения, но его нахождение мы оставим до следующей главы.) А теперь соберем в одно место все важнейшие результаты и определения и составим еще одну таблицу (табл. 25.2); она поможет вам лучше запомнить, что во что переходит.

СМОТРИТЕ ТАКЖЕ: