Главная >> Фейнмановские лекции по физике >> Том 6 >> Глава 24. Волноводы

Граничная частота

Уравнение (24.16) для k_z на самом деле имеет два корня — один с плюсом, другой с минусом. Ответ следует писать так:

Смысл этих двух знаков просто в том, что волны в волноводе могут бежать и с отрицательной фазовой скоростью (в направлении —z), и с положительной. Волны, естественно, должны иметь возможность бежать в любую сторону. И раз одновременно могут существовать оба типа волн, то решение в виде стоячих волн тоже возможно.
 
Наше уравнение для к_z сообщает нам также, что высшие частоты приводят к большим значениям k_z, т. е. к более коротким волнам, пока в пределе больших ω величина k не станет равной ω/с— тому значению, которое бывает, когда волна бежит в пустоте. Свет, который мы «видим» сквозь трубу, все еще бежит со скоростью с. Но посмотрите зато, какая странная вещь получается, когда частота убывает. Сперва волны становятся все длиннее и длиннее. Но если частота ω станет чересчур малой, то под корнем в  (24.20)   внезапно   появится   отрицательное число.  Это произойдет, когда ω перевалит через πс/а или когда λ_останет больше 2а. Иначе говоря, когда частота становится меньше некоторой критической частоты (ω_с=πс/а, волновое число k_z (а также λ_g ) становится мнимым и никакого решения у нас не остается. Или остается? Кто, собственно, сказал, что k_z должно быть действительным? Что случится, если оно станет мнимым? Уравнения-то поля по-прежнему ведь будут удовлетворяться. Может быть, и мнимые k_z тоже представляют какую-то волну?
 
Предположим, что ω действительно меньше ω_c; тогда можно написать

Если теперь вернуться к нашей формуле (24.12) для Е_y , то надо будет написать

Это выражение приводит к полю Е, которое во времени колеблется как e^¡wt, a пo z меняется как e^±k′z. Оно плавно убывает или возрастает с z, как всякая действительная экспонента. В нашем выводе мы не думали о том, откуда взялись волны, где их источник, но, конечно, где-то в волноводе он должен быть. И знак, который стоит при k′, должен быть таков, чтобы поле убывало при удалении от источника волн.

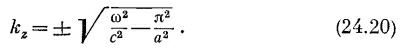
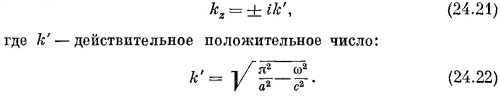
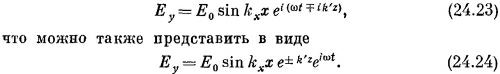
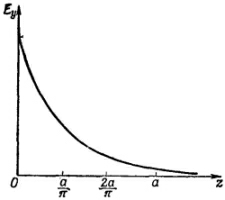Итак, при частотах ниже ω_с=πс/а волны вдоль трубы не распространяются; осциллирующее поле проникает в трубу лишь на расстояние порядка 1/k′. По этой причине частоту ω_c называют «граничной частотой» волновода. Глядя на (24.22), мы видим, что для частот чуть пониже ω_c число k′ мало, и поля могут проникать в трубу довольно далеко. Но если ω намного меньше ω_c, коэффициент k′ в экспоненте равняется π/а, и поле отмирает чрезвычайно быстро (фиг. 24.7). Поле убывает в е раз на расстоянии а/π, т. е. на трети ширины волновода. Поля проникают в волновод на очень малое расстояние от источника.
 
Мы хотим еще раз подчеркнуть эту характерную черту нашего анализа прохождения волн по трубе — появление мнимого волнового числа k_z. Когда, решая уравнение в физике, мы получаем мнимое число, то это обычно ничего физического не означает. Для волн, однако, мнимое волновое число действительно нечто означает. Волновое уравнение по-прежнему удовлетворяется; оно только означает, что решение приводит к экспоненциально убывающему полю вместо распространяющихся волн. Итак, если в любой задаче на волны k при какой-то частоте становится мнимым, это означает, что форма волны меняется — синусоида переходит в экспоненту.

СМОТРИТЕ ТАКЖЕ: