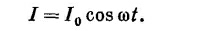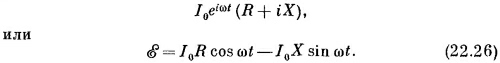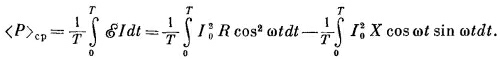| Обучение и материалы |
|---|
| Физический справочник |
| Формулы по физике |
| Шпаргалки по физике |
| Энциклопедия |
| Репетиторы по физике |
| Работа для физиков |
| Быстрый устный счет |
| Виртуальные лабораторные |
| Опыты по физике |
| ЕГЭ онлайн |
| Онлайн тестирование |
| Ученые физики |
| Необъяснимые явления |
| Ваша реклама на сайте |
| Разное |
| Контакты |
| Спецкурс |
|---|
| Фейнмановские лекции |
|
В мире больших скоростей |
Введение в теорию относительности |
|
Лекции по биофизике |
| Лекции по ядерной физике |
| Ускорение времени... |
| Лазеры |
| Нанотехнологии |
| Книги |
| полезное |
|---|
| Смешные анекдоты о физике
Готовые шпоры по физике Физика в жизни Ученые и деньги Нобелевские лауреаты Фото Видео Карта сайта |
| На заметку |
|---|
| Если вам понравился сайт, предлагаем разместить нашу кнопку |
| Дополнительно |
|---|
|
Компьютерные программы по физике 
Физика и юмор 
Онлайн тестирование по физике 
|
Энергия
Мы видели, что для создания в индуктивности тока / надо из внешней цепи доставить энергию U=1/2 LI2. Когда ток спадает до нуля, эта энергия уводится обратно во внешнюю цепь.
Чтобы найти, с какой средней скоростью подводится энергия, нужно усреднить произведение EI. Но теперь следует быть осторожным. Оперируя с такими произведениями, надо иметь дело только с действительными величинами E(t) и I(t). (Действительные части комплексных функций изображают настоящие физические величины только тогда, когда уравнения линейны; сейчас же речь идет о произведении, а это, несомненно, вещь нелинейная.)
Входящая в уравнение (22.25) э.д.с.— это действительная часть от
Два слагаемых в (22.26) представляют падение напряжений на R и X (см. фиг. 22.17). Мы видим, что падение напряжения на сопротивлении находится в фазе с током, тогда как падение напряжения на чисто реактивной части находится с током в противофазе.
Первый интеграл равен 1/2 I02R, а второй равен нулю. Стало быть, средняя потеря энергии в импедансе z=R+iX зависит лишь от действительной части z и равна I02R/2. Это согласуется с нашим прежним выводом о потерях энергии в сопротивлении. В реактивной части потерь энергии не бывает. СМОТРИТЕ ТАКЖЕ:Социальные комментарии Cackle |
При использовании материалов сайта ссылка на www.all-fizika.com обязательна.


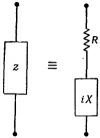 где R и X — числа действительные. С точки зрения эквивалентных схем можно сказать, что всякий импеданс эквивалентен сопротивлению, последовательно соединенному с чисто мнимым импедансом, называемым реактансом (фиг. 22.17).
где R и X — числа действительные. С точки зрения эквивалентных схем можно сказать, что всякий импеданс эквивалентен сопротивлению, последовательно соединенному с чисто мнимым импедансом, называемым реактансом (фиг. 22.17).