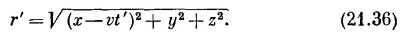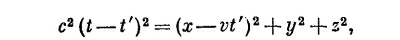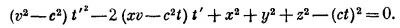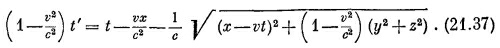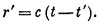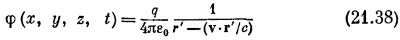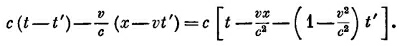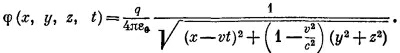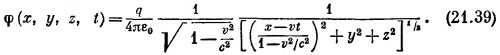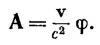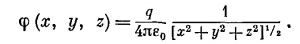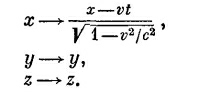| Обучение и материалы |
|---|
| Физический справочник |
| Формулы по физике |
| Шпаргалки по физике |
| Энциклопедия |
| Репетиторы по физике |
| Работа для физиков |
| Быстрый устный счет |
| Виртуальные лабораторные |
| Опыты по физике |
| ЕГЭ онлайн |
| Онлайн тестирование |
| Ученые физики |
| Необъяснимые явления |
| Ваша реклама на сайте |
| Разное |
| Контакты |
| Спецкурс |
|---|
| Фейнмановские лекции |
|
В мире больших скоростей |
Введение в теорию относительности |
|
Лекции по биофизике |
| Лекции по ядерной физике |
| Ускорение времени... |
| Лазеры |
| Нанотехнологии |
| Книги |
| полезное |
|---|
| Смешные анекдоты о физике
Готовые шпоры по физике Физика в жизни Ученые и деньги Нобелевские лауреаты Фото Видео Карта сайта |
| На заметку |
|---|
| Если вам понравился сайт, предлагаем разместить нашу кнопку |
| Дополнительно |
|---|
|
Компьютерные программы по физике 
Физика и юмор 
Онлайн тестирование по физике 
|
Потенциалы заряда, движущегося с постоянной скоростью. Формула Лоренца
где r′—расстояние от заряда до точки Р в этот запаздывающий момент. В это более раннее время t′ заряд был в x = vt′ так что
Чтобы найти r′ или t′, это уравнение надо сопоставить с (21.35). Исключим сперва r′, решив (21.35) относительно r′ и подставив в (21.36). Возвысив затем обе части в квадрат, получим
т. е. квадратное уравнение относительно t′. Раскрыв скобки и расположив члены по степеням t′, получим
Отсюда найдем
Чтобы получить r′, надо это t′ подставить в
Теперь мы уже можем найти φ из выражения (21.33), имеющего вид
(ввиду того, что v постоянно).
Подставляя (1—v2/c2)t′ из (21.37), получаем
Это уравнение становится более понятным, если переписать его в виде
Векторный потенциал А — это такое же выражение, но с добавочным множителем v/c2:
В выражении (21.39) со всей ясностью предстает перед вами начало преобразований Лоренца. Если бы заряд находился в начале координат в своей собственной системе покоя, то его потенциал имел бы вид
А мы смотрим на него из движущейся системы координат, и нам кажется, что координаты следует преобразовать с помощью Формул
Это обычное преобразование Лоренца. Лоренц вывел его тем же самым способом, каким пользовались и мы. СМОТРИТЕ ТАКЖЕ:Социальные комментарии Cackle |
При использовании материалов сайта ссылка на www.all-fizika.com обязательна.

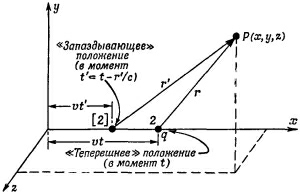 Применим теперь потенциалы Льенара — Вихерта к случаю заряда, движущегося по прямой с постоянной скоростью, и вычислим поле этого заряда. Позже мы повторим этот вывод, используя уже принцип относительности. Мы знаем величину потенциалов в той системе, в которой заряд покоится. Когда заряд движется, то все получается простым релятивистским преобразованием от одной системы к другой. Но теория относительности ведет свое начало от теории электричества и магнетизма. Формулы преобразований Лоренца [см. гл. 15 (вып. 2)] — это открытия, сделанные Лоренцем при исследовании уравнений электричества и магнетизма. И для того чтобы вы понимали, откуда все пошло, я хочу показать вам, что уравнения Максвелла действительно приводят к преобразованиям Лоренца. Я начну с вычисления потенциала равномерно движущегося заряда прямо из электродинамики, из уравнений Максвелла. Мы уже показали, что уравнения Максвелла приводят к потенциалу, полученному в предыдущем параграфе. Стало быть, пользуясь этими потенциалами, мы используем тем самым теорию Максвелла.
Применим теперь потенциалы Льенара — Вихерта к случаю заряда, движущегося по прямой с постоянной скоростью, и вычислим поле этого заряда. Позже мы повторим этот вывод, используя уже принцип относительности. Мы знаем величину потенциалов в той системе, в которой заряд покоится. Когда заряд движется, то все получается простым релятивистским преобразованием от одной системы к другой. Но теория относительности ведет свое начало от теории электричества и магнетизма. Формулы преобразований Лоренца [см. гл. 15 (вып. 2)] — это открытия, сделанные Лоренцем при исследовании уравнений электричества и магнетизма. И для того чтобы вы понимали, откуда все пошло, я хочу показать вам, что уравнения Максвелла действительно приводят к преобразованиям Лоренца. Я начну с вычисления потенциала равномерно движущегося заряда прямо из электродинамики, из уравнений Максвелла. Мы уже показали, что уравнения Максвелла приводят к потенциалу, полученному в предыдущем параграфе. Стало быть, пользуясь этими потенциалами, мы используем тем самым теорию Максвелла.