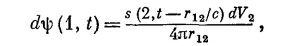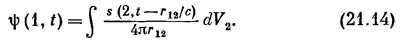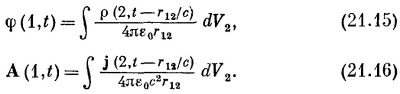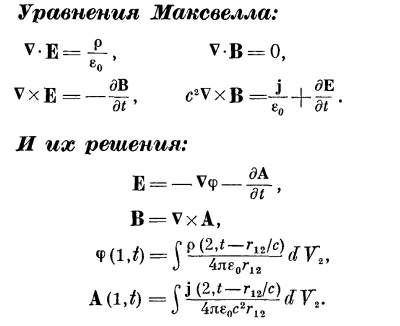| Обучение и материалы |
|---|
| Физический справочник |
| Формулы по физике |
| Шпаргалки по физике |
| Энциклопедия |
| Репетиторы по физике |
| Работа для физиков |
| Быстрый устный счет |
| Виртуальные лабораторные |
| Опыты по физике |
| ЕГЭ онлайн |
| Онлайн тестирование |
| Ученые физики |
| Необъяснимые явления |
| Ваша реклама на сайте |
| Разное |
| Контакты |
| Спецкурс |
|---|
| Фейнмановские лекции |
|
В мире больших скоростей |
Введение в теорию относительности |
|
Лекции по биофизике |
| Лекции по ядерной физике |
| Ускорение времени... |
| Лазеры |
| Нанотехнологии |
| Книги |
| полезное |
|---|
| Смешные анекдоты о физике
Готовые шпоры по физике Физика в жизни Ученые и деньги Нобелевские лауреаты Фото Видео Карта сайта |
| На заметку |
|---|
| Если вам понравился сайт, предлагаем разместить нашу кнопку |
| Дополнительно |
|---|
|
Компьютерные программы по физике 
Физика и юмор 
Онлайн тестирование по физике 
|
Общее решение уравнений Максвелла
Мы нашли решение уравнения (21.7) для «точечного» источника. Теперь встает новый вопрос: Каков вид решения для рассредоточенного источника? Ну, это решить легко; всякий источник s(x, у, z, t) можно считать состоящим из суммы многих «точечных» источников, расположенных поодиночке в каждом элементе объема dV и имеющих силу s(x, у, z, t)dV. Поскольку (21.7) линейно, суммарное поле представляет собой суперпозицию полей от всех таких элементов источника.
где r12 — расстояние от (2) до (1). Сложение вкладов от всех частей источника означает, конечно, интегрирование по всей области, где s≠0, так что мы имеем
Иначе говоря, поле в точке (1) в момент времени t представляет собой сумму всех сферических волн, испускаемых в момент t—r12 /c всеми элементами источника, расположенного в точке (2). Выражение (21.14) является решением нашего волнового уравнения для любой системы источников.
Поля Е и В получатся дифференцированием потенциалов [используются выражения (21.2) и (21.3)]. Кстати, можно проверить явно, что φ и А, полученные из (21.15) и (21.16), действительно удовлетворяют равенству (21.6).
СМОТРИТЕ ТАКЖЕ:Социальные комментарии Cackle |
© All-Физика, 2009-2026
При использовании материалов сайта ссылка на www.all-fizika.com обязательна.
При использовании материалов сайта ссылка на www.all-fizika.com обязательна.