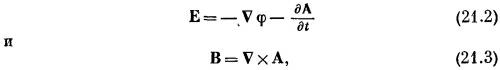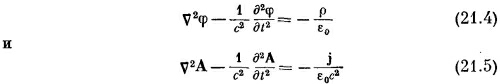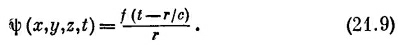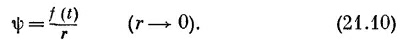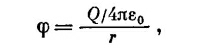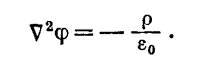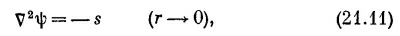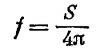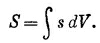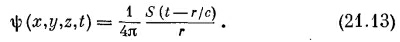Главная >> Фейнмановские лекции по физике >> Том 6 >> Глава 21. Решения уравнений Максвелла с токами и зарядами

Сферические волны от точечного источника

В гл. 18 мы установили, что уравнения  Максвелла можно решать подстановкой

где φ и А обязаны удовлетворять уравнениям

и, кроме того,  условию

Найдем теперь решение уравнений (21.4) и (21.5). Для этого надо уметь решать уравнение

где величина s (которая называется источником) известна. Ясно, что для уравнения (21.4) s соответствует ρ/ε₀, a ψ — это φ, а для уравнения (21.5) s соответствует j_x/ε₀c², если ψ — это А_х, и т. д. Но нас интересует чисто математическая задача решения (21.7) безотносительно к тому, каков физический смысл ψ и s.
 
Там, где ρ и j равны нулю (это место называется «пустотой»), там потенциалы φ и А и поля Е и В удовлетворяют трехмерному волновому уравнению без источников; математическая форма этого уравнения такова:

В гл. 20 мы видели, что решения этого уравнения могут представлять волны разных сортов: плоские волны, бегущие в x-направлении ψ=f(t—x/c); плоские волны, бегущие вдоль у или вдоль z или в любом другом направлении; сферические волны вида

(Решения можно записать иначе — например в виде цилиндрических  волн, разбегающихся от оси.)
 
Мы тогда заметили, что физически формула (21.9) относится не совсем к пустоте: в начале координат должны быть какие-то заряды, иначе расходящаяся волна не получилась бы. Иными словами, формула (21.9) есть решение уравнения (21.8) всюду, кроме непосредственной окрестности точки r=0, где (21.9) представляет собой решение полного уравнения (21.7), в правой части которого стоят источники. Давайте теперь посмотрим, что это за уравнение, т. е. какого рода источник s в уравнении (21.7) должен вызвать волну типа (21.9).
 
Предположим, что имеется сферическая волна (21.9) и поглядим, во что она превращается при очень малых r. Тогда запаздыванием  —r/с в f(t—r/с) можно пренебречь, и поскольку функция f плавная, ψ превращается в

Итак, ψ в точности похоже на кулоново поле заряда, расположенного в начале координат. Мы знаем, что для небольшого сгустка заряда, ограниченного очень малой областью близ начала координат и имеющего плотность ρ,

где Q= ∫ρdV. Такой потенциал φ удовлетворяет уравнению

Следуя тем же расчетам, мы должны были бы сказать, что φ из выражения (21.10) удовлетворяет уравнению

где s связано с f формулой

при

Единственная разница в том, что в общем случае s, а, стало быть, и S может оказаться функцией времени.
 
Далее очень важно то, что если ψ удовлетворяет (21.11) при малых r, то оно удовлетворяет также и (21.7). По мере приближения к началу координат зависимость ψ от r типа 1/r приводит к тому, что пространственные производные становятся очень большими. А производные по времени остаются теми же. [Это просто производные f(t) по времени.] Так что, когда r стремится к нулю, множителем ∂²ψ/∂t² в уравнении (21.7) по сравнению с v²ψ можно пренебречь, и (21.7) становится эквивалентным уравнению  (21.11).
 
Подытоживая, можно сказать, что если функция источника s(t) из уравнения (21.7) сосредоточена в начале координат и ее общая величина равна

то решение уравнения (21.7) имеет вид

Влияние слагаемого с ∂²ψ/∂t² в (21.7) сказывается лишь на появлении запаздывания (t—r/с) в потенциале кулонова типа.

СМОТРИТЕ ТАКЖЕ: