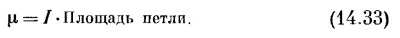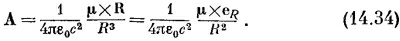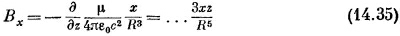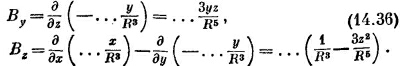| Обучение и материалы |
|---|
| Физический справочник |
| Формулы по физике |
| Шпаргалки по физике |
| Энциклопедия |
| Репетиторы по физике |
| Работа для физиков |
| Быстрый устный счет |
| Виртуальные лабораторные |
| Опыты по физике |
| ЕГЭ онлайн |
| Онлайн тестирование |
| Ученые физики |
| Необъяснимые явления |
| Ваша реклама на сайте |
| Разное |
| Контакты |
| Спецкурс |
|---|
| Фейнмановские лекции |
|
В мире больших скоростей |
Введение в теорию относительности |
|
Лекции по биофизике |
| Лекции по ядерной физике |
| Ускорение времени... |
| Лазеры |
| Нанотехнологии |
| Книги |
| полезное |
|---|
| Смешные анекдоты о физике
Готовые шпоры по физике Физика в жизни Ученые и деньги Нобелевские лауреаты Фото Видео Карта сайта |
| На заметку |
|---|
| Если вам понравился сайт, предлагаем разместить нашу кнопку |
| Дополнительно |
|---|
|
Компьютерные программы по физике 
Физика и юмор 
Онлайн тестирование по физике 
|
Поле маленькой петли. Магнитный диполь
Воспользуемся методом векторного потенциала, чтобы найти магнитное поле маленькой петли с током. Как обычно, под словом «маленькая» мы просто подразумеваем, что нас интересуют поля только на больших расстояниях по сравнению с размером петли. Как мы увидим, любая петелька представляет собой «магнитный диполь». Это значит, что она создает магнитное поле, подобное электрическому полю от электрического диполя.
где р — диполышй момент распределения зарядов. В данном случае дипольный момент равен полному заряду на одной палочке, умноженному на расстояние между ними:
Дипольный момент смотрит в отрицательном направлении y, поэтому косинус угла между R и р равен —ylR (где у — координата Р). Итак, мы имеем
Заменяя λ на I/с2, сразу же получаем Аx
С помощью тех же рассуждений:
Векторный потенциал маленькой плоской петельки любой формы (круг, треугольник и т. п.) также дается уравнениями (14.30) и (14.31), если заменить lab на
Мы предоставляем вам право это доказать.
Нам еще нужно найти В. Пользуясь (14.33) и (14.34), а также (14.4), получаем
(под многоточием мы подразумеваем μ/4πε0c2),
Компоненты поля В ведут себя точно так же, как компоненты поля Е для диполя, ориентированного вдоль оси z [см. уравнения (6.14) и (6.15), а также фиг. 6.5, стр. 115]. Вот почему мы называем петлю магнитным диполем. Слово «диполь» в применении к магнитному полю немного запутывает, потому что нет отдельных магнитных «полюсов», соответствующих электрическим зарядам. Магнитное «динольное поле» создается не двумя «зарядами», а элементарной петлей с током. СМОТРИТЕ ТАКЖЕ:Социальные комментарии Cackle |
© All-Физика, 2009-2025
При использовании материалов сайта ссылка на www.all-fizika.com обязательна.
При использовании материалов сайта ссылка на www.all-fizika.com обязательна.

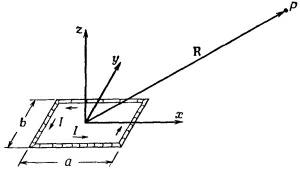 Возьмем сначала прямоугольную петлю и выберем оси координат, как показано на фиг. 14.6. Токов в направлении z нет, поэтому Аz равно нулю. Есть токи в направлении х по обеим сторонам прямоугольника, длина которых а.
Возьмем сначала прямоугольную петлю и выберем оси координат, как показано на фиг. 14.6. Токов в направлении z нет, поэтому Аz равно нулю. Есть токи в направлении х по обеим сторонам прямоугольника, длина которых а.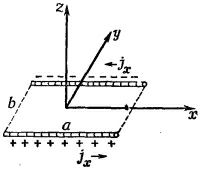 В каждой стороне плотность тока и ток однородны. Поэтому решение для Ах в точности подобно электростатическому потенциалу от двух заряженных палочек (фиг. 14-7). Поскольку палочки имеют противоположные заряды, их электрический потенциал на больших расстояниях есть как раз дипольный потенциал (см. гл. 6, § 5). В точке Р на фиг. 14.6 потенциал равен
В каждой стороне плотность тока и ток однородны. Поэтому решение для Ах в точности подобно электростатическому потенциалу от двух заряженных палочек (фиг. 14-7). Поскольку палочки имеют противоположные заряды, их электрический потенциал на больших расстояниях есть как раз дипольный потенциал (см. гл. 6, § 5). В точке Р на фиг. 14.6 потенциал равен

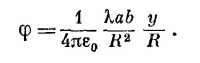


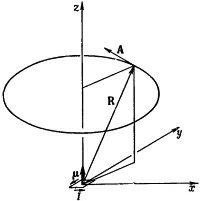 Снова Ау пропорционально х, а Ах пропорционально —у, так что векторный потенциал (на больших расстояниях) идет по кругу вокруг оси z, циркулируя таким же образом, как ток / в петле (фиг. 14.8).
Снова Ау пропорционально х, а Ах пропорционально —у, так что векторный потенциал (на больших расстояниях) идет по кругу вокруг оси z, циркулируя таким же образом, как ток / в петле (фиг. 14.8).