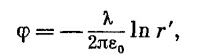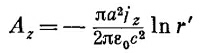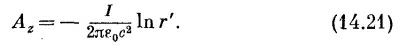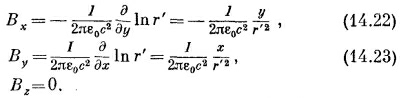| Обучение и материалы |
|---|
| Физический справочник |
| Формулы по физике |
| Шпаргалки по физике |
| Энциклопедия |
| Репетиторы по физике |
| Работа для физиков |
| Быстрый устный счет |
| Виртуальные лабораторные |
| Опыты по физике |
| ЕГЭ онлайн |
| Онлайн тестирование |
| Ученые физики |
| Необъяснимые явления |
| Ваша реклама на сайте |
| Разное |
| Контакты |
| Спецкурс |
|---|
| Фейнмановские лекции |
|
В мире больших скоростей |
Введение в теорию относительности |
|
Лекции по биофизике |
| Лекции по ядерной физике |
| Ускорение времени... |
| Лазеры |
| Нанотехнологии |
| Книги |
| полезное |
|---|
| Смешные анекдоты о физике
Готовые шпоры по физике Физика в жизни Ученые и деньги Нобелевские лауреаты Фото Видео Карта сайта |
| На заметку |
|---|
| Если вам понравился сайт, предлагаем разместить нашу кнопку |
| Дополнительно |
|---|
|
Компьютерные программы по физике 
Физика и юмор 
Онлайн тестирование по физике 
|
Прямой провод
внутри провода и нулю вне его.
где r′=√х2+у2, а λ — заряд на единицу длины πа2ρ. Следовательно, Аz должно быть равно
для точек вне длинного провода с равномерно распределенным током. Поскольку πа2jz =I, то можно также написать
Теперь можно найти В, пользуясь (14.4). Из шести производных от нуля отличны только две. Получаем
Мы получаем тот же результат, что и раньше: В обходит провод по окружности и по величине равен
СМОТРИТЕ ТАКЖЕ:Социальные комментарии Cackle |
© All-Физика, 2009-2026
При использовании материалов сайта ссылка на www.all-fizika.com обязательна.
При использовании материалов сайта ссылка на www.all-fizika.com обязательна.

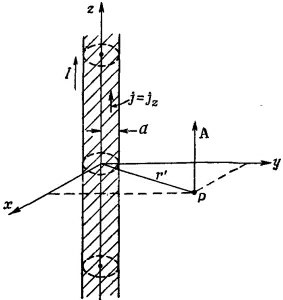 В качестве первого примера снова вычислим поле прямого провода, которое мы находили в предыдущем параграфе, пользуясь уравнением (14.2) и соображениями симметрии. Возьмем длинный прямой провод радиуса а, по которому течет постоянный ток /. В отличие от заряда в проводнике в случае электростатики постоянный ток в проводе распределен равномерно по поперечному сечению провода. При таком выборе координат, как показано на фиг. 14.3, вектор плотности тока j имеет только z-компоненту. По величине она равна
В качестве первого примера снова вычислим поле прямого провода, которое мы находили в предыдущем параграфе, пользуясь уравнением (14.2) и соображениями симметрии. Возьмем длинный прямой провод радиуса а, по которому течет постоянный ток /. В отличие от заряда в проводнике в случае электростатики постоянный ток в проводе распределен равномерно по поперечному сечению провода. При таком выборе координат, как показано на фиг. 14.3, вектор плотности тока j имеет только z-компоненту. По величине она равна