| Обучение и материалы |
|---|
| Физический справочник |
| Формулы по физике |
| Шпаргалки по физике |
| Энциклопедия |
| Репетиторы по физике |
| Работа для физиков |
| Быстрый устный счет |
| Виртуальные лабораторные |
| Опыты по физике |
| ЕГЭ онлайн |
| Онлайн тестирование |
| Ученые физики |
| Необъяснимые явления |
| Ваша реклама на сайте |
| Разное |
| Контакты |
| Спецкурс |
|---|
| Фейнмановские лекции |
|
В мире больших скоростей |
Введение в теорию относительности |
|
Лекции по биофизике |
| Лекции по ядерной физике |
| Ускорение времени... |
| Лазеры |
| Нанотехнологии |
| Книги |
| полезное |
|---|
| Смешные анекдоты о физике
Готовые шпоры по физике Физика в жизни Ученые и деньги Нобелевские лауреаты Фото Видео Карта сайта |
| На заметку |
|---|
| Если вам понравился сайт, предлагаем разместить нашу кнопку |
| Дополнительно |
|---|
|
Компьютерные программы по физике 
Физика и юмор 
Онлайн тестирование по физике 
|
Векторный потенциал заданных токов
Раз В определяется токами, значит, и А тоже. Мы хотим теперь выразить А через токи. Начнем с нашего основного уравнения (14.2):
откуда, конечно, следует
Это уравнение для магнитостатики; оно похоже на уравнение
для электростатики.
Поскольку мы выбрали v·А = 0 (и теперь вы видите, почему), уравнение (14.12) приобретает вид
Это векторное уравнение, конечно, распадается на три уравнения
и каждое из этих уравнений математически идентично уравнению
Все, что мы узнали о нахождении потенциала для известного ρ, можно использовать для нахождения каждой компоненты А, когда известно j!
Тогда мы немедленно получаем общее решение для Ах:
(Вы можете при желании проверить прямым дифференцированием компонент, что этот интеграл удовлетворяет v·А=0, поскольку v·j=0, а последнее, как мы видели, должно выполняться для постоянных токов.) СМОТРИТЕ ТАКЖЕ:Социальные комментарии Cackle |
© All-Физика, 2009-2026
При использовании материалов сайта ссылка на www.all-fizika.com обязательна.
При использовании материалов сайта ссылка на www.all-fizika.com обязательна.

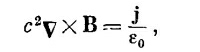
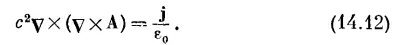

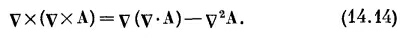

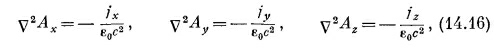

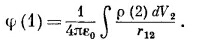
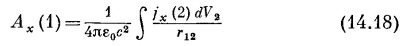
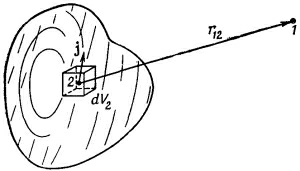 и аналогично для Аy и Az. (Фиг. 14.2 напоминает вам о принятых нами обозначениях для г12 и dV2.) Мы можем объединить все три решения в векторной форме:
и аналогично для Аy и Az. (Фиг. 14.2 напоминает вам о принятых нами обозначениях для г12 и dV2.) Мы можем объединить все три решения в векторной форме: