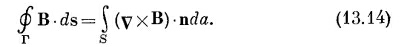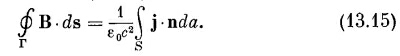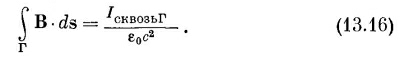| Обучение и материалы |
|---|
| Физический справочник |
| Формулы по физике |
| Шпаргалки по физике |
| Энциклопедия |
| Репетиторы по физике |
| Работа для физиков |
| Быстрый устный счет |
| Виртуальные лабораторные |
| Опыты по физике |
| ЕГЭ онлайн |
| Онлайн тестирование |
| Ученые физики |
| Необъяснимые явления |
| Ваша реклама на сайте |
| Разное |
| Контакты |
| Спецкурс |
|---|
| Фейнмановские лекции |
|
В мире больших скоростей |
Введение в теорию относительности |
|
Лекции по биофизике |
| Лекции по ядерной физике |
| Ускорение времени... |
| Лазеры |
| Нанотехнологии |
| Книги |
| полезное |
|---|
| Смешные анекдоты о физике
Готовые шпоры по физике Физика в жизни Ученые и деньги Нобелевские лауреаты Фото Видео Карта сайта |
| На заметку |
|---|
| Если вам понравился сайт, предлагаем разместить нашу кнопку |
| Дополнительно |
|---|
|
Компьютерные программы по физике 
Физика и юмор 
Онлайн тестирование по физике 
|
Магнитное поле постоянного тока. Закон Ампера
Мы видели, что на проволоку в магнитном поле, создаваемом, скажем, магнитом, действует сила. Из закона о том, что действие равно противодействию, можно ожидать, что, когда по проволоке протекает ток, возникает сила, действующая на источник магнитного поля, т. е. на магнит. Такие силы действительно существуют; в этом можно убедиться по отклонению стрелки компаса вблизи проволоки с током. Далее, мы знаем, что магниты испытывают действие сил со стороны других магнитов, а отсюда вытекает, что когда по проволоке течет ток, то он создает собственное магнитное поле. Значит, движущиеся заряды создают магнитное поле. Попытаемся понять законы, которым подчиняются такие магнитные поля. Вопрос ставится так: дан ток, какое магнитное поле он создаст? Ответ на этот вопрос был получен экспериментально тремя опытами и подтвержден блестящим теоретическим доказательством Ампера. Мы не будем останавливаться на этой интересной истории, а просто скажем, что большое число экспериментов наглядно показало справедливость уравнений Максвелла. Их мы и возьмем в качестве отправной точки. Опуская в уравнениях члены с производными по времени, мы получаем уравнения магнитостатики
Эти уравнения справедливы только при условии, что все плотности электрических зарядов и все токи постоянны, так что электрические и магнитные поля не меняются со временем — все поля «статические».
Найдя rot B из уравнения (13.13), имеем
Интеграл от j по S, согласно (13.5), есть полный ток / через поверхность S. Поскольку для постоянных токов ток через S не зависит от формы S, если она ограничена кривой Г, то обычно говорят о «токе через замкнутую петлю Г». Мы имеем, таким образом, общий закон: циркуляция В по любой замкнутой кривой равна току / сквозь петлю, деленному на ε0с2:
Этот закон, называемый законом Ампера, играет такую же роль в магнитостатике, как закон Гаусса в электростатике. Один лишь закон Ампера не определяет В через токи; мы должны, вообще говоря, использовать также v·В=0. Но, как мы увидим в следующем параграфе, он может быть использован для нахождения поля в тех особых случаях, которые обладают некоторой простой симметрией. СМОТРИТЕ ТАКЖЕ:Социальные комментарии Cackle |
При использовании материалов сайта ссылка на www.all-fizika.com обязательна.

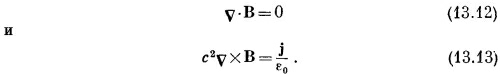
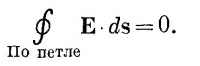
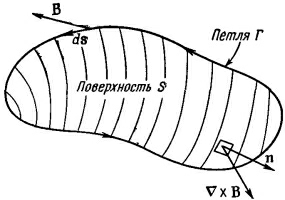 Мы получили этот результат с помощью теоремы Стокса, согласно которой интеграл по любому замкнутому пути от любого векторного поля равен поверхностному интегралу от нормальной компоненты ротора этого вектора (интеграл берется по любой поверхности, натянутой на данный контур). Применяя эту же теорему к вектору магнитного поля и используя обозначения, показанные на фиг. 13.6, получаем
Мы получили этот результат с помощью теоремы Стокса, согласно которой интеграл по любому замкнутому пути от любого векторного поля равен поверхностному интегралу от нормальной компоненты ротора этого вектора (интеграл берется по любой поверхности, натянутой на данный контур). Применяя эту же теорему к вектору магнитного поля и используя обозначения, показанные на фиг. 13.6, получаем