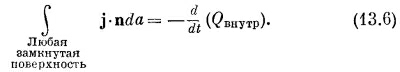| Обучение и материалы |
|---|
| Физический справочник |
| Формулы по физике |
| Шпаргалки по физике |
| Энциклопедия |
| Репетиторы по физике |
| Работа для физиков |
| Быстрый устный счет |
| Виртуальные лабораторные |
| Опыты по физике |
| ЕГЭ онлайн |
| Онлайн тестирование |
| Ученые физики |
| Необъяснимые явления |
| Ваша реклама на сайте |
| Разное |
| Контакты |
| Спецкурс |
|---|
| Фейнмановские лекции |
|
В мире больших скоростей |
Введение в теорию относительности |
|
Лекции по биофизике |
| Лекции по ядерной физике |
| Ускорение времени... |
| Лазеры |
| Нанотехнологии |
| Книги |
| полезное |
|---|
| Смешные анекдоты о физике
Готовые шпоры по физике Физика в жизни Ученые и деньги Нобелевские лауреаты Фото Видео Карта сайта |
| На заметку |
|---|
| Если вам понравился сайт, предлагаем разместить нашу кнопку |
| Дополнительно |
|---|
|
Компьютерные программы по физике 
Физика и юмор 
Онлайн тестирование по физике 
|
Электрический ток. Сохранение заряда
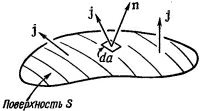
Подумаем теперь о том, почему магнитные силы действуют на провода, по которым течет электрический ток. Для этого определим, что понимается под плотностью тока. Электрический ток состоит из движущихся электронов или других зарядов, которые образуют результирующее течение, или поток. Мы можем представить поток зарядов вектором, определяющим количество зарядов, которое проходит в единицу времени через единичную площадку, перпендикулярную потоку (точь-в-точь как мы это делали, определяя поток тепла). Назовем эту величину плотностью тока и обозначим ее вектором j. Он направлен вдоль движения зарядов. Если взять маленькую площадку Δа в данном месте материала, то количество зарядов, текущее через площадку в единицу времени, равно
Заряд, проходящий в единицу времени, тогда равен ρv·nΔa, откуда получаем
Если распределение зарядов состоит из отдельных зарядов, скажем электронов с зарядом q, движущихся со средней скоростью v, то плотность тока равна
Ток I из замкнутой поверхности S представляет собой скорость, с которой заряды покидают объем V, окруженный поверхностью S. Один из основных законов физики говорит, что электрический заряд неуничтожаем; он никогда не теряется и не создается. Электрические заряды могут перемещаться с места на место, но никогда не возникают из ничего. Мы говорим, что заряд сохраняется. Если из замкнутой поверхности возникает результирующий ток, то количество заряда внутри должно соответственно уменьшаться (фиг. 13.4). Поэтому мы можем записать закон сохранения заряда в таком виде:
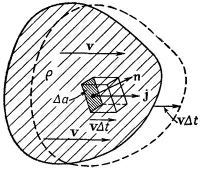
Заряд внутри можно записать как объемный интеграл от плотности заряда
Применяя (13.6) к малому объему ΔV, можно учесть, что интеграл слева есть v·j ΔV. Заряд внутри равен ρΔV, поэтому сохранение заряда можно еще записать и так:
(опять теорема Гаусса из математики!). СМОТРИТЕ ТАКЖЕ:Социальные комментарии Cackle |
© All-Физика, 2009-2026
При использовании материалов сайта ссылка на www.all-fizika.com обязательна.
При использовании материалов сайта ссылка на www.all-fizika.com обязательна.


 где n — единичный вектор нормали к Δа.
где n — единичный вектор нормали к Δа.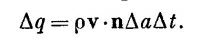


 где N — число зарядов в единице объема.
где N — число зарядов в единице объема.