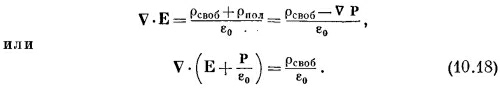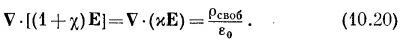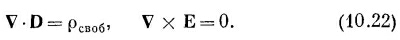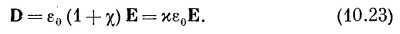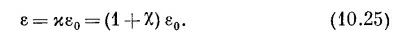Главная >> Фейнмановские лекции по физике >> Том 5 >> Глава 10. Диэлектрики

Уравнения электростатики для диэлектриков

Давайте теперь свяжем полученные нами результаты с тем, что мы уже узнали в электростатике. Основное уравнение имеет вид

где ρ — плотность всех электрических зарядов. Поскольку уследить за поляризационными зарядами непросто, удобно разбить ρ на две части. Обозначим снова через ρ_пол заряды, появляющиеся за счет неоднородной поляризации, а остальную часть назовем ρ_своб. Обычно ρ_сво6 означает заряд, сообщаемый проводникам или распределенный известным образом в пространстве. В этом случае уравнение (10.17)  приобретает вид

Уравнение для ротора от Е, конечно, не меняется:

Подставляя Р из уравнения (10.8), получаем более простое уравнение:

Это и есть уравнения электростатики в присутствии диэлектриков. Они, конечно, не дают ничего нового, но имеют вид, более удобный для расчетов в тех случаях, когда ρ_своб известно, а поляризация Р пропорциональна E.
 
Заметьте, что мы не вытащили «константу» диэлектрической проницаемости х за знак дивергенции. Это потому, что она может не быть всюду одинаковой. Если она повсюду одинакова, то ее можно выделить в качестве множителя и уравнения станут в точности обычными уравнениями электростатики, где только ρ_своб нужно поделить на х. В написанной нами форме уравнения годятся в общем случае, когда в разных местах поля расположены разные диэлектрики. В таких случаях решить уравнения иногда бывает очень трудно.
 
Здесь следует отметить один момент, имеющий историческое значение. На заре рождения электричества атомный механизм поляризации не был еще известен и о существовании ρ_пол не знали. Заряд ρ_своб считался равным всей плотности зарядов. Чтобы придать уравнениям Максвелла простой вид, вводили новый вектор D как линейную комбинацию Е и Р:

В результате уравнения (10.18) и (10.19) записывались в очень простом виде:

Можно ли их решить? Только когда задано третье уравнение, связывающее D и Е. Если справедливо уравнение (10.8), то эта связь есть

Последнее уравнение обычно записывается так:

где ε — еще одна постоянная, описывающая диэлектрические свойства материалов. Она также называется «проницаемостью». (Теперь вы понимаете, почему в наших уравнениях  появилось ε₀, это «проницаемость пустого пространства».)
 
Очевидно,

Сейчас мы рассматриваем эти вещи уже с другой точки зрения, а именно что в вакууме всегда имеются самые простые уравнения, и если в каждом случае учесть все заряды, какова бы ни была причина их возникновения, то они всегда справедливы. Выделяя часть зарядов либо из соображений удобства, либо потому, что мы не хотим вникать в детали процесса, мы всегда можем при желании написать уравнения в любой удобной для нас форме.
 
Сделаем еще одно замечание. Уравнение D = εЕ представляет собой попытку описать свойства вещества. Но вещество исключительно сложно по своей природе, и подобное уравнение на самом деле неправильно. Так, если Е становится очень большим, D перестает быть пропорциональным Е. В некоторых веществах пропорциональность нарушается уже при достаточно слабых полях. Кроме того, «константа» пропорциональности может зависеть от того, насколько быстро Е меняется со временем. Следовательно, уравнение такого типа есть нечто вроде приближенного уравнения типа закона Гука. Оно не может быть глубоким, фундаментальным уравнением. С другой стороны, наши основные уравнения для Е (10.17) и (10.19) выражают наиболее полное и глубокое понимание электростатики.

СМОТРИТЕ ТАКЖЕ: