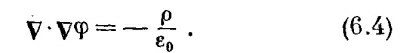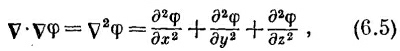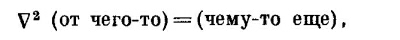Главная >> Фейнмановские лекции по физике >> Том 5 >> Глава 6. Электрическое поле в разных физических условиях

Уравнения электростатического потенциала

В  этой  главе  мы  расскажем  о  поведении электрического поля в тех или иных обстоятельствах. Вы познакомитесь с тем, как ведет себя электрическое поле, и с некоторыми математическими методами, используемыми для определения поля.                                                    
 
Отметим для начала, что математически вся задача состоит в  решении двух уравнений — максвелловских уравнений электростатики:           

Фактически оба эти уравнения  можно объединить в одно. Из второго уравнения сразу же следует, что поле может считаться градиентом некоего скаляра  (см. гл. 3, § 7):   

Электрическое  поле каждого частного вида можно, если нужно,  полностью описать с помощью потенциала  поля φ.  Дифференциальное   уравнение,  которому должно  удовлетворять φ, получится, если (6.3) подставить в (6.1):

Расходимость градиента φ — это то же, что v², действующее на φ:

так что уравнение (6.4) мы запишем в виде

Оператор v² называется лапласианом, а уравнение (6.6) — уравнением Пуассона. Весь предмет электростатики с математической точки зрения заключается просто в изучении решений одного-единственного уравнения (6.6). Как только из (6.6) вы найдете φ, поле Е немедленно получается из (6.3).
 
Обратимся сперва к особому классу задач, в которых ρ задано как функция х, у, z. Такая задача почти тривиальна, потому что решать уравнение. (6.6) в общем случае мы уже умеем. Мы ведь показали, что если ρ в каждой точке известно, то потенциал в точке (1) равен

где ρ(2) — плотность заряда, dV₂ — элемент объема в точке (2), а r₁₂ — расстояние между точками (1) и (2). Решение дифференциального уравнения (6.6) свелось к интегрированию по пространству. Решение (6.7) нужно отметить особо, потому что в физике часто встречаются ситуации, приводящие к уравнениям, которые выглядят так:

и (6.7) является прототипом решения любой такой задачи.
 
Проблема расчета электростатического поля, таким образом, решается совершенно честно, если только положения всех зарядов известны. Давайте посмотрим на нескольких примерах, как действует эта формула.

СМОТРИТЕ ТАКЖЕ: