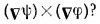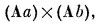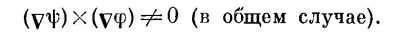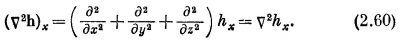Главная >> Фейнмановские лекции по физике >> Том 5 >> Глава 2. Дифференциальное исчисление векторных полей

Подвохи

Мы применили наши знания обычной векторной алгебры к алгебре оператора v. Здесь нужно быть осторожным, иначе легко напутать. Нужно упомянуть о двух подвохах (впрочем, в нашем курсе они не встретятся). Что можете вы сказать о следующем выражении, куда входят две скалярные функции -ψ и φ (фи):

Вы можете подумать, что это нуль, потому что оно похоже на

а это всегда равно нулю (векторное произведение двух одинаковых векторов АхА всегда нуль). Но в нашем примере два оператора v отнюдь не одинаковы! Первый действует на одну функцию, ψ, а второй — на другую, φ. И хотя мы изображаем их одним и тем же значком v, они все же должны рассматриваться как разные операторы. Направление vψ зависит от функции ψ, а направление vφ — от функции φ, так что они не обязаны быть параллельными:

К счастью, к таким выражениям мы прибегать не будем. (Но сказанное нами не меняет того факта, что vφ Х vψ=0 в любом скалярном поле: здесь обе v действуют на одну и ту же функцию.) Подвох номер два (он тоже в нашем курсе не встретится): правила, которые мы здесь наметили, выглядят просто и красиво только в прямоугольных координатах. Например, если мы хотим написать x-компоненту выражения v²h, то сразу пишем

Но это выражение не годится, если мы ищем радиальную компоненту v²h. Она не равна v²h_r. Дело в том, что в алгебре векторов все их направления полностью определены. А когда мы имеем дело с векторными полями, то их направления в разных местах различны. Когда мы пробуем описать векторное поле, например, в полярных координатах, то «радиальное» направление меняется от точки к точке. И начав дифференцировать компоненты, вы запросто можете попасть в беду. Даже в постоянном векторном поде радиальная компонента от точки к точке меняется.
 
Обычно безопаснее и проще всего держаться прямоугольных координат. Но стоит упомянуть и одно исключение: поскольку лапласиан v² есть скаляр, то можно писать его в любой системе координат (скажем, в полярных координатах). Но так как это дифференциальный оператор, то применять его надо только к векторам с фиксированным направлением компонент, т. е. к заданным в прямоугольных координатах. Итак, расписывая наши векторные дифференциальные уравнения покомпонентно, мы будем предварительно выражать все наши векторные поля через их х-, у-, z-компоненты.

СМОТРИТЕ ТАКЖЕ: