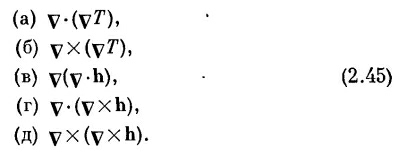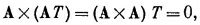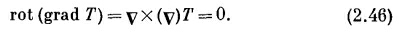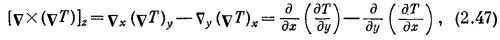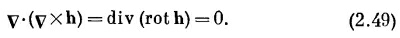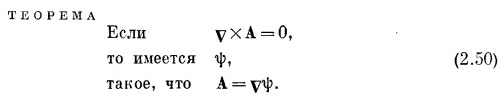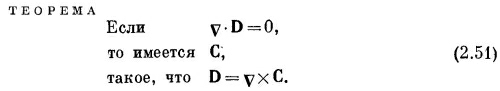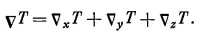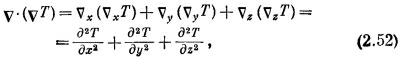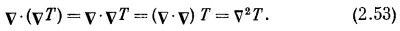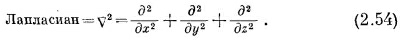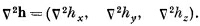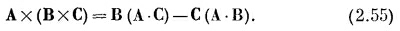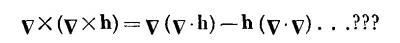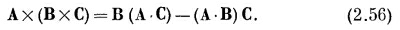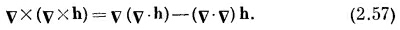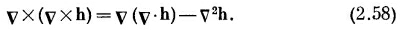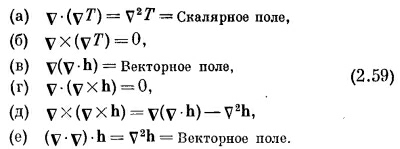Главная >> Фейнмановские лекции по физике >> Том 5 >> Глава 2. Дифференциальное исчисление векторных полей

Вторые производные векторных полей

Пока мы имели дело только с первыми производными. А почему не со вторыми? Из вторых производных можно составить несколько комбинаций:

Вы можете убедиться, что никаких иных комбинаций быть не может.
 
Посмотрим сперва на вторую комбинацию (б). Она имеет ту же форму, что и

потому что А Х А всегда нуль. Значит,

Можно понять, как это получается, если расписать одну из компонент:

что равно нулю [по уравнению (2.8)]. Это же верно и для других компонент. Стало быть, vХ(vТ)=0 для любого распределения температур, да и для всякой скалярной функции.
 
Возьмем второй пример. Посмотрим, нельзя ли получить нуль другим путем. Скалярное произведение вектора на векторное произведение, содержащее этот вектор, равно нулю

потому что Ах В перпендикулярно к А и не имеет тем самым составляющих вдоль А. Сходная комбинация стоит в списке  (2.45) под номером (г):

В справедливости этого равенства опять-таки легко убедиться, проделав выкладки на компонентах.
 
Теперь сформулируем без доказательства две теоремы. Они очень интересны и весьма полезны для физиков.
 
В физических задачах часто оказывается, что ротор какой-то величины (скажем, векторного поля А) равен нулю. Мы видели в уравнении (2.46), что ротор градиента равен нулю. (Это легко запоминается по свойствам векторов.) Далее, может оказаться, что А будет градиентом какой-то величины, потому что тогда ротор А с необходимостью обратится в нуль. Имеется интересная теорема, утверждающая, что если ротор А есть нуль, то тогда А непременно окажется чьим-то градиентом; существует некоторое скалярное поле ψ (пси), такое, что A=grad ψ. Иными словами, справедлива

Сходная теорема формулируется и для случая, когда дивергенция А есть нуль. Из уравнения (2.49) видно, что дивергенция ротора любой величины равна всегда нулю. Если вам случайно встретилось векторное поле D, для которого div D — нуль, то вы имеете право заключить, что D это ротор некоторого векторного поля С.

Перебирая всевозможные сочетания двух операторов v, мы обнаружили, что два из них всегда дают нуль. Займемся теперь теми, которые не равны нулю. Возьмем комбинацию v·(vТ), первую в нашем списке. В общем случае это не нуль. Выпишем компоненты

Далее,

что может, вообще говоря, быть любым числом. Это скалярное поле.
 
Вы видите, что скобок можно не ставить, а вместо этого писать, не рискуя ошибиться:

Можно рассматривать v² как новый оператор. Это скалярный оператор. Так как он в физике встречается часто, ему дали особое имя — лапласиан.

Раз оператор лапласиана — оператор скалярный, он может действовать и на вектор. Под этим мы подразумеваем, что он применяется к каждой компоненте вектора

Рассмотрим еще одну возможность: vX(vXh) [(д) в списке (2.45)]. Ротор от ротора можно написать иначе, если использовать векторное равенство (2.6)

Заменим в этой формуле А и В оператором v и положим C=h. Получится

Погодите-ка! Здесь что-то не так. Как и положено, первые два члена — векторы (операторы утолили свою жажду), но последний член совсем не такой. Он все еще оператор. Ошибка в том, что мы не были осторожны и не выдержали нужного порядка членов. Вернувшись обратно, вы увидите, что (2.55) можно с равным успехом записать в виде

Такой порядок членов выглядит уже лучше. Сделаем нашу подстановку в (2.56). Получится

С этой формулой уже все в порядке. Она действительно правильна, в чем вы можете убедиться, расписав компоненты. Последний член — это лапласиан, так что с равным успехом можно написать

Из нашего списка (2.45) двойных v мы разобрали все комбинации, кроме (в), v(v·h). В ней есть смысл, это — векторное поле, но больше сказать о ней нечего. Это просто векторное поле, которое может случайно возникнуть в каком-нибудь расчете.
 
Удобно будет все наши рассуждения свести теперь в таблицу:

Вы могли заметить, что мы не пытались изобрести новый векторный оператор vХv. Понимаете, почему?

СМОТРИТЕ ТАКЖЕ: