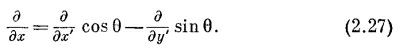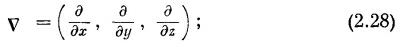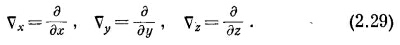| Обучение и материалы |
|---|
| Физический справочник |
| Формулы по физике |
| Шпаргалки по физике |
| Энциклопедия |
| Репетиторы по физике |
| Работа для физиков |
| Быстрый устный счет |
| Виртуальные лабораторные |
| Опыты по физике |
| ЕГЭ онлайн |
| Онлайн тестирование |
| Ученые физики |
| Необъяснимые явления |
| Ваша реклама на сайте |
| Разное |
| Контакты |
| Спецкурс |
|---|
| Фейнмановские лекции |
|
В мире больших скоростей |
Введение в теорию относительности |
|
Лекции по биофизике |
| Лекции по ядерной физике |
| Ускорение времени... |
| Лазеры |
| Нанотехнологии |
| Книги |
| полезное |
|---|
| Смешные анекдоты о физике
Готовые шпоры по физике Физика в жизни Ученые и деньги Нобелевские лауреаты Фото Видео Карта сайта |
| На заметку |
|---|
| Если вам понравился сайт, предлагаем разместить нашу кнопку |
| Дополнительно |
|---|
|
Компьютерные программы по физике 
Физика и юмор 
Онлайн тестирование по физике 
|
Оператор V
А сейчас мы проделаем крайне занятную и остроумную вещь — одну из тех, которые так украшают математику. Доказательство того, что grad T, или vТ, является вектором, не зависит от того, какое скалярное поле мы дифференцируем. Все доводы остались бы в силе, если бы Т было заменено любым скалярным полем. А поскольку уравнения преобразований одинаковы независимо от того, что дифференцируется, то можно Т убрать и уравнение (2.26) заменить операторным уравнением
Как выразился Джинс, мы оставляем операторы «жаждущими продифференцировать что угодно».
это означает, конечно,
Мы-абстрагировали градиент от T — в этом и есть остроумие.
а это не число, а все еще какой-то оператор. Однако в согласии с алгеброй векторов Тv по-прежнему можно называть вектором.
но нужно помнить, что операторная алгебра немного отличается от обычной векторной. Надо всегда выдерживать правильный порядок операторов, чтобы их операции имели смысл. Тогда у вас трудностей не возникнет, если вы припомните, что оператор v подчиняется тем же условиям, что и производные. То, что вы дифференцируете, должно быть поставлено справа от v. Порядок здесь существен. СМОТРИТЕ ТАКЖЕ:Социальные комментарии Cackle |
© All-Физика, 2009-2026
При использовании материалов сайта ссылка на www.all-fizika.com обязательна.
При использовании материалов сайта ссылка на www.all-fizika.com обязательна.