Главная >> Фейнмановские лекции по физике >> Том 4 >> Глава 50. Гармоники

Ряд Фурье

В предыдущей главе мы познакомились с другой точкой зрения на колеблющуюся систему. Мы видели, что в струне возникают различные собственные гармоники и что любое частное колебание, которое только возможно получить из начальных условий, можно рассматривать как составленную в надлежащей пропорции комбинацию нескольких одновременно осциллирующих собственных гармоник. Для струны мы нашли, что собственные гармоники имеют частоты ω₀, 2ω₀, Зω₀, ... . Поэтому наиболее общее движение струны складывается из синусоидальных колебаний основной частоты ω₀, затем второй гармоники 2ω₀, затем третьей гармоники Зω₀ и т. д. Основная гармоника повторяется через каждый период T₁=2π/ω₀, вторая гармоника — через каждый период T₂=2π/2ω₀; она повторяется также и через каждый период Т₁=2Т₂, т. е. после двух своих периодов. Точно таким же образом через период Т₁ повторяется и третья гармоника. В этом отрезке укладываются три ее периода. И снова мы понимаем, почему задетая струна через период Т₁ полностью повторяет форму своего движения. Так получается музыкальный звук.
 
До сих пор мы говорили о движении струны. Однако звук, который представляет собой движение воздуха, вызванное движением струны, тоже должен состоять из тех же гармоник, хотя здесь мы уже не можем говорить о собственных гармониках воздуха. К тому же относительная сила различных гармоник в воздухе может быть совсем другой, чем в струне, особенно если струна «связана» с воздухом посредством «звучащей доски». Разные гармоники по-разному связаны с воздухом.
 
Если для музыкального тона функция f(t) представляет давление воздуха в зависимости от времени (скажем, такая, как на фиг. 50.1,6), то можно ожидать, что f(t) записывается в виде суммы некоторого числа простых гармонических функций от времени (подобных cos ωt) для каждой из различных гармонических частот. Если период колебаний равен Т, то основная угловая частота будет ω=2π/T, а следующие гармоники будут 2ω, Зω и т. д.
 
Здесь появляется небольшое усложнение. Мы не вправе ожидать, что для каждой частоты начальные фазы обязательно будут равны друг другу. Поэтому нужно пользоваться функциями типа cos (ωt + φ)- Вместо этого, однако, проще использовать для каждой частоты как синус, так и косинус. Напомним, что

а поскольку φ — постоянная, то любые синусоидальные колебания с частотой со могут быть записаны в виде суммы членов, в один из которых входит sin ωt, а в другой — cos ωt.
 
Итак, мы приходим к заключению, что любая периодическая функция f(t) с периодом Т математически может быть записана в виде

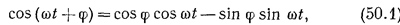
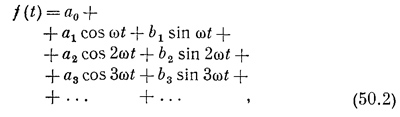
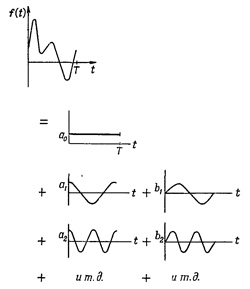где ω=2π/T, а а и b — числовые постоянные, указывающие, с каким весом каждая компонента колебания входит в общее колебание f(t). Для большей общности мы добавили в нашу формулу член с нулевой частотой а₀, хотя обычно для музыкальных тонов он равен нулю. Это просто сдвиг средней величины звукового давления (т. е. сдвиг «нулевого» уровня). С этим членом наша формула верна для любого случая. Уравнение (50.2) схематически показано на фиг. 50.2. Амплитуды гармонических функций а_n и b_n выбираются по специальному правилу. На рисунке они показаны только схематически без соблюдения масштаба. [Ряд (50.2) называется рядом Фурье для функций f(t).]

Мы сказали, что любую периодическую функцию можно написать в таком виде. Следует внести небольшую поправку и подчеркнуть, что в такой ряд можно разложить вообще любую звуковую волну или любую функцию, с которой мы сталкиваемся в физике. Математики, конечно, могут придумать такую функцию, что ее нельзя будет составить из простых гармонических (например, функцию, которая «заворачивает» назад, так что для некоторых величин t она имеет два значения!). Однако здесь нам не стоит беспокоиться о таких функциях.

СМОТРИТЕ ТАКЖЕ: