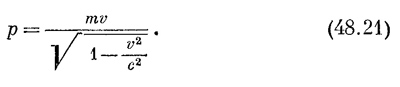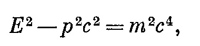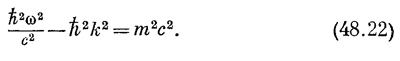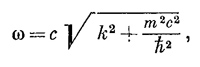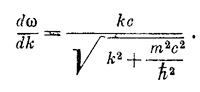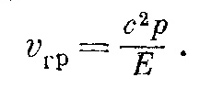| Обучение и материалы |
|---|
| Физический справочник |
| Формулы по физике |
| Шпаргалки по физике |
| Энциклопедия |
| Репетиторы по физике |
| Работа для физиков |
| Быстрый устный счет |
| Виртуальные лабораторные |
| Опыты по физике |
| ЕГЭ онлайн |
| Онлайн тестирование |
| Ученые физики |
| Необъяснимые явления |
| Ваша реклама на сайте |
| Разное |
| Контакты |
| Спецкурс |
|---|
| Фейнмановские лекции |
|
В мире больших скоростей |
Введение в теорию относительности |
|
Лекции по биофизике |
| Лекции по ядерной физике |
| Ускорение времени... |
| Лазеры |
| Нанотехнологии |
| Книги |
| полезное |
|---|
| Смешные анекдоты о физике
Готовые шпоры по физике Физика в жизни Ученые и деньги Нобелевские лауреаты Фото Видео Карта сайта |
| На заметку |
|---|
| Если вам понравился сайт, предлагаем разместить нашу кнопку |
| Дополнительно |
|---|
|
Компьютерные программы по физике 
Физика и юмор 
Онлайн тестирование по физике 
|
Амплитуда вероятности частиц
Рассмотрим еще один необычайно интересный пример фазовой скорости. Он относится к области квантовой механики. Известно, что амплитуда вероятности найти частицу в данном месте изменяется при некоторых обстоятельствах в пространстве и времени (давайте возьмем одно измерение) следующим образом:
Точно таким же образом импульс равен
Как следствие отсюда после исключения v получается
т. е. рμрμ =т2. Это величайший результат четырехмерья, о котором мы уже говорили много раз, устанавливающий связь между энергией и импульсом в классической теории. Теперь же, поскольку мы собираемся заменить Е и р на ω и k с помощью подстановки Е=hω и р=hк, он означает, что в квантовой механике должна существовать связь
Таким образом, возникло соотношение между частотой и волновым числом квантовомеханической амплитуды, описывающей частицу с массой т. Из этого уравнения можно получить
т. е. фазовая скорость ω/k снова больше скорости света!
Но входящий сюда квадратный корень есть попросту ω/с, так что эту формулу можно записать в виде dω/dk=с2k/ω. Далее, так как k/ω равно р/Е, то
Но, согласно (48.20) и (48.21), с2р/Е равно v — скорости частицы в классической механике. Таким образом видно, что, принимая во внимание основные квантовомеханические соотношения E=hω и p=hk, определяющие ω и k через классические величины Е и р и дающие только уравнение ω2—k2с2 = m2c4/h2, теперь можно понять также соотношения (48.20) и (48.21), связывающие Е и р со скоростью. Групповая скорость, разумеется, должна быть скоростью частиц, если эта интерпретация вообще имеет какой-либо смысл. Пусть в какой-то момент, как мы полагаем, частица находится в одном месте, а затем, скажем через 10 минут,— в другом. Тогда, согласно квантовой механике, расстояние, пройденное «колоколом», разделенное на интервал времени, должно равняться классической скорости частицы. СМОТРИТЕ ТАКЖЕ:Социальные комментарии Cackle |
При использовании материалов сайта ссылка на www.all-fizika.com обязательна.


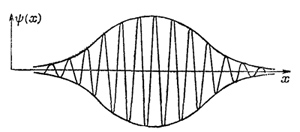 где ω — частота, связанная с классической энергией, E=hω, а k — волновое число, которое связано с импульсом соотношением р = hk. Мы говорим, что частица имеет определенный импульс р, если волновое число в точности равно k, т. е. если бежит идеальная волна повсюду с одинаковой амплитудой. Выражение (48.19) дает амплитуду вероятности, но если мы возьмем квадрат абсолютной величины, то получим относительную вероятность обнаружения частицы как функцию положения и времени. В данном случае она равна постоянной, что означает вероятность обнаружить частицу в любом месте. Рассмотрим теперь такой случай, когда известно, что обнаружить частицу в каком-то месте более вероятно, чем в других местах. Подобную картину мы описываем волной, которая имеет максимум в данном месте и сходит на нет по мере удаления в стороны (фиг. 48.6). (Это не то же самое, что изображено на фиг. 48.1, где волна имеет целый ряд максимумов, но сними вполне можно расправиться, сложив несколько волн с приблизительно одинаковыми значениями ω и k. Таким способом можно избавиться от всех максимумов, кроме одного.)
где ω — частота, связанная с классической энергией, E=hω, а k — волновое число, которое связано с импульсом соотношением р = hk. Мы говорим, что частица имеет определенный импульс р, если волновое число в точности равно k, т. е. если бежит идеальная волна повсюду с одинаковой амплитудой. Выражение (48.19) дает амплитуду вероятности, но если мы возьмем квадрат абсолютной величины, то получим относительную вероятность обнаружения частицы как функцию положения и времени. В данном случае она равна постоянной, что означает вероятность обнаружить частицу в любом месте. Рассмотрим теперь такой случай, когда известно, что обнаружить частицу в каком-то месте более вероятно, чем в других местах. Подобную картину мы описываем волной, которая имеет максимум в данном месте и сходит на нет по мере удаления в стороны (фиг. 48.6). (Это не то же самое, что изображено на фиг. 48.1, где волна имеет целый ряд максимумов, но сними вполне можно расправиться, сложив несколько волн с приблизительно одинаковыми значениями ω и k. Таким способом можно избавиться от всех максимумов, кроме одного.)