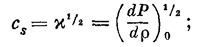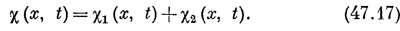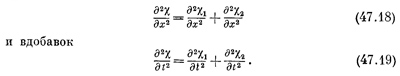Главная >> Фейнмановские лекции по физике >> Том 4 >> Глава 47. Звук. Волновое уравнение

Решения волнового уравнения

Посмотрим теперь, действительно ли волновое уравнение описывает основные свойства звуковых волн в среде. Прежде всего мы хотим вывести, что звуковое колебание, или возмущение, движется с постоянной скоростью. Кроме того, нам нужно доказать, что два различных колебания могут свободно проходить друг через друга, т. е. принцип суперпозиции. Мы хотим еще доказать, что звук может распространяться и вправо и влево. Все эти свойства должны содержаться в нашем одном уравнении.
 
Раньше мы отмечали, что любое возмущение, имеющее вид плоской волны и движущееся с постоянной скоростью, записывается в виде f(x—vt). Посмотрим теперь, является ли f(x—vt) решением волнового уравнения. Вычисляя дχ/дх, получаем производную функции dχ/dx=f`(x—vt). Дифференцируя еще раз, находим

Дифференцируя эту же функцию χ по t, получаем значение — v, умноженное на производную, или dχ/dt =—vf`(x — vt); вторая производная по времени дает

Очевидно, что f(х — vt)   удовлетворяет волновому уравнению, если v равно c_s.
Таким образом, из законов механики мы получаем, что любое звуковое возмущение распространяется со скоростью c_s и, кроме того,

тем самым мы   связали  скорость  звуковых  волн со свойствами среды.

Легко увидеть, что звуковая волна может распространяться и в направлении отрицательных х, т. е. звуковое возмущение вида χ(х, t)=g(x+vt) также удовлетворяет волновому уравнению. Единственное отличие этой волны от той, которая распространялась слева направо, заключается в знаке v, но знак d²χ/dt² не зависит от выбора x+vt или х—vt, потому что в эту производную входит только v². Отсюда следует, что решение уравнения описывает волны, бегущие в любом направлении со скоростью c_s.


Особый интерес представляет вопрос о суперпозиции решений. Допустим, мы нашли одно решение, скажем χ₁. Это значит, что вторая производная χ₁. по х равна второй производной χ₁ по t, умноженной на 1/с²_s. И пусть есть второе решение χ₂ обладающее тем же свойством. Сложим эти два решения, тогда получается

Теперь мы хотим удостовериться, что χ(х, t) тоже представляет некую волну, т. е. χ тоже удовлетворяет волновому уравнению. Это очень просто доказать, так как

Отсюда следует, что d²χ/dx² = (1/c²_s)d²χldt², так что справедливость принципа суперпозиции проверена. Само существование принципа суперпозиции связано с тем, что волновое уравнение линейно по χ.


Теперь естественно было бы ожидать, что плоская световая волна, распространяющаяся вдоль оси х и поляризованная так, что электрическое поле направлено по оси у, тоже удовлетворяет волновому уравнению

где с — скорость света. Волновое уравнение для световой волны есть одно из следствий уравнений Максвелла. Уравнения электродинамики приводят к волновому уравнению для света точно так же, как уравнения механики приводят к волновому уравнению для звука.

СМОТРИТЕ ТАКЖЕ: