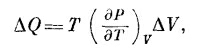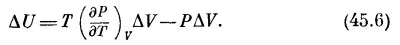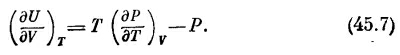| Обучение и материалы |
|---|
| Физический справочник |
| Формулы по физике |
| Шпаргалки по физике |
| Энциклопедия |
| Репетиторы по физике |
| Работа для физиков |
| Быстрый устный счет |
| Виртуальные лабораторные |
| Опыты по физике |
| ЕГЭ онлайн |
| Онлайн тестирование |
| Ученые физики |
| Необъяснимые явления |
| Ваша реклама на сайте |
| Разное |
| Контакты |
| Спецкурс |
|---|
| Фейнмановские лекции |
|
В мире больших скоростей |
Введение в теорию относительности |
|
Лекции по биофизике |
| Лекции по ядерной физике |
| Ускорение времени... |
| Лазеры |
| Нанотехнологии |
| Книги |
| полезное |
|---|
| Смешные анекдоты о физике
Готовые шпоры по физике Физика в жизни Ученые и деньги Нобелевские лауреаты Фото Видео Карта сайта |
| На заметку |
|---|
| Если вам понравился сайт, предлагаем разместить нашу кнопку |
| Дополнительно |
|---|
|
Компьютерные программы по физике 
Физика и юмор 
Онлайн тестирование по физике 
|
Внутренняя энергия
Когда приходится использовать термодинамику для дела, то оказывается, что она очень трудный и сложный предмет. В этой книге, однако, мы не будем залезать в самые дебри. Эта область особенно интересна для химиков и инженеров, и тем, кому захочется получше познакомиться с ней, следует обратиться к физической химии или инженерной термодинамике. Есть еще ряд хороших справочных книг, в которых эта тема обсуждается более подробно. Термодинамика сложна потому, что каждое явление она позволяет описывать многими способами. Если нам нужно описать поведение газа, то мы можем исходить из того, что его давление зависит от температуры и объема, а можно предположить, что объем зависит от давления и температуры. То же самое и с внутренней энергией U: можно сказать, что она определяется температурой и объемом, стоит только выбрать именно эти переменные, но можно говорить о зависимости от температуры и давления или от давления и объема и т. д. В предыдущей главе мы познакомились с другой функцией температуры и объема, называемой энтропией S. И теперь ничто не помешает нам построить другие функции этих переменных. Например, функция U—TS тоже зависит от температуры и объема. Таким образом, нам приходится иметь дело с большим количеством разных величин, зависящих от разнообразных комбинаций переменных. Чтобы упростить понимание этой главы, договоримся с самого начала выбрать в качестве независимых переменных температуру и объем. Химики используют для этого температуру и давление, потому что их легче измерять и контролировать в химических реакциях. Но мы используем повсюду в этой главе температуру и объем и изменим этому только в одном месте, чтобы посмотреть, как совершается переход к химическим переменным. Итак, сначала рассмотрим только одну систему независимых переменных — температуру и объем. Затем нас будут интересовать только две функции этих переменных: внутренняя энергия и давление. Все другие термодинамические функции можно получить с помощью этих двух, но не обязательно это делать именно сейчас. Даже после таких ограничений термодинамика останется еще трудным предметом, но все же уже не столь невозможным для понимания! Сначала немного займемся математикой. Если величина есть функция от двух переменных, то дифференцировать ее придется осторожнее, чем мы это делали раньше, имея дело с одной переменной. Что мы понимаем под производной давления по температуре? Изменение давления, сопровождающее изменение температуры, разумеется, зависит от того, что случилось с объемом, пока менялась температура. Прежде чем понятие производной по температуре обретет ясный смысл, надо сказать что-то определенное об изменении объема. Например, можно спросить, какова скорость изменения Р относительно Т при постоянном объеме. Тогда отношение изменений обеих этих величин, по существу, обычная производная, которой привыкли присваивать символ dP/dT. Мы обычно используем особый символ ∂Р/∂Т, он напоминает нам, что Р зависит, кроме Т, еще и от переменной V, и эта переменная не изменяется. Чтобы подчеркнуть тот факт, что V не изменяется, мы не только используем символ ∂, но еще пометим индексом остающуюся постоянной переменную (∂Р/∂Т)v. Конечно, поскольку имеются только две независимые переменные, то это обозначение излишне, но оно, быть может, поможет нам легче пройти сквозь термодинамические дебри частных производных. Предположим, что функция f(x, у) зависит от двух независимых переменных х и у. Под символом (∂f /∂х)у мы понимаем самую обычную производную, получаемую общепринятым способом, если у постоянна:
Аналогично определяется и
Например, если f(x, у)=х2+ух, то (∂f /∂х)y =2х +у, a (∂f /∂y)x=x. Мы можем распространить это на старшие производные: ∂2f /∂y2 или ∂2f /∂y∂x. Последний случай означает, что сначала f продифференцировано по х, считая у постоянным, а затем результат продифференцирован по у, но теперь постоянным стало х. Порядок дифференцирования не имеет значения: ∂2f /∂x∂y=∂2f /∂y∂x. Нам придется подсчитывать изменение Δf, происходящее с f (x,y), если х переходит в х +Δх, а у переходит в у +Δу. Будем предполагать, что Δх и Δу бесконечно малы:
Последнее уравнение и есть основное соотношение, связывающее приращение Δf с Δх и Δу. Посмотрим, как используется это соотношение; для этого вычислим изменение внутренней энергии U (T, V), если температура Т переходит в T+ ΔT, а объем V переходит в V +ΔV. Используем формулу (45.1) и запишем
В предыдущей главе мы нашли другое выражение для изменения внутренней энергии ΔU; тогда к подводимому газу прибавлялось тепло ΔQ:
Сравнив (45.2) и (45.3), можно было бы подумать, что P=(∂U /∂V)T, но это не так. Чтобы получить верный результат, сначала предположим, что газ получает тепло ΔQ, причем объем его не изменяется, так что ΔV=0. Если ΔV=0, то уравнение (45.3) говорит нам, что ΔU=ΔQ, а уравнение (45.2) утверждает, что ΔU=(∂U /∂T)v ΔT, поэтому (∂U /∂T)v=ΔQ /ΔT. Отношение ΔQ /ΔT—количество тепла, которое нужно подвести к телу,чтобы изменить его температуру на один градус, удерживая объем постоянным,— называется удельной теплоемкостью при постоянном объеме и обозначается символом Сv. Таким образом, мы показали, что
Теперь снова подведем к газу тепло ΔQ, но на этот раз договоримся, что температура газа останется постоянной, а объему мы позволим измениться на ΔV. В этом случае анализ сложнее, но мы можем вычислить ΔU, используя аргументы Карно, для чего нам придется снова призвать на помощь цикл Карно из предыдущей главы.
Соберем все наши выводы вместе.
Выражение (45.5) содержит в себе суть результатов, следующих из аргументов Карно. Всю термодинамику можно вывести из (45.5) и первого закона, содержащегося в уравнении (45.3). Выражение (45.5)— это, в сущности, второй закон, хотя впервые Карно сформулировал его несколько иначе, поскольку не пользовался нашим определением температуры. А теперь можно приступить к вычислению (∂U /∂V)T. Насколько изменится внутренняя энергия U, если объем изменится на ΔV? Во-первых, внутренняя энергия U меняется за счет подводимого тепла и, во-вторых, за счет совершаемой работы. Подводимое тепло, согласно (45.5), равно
а совершаемая над веществом работа равна —PΔV. Поэтому изменение ΔU складывается из двух кусков
Поделив обе стороны на ΔV, мы найдем скорость изменения U относительно V при постоянной Т
В нашей термодинамике, где есть только две переменные, T и V, и только две функции, Р и U, уравнения (45.3) и (45.7) — это основные уравнения, из которых можно вывести все последующие результаты. СМОТРИТЕ ТАКЖЕ:Социальные комментарии Cackle |
При использовании материалов сайта ссылка на www.all-fizika.com обязательна.

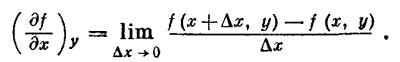
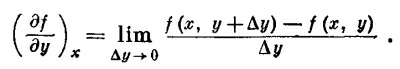
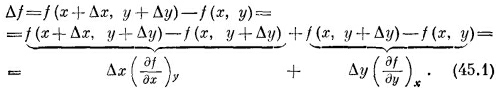
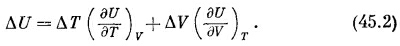


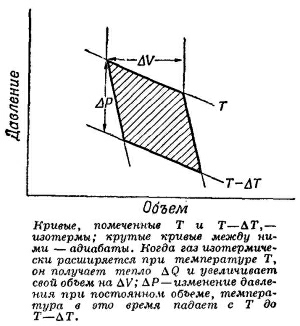 Диаграмма давление — объем для цикла Карно изображена на фиг. 45.1. Мы уже показали, что полная работа, совершаемая газом при обратимом цикле, равна ΔQ(ΔT/T), где ΔQ — тепло, подводимое к газу при температуре Т во время изотермического расширения от V до V+ΔV, а Т—ΔT — это конечная температура, которой достигает газ при адиабатическом расширении на втором этапе цикла. Сейчас мы покажем, что эта работа равна, кроме того, заштрихованной площади на фиг. 45.1. Работа газа во всех случаях жизни равна ∫ PdV; она положительна, если газ расширяется, и отрицательна, когда он сжимается. Если вычертить зависимость Р от V, то изменения Р и V изобразятся кривой, в каждой точке которой определенному значению Р соответствует определенное значение V. Работа, произведенная газом, пока его объем изменяется от одного значения до другого (интеграл ∫ PdV),— это площадь под кривой, соединяющей начальное и конечное значения V. Применим эту идею к циклу Карно и убедимся, что если обойти цикл, помня о знаке совершенной газом работы, то чистая работа газа будет равна заштрихованной на фиг. 45.1 площади.
Диаграмма давление — объем для цикла Карно изображена на фиг. 45.1. Мы уже показали, что полная работа, совершаемая газом при обратимом цикле, равна ΔQ(ΔT/T), где ΔQ — тепло, подводимое к газу при температуре Т во время изотермического расширения от V до V+ΔV, а Т—ΔT — это конечная температура, которой достигает газ при адиабатическом расширении на втором этапе цикла. Сейчас мы покажем, что эта работа равна, кроме того, заштрихованной площади на фиг. 45.1. Работа газа во всех случаях жизни равна ∫ PdV; она положительна, если газ расширяется, и отрицательна, когда он сжимается. Если вычертить зависимость Р от V, то изменения Р и V изобразятся кривой, в каждой точке которой определенному значению Р соответствует определенное значение V. Работа, произведенная газом, пока его объем изменяется от одного значения до другого (интеграл ∫ PdV),— это площадь под кривой, соединяющей начальное и конечное значения V. Применим эту идею к циклу Карно и убедимся, что если обойти цикл, помня о знаке совершенной газом работы, то чистая работа газа будет равна заштрихованной на фиг. 45.1 площади.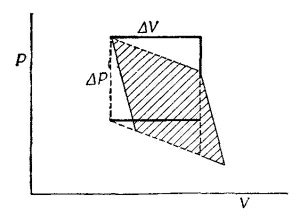 А теперь вычислим эту площадь чисто геометрически. Цикл, который был использован для получения фиг. 45.1, отличается от цикла, описанного в предыдущей главе тем, что теперь ΔQ и ΔT бесконечно малы. Наши адиабаты и изотермы очень близки друг к другу, поэтому фигура, описанная жирными линиями на фиг. 45.1, приближается к параллелограмму, когда приращения ΔQ и ΔT стремятся к нулю. Площадь этого параллелограмма в точности равна ΔVΔP (где ΔV — изменение объема, когда к газу подводится энергия ΔQ при постоянной температуре, а ΔР — изменение давления при изменении температуры на ΔT и постоянном объеме). Легко показать, что заштрихованная площадь на фиг. 45.1 равна площади, ограниченной пунктиром на фиг. 45.2. А эту фигуру легко превратить в прямоугольник со сторонами ΔP и ΔV, для чего нужно лишь вырезать из нее треугольники и сложить их немного иначе.
А теперь вычислим эту площадь чисто геометрически. Цикл, который был использован для получения фиг. 45.1, отличается от цикла, описанного в предыдущей главе тем, что теперь ΔQ и ΔT бесконечно малы. Наши адиабаты и изотермы очень близки друг к другу, поэтому фигура, описанная жирными линиями на фиг. 45.1, приближается к параллелограмму, когда приращения ΔQ и ΔT стремятся к нулю. Площадь этого параллелограмма в точности равна ΔVΔP (где ΔV — изменение объема, когда к газу подводится энергия ΔQ при постоянной температуре, а ΔР — изменение давления при изменении температуры на ΔT и постоянном объеме). Легко показать, что заштрихованная площадь на фиг. 45.1 равна площади, ограниченной пунктиром на фиг. 45.2. А эту фигуру легко превратить в прямоугольник со сторонами ΔP и ΔV, для чего нужно лишь вырезать из нее треугольники и сложить их немного иначе.