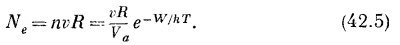| Обучение и материалы |
|---|
| Физический справочник |
| Формулы по физике |
| Шпаргалки по физике |
| Энциклопедия |
| Репетиторы по физике |
| Работа для физиков |
| Быстрый устный счет |
| Виртуальные лабораторные |
| Опыты по физике |
| ЕГЭ онлайн |
| Онлайн тестирование |
| Ученые физики |
| Необъяснимые явления |
| Ваша реклама на сайте |
| Разное |
| Контакты |
| Спецкурс |
|---|
| Фейнмановские лекции |
|
В мире больших скоростей |
Введение в теорию относительности |
|
Лекции по биофизике |
| Лекции по ядерной физике |
| Ускорение времени... |
| Лазеры |
| Нанотехнологии |
| Книги |
| полезное |
|---|
| Смешные анекдоты о физике
Готовые шпоры по физике Физика в жизни Ученые и деньги Нобелевские лауреаты Фото Видео Карта сайта |
| На заметку |
|---|
| Если вам понравился сайт, предлагаем разместить нашу кнопку |
| Дополнительно |
|---|
|
Компьютерные программы по физике 
Физика и юмор 
Онлайн тестирование по физике 
|
Испарение
Эта глава посвящена дальнейшим применениям кинетической теории. В предыдущей главе мы подчеркнули один из выводов этой теории, что средняя кинетическая энергия каждой степени свободы молекулы или любого другого объекта равна 1/2 kТ. Сейчас центральным пунктом нашего изложения будет утверждение о том, что отнесенная к единице объема вероятность обнаружить частицу в том или ином месте пропорциональна ехр(—п.э./kT). (Это утверждение мы используем в ряде задач.) Явления, которые мы собираемся изучить, довольно сложны: испарение жидкости, вылет электронов с поверхности металла или химическая реакция, в которой участвует много атомов. В таких случаях кинетическая теория не дает простых и точных предписаний, ситуация слишком сложна для этого. Поэтому выводы этой главы, за исключением особо оговоренных, весьма неточны. Мы только подчеркнем, что, исходя из кинетической теории, можно более или менее хорошо понять эти явления. Но гораздо более точное представление о них дают термодинамические аргументы или некоторые измерения отдельных критических величин. Однако полезно знать, хотя бы очень приблизительно, почему то, что происходит, происходит именно так. Тогда, натолкнувшись на явление, которое содержит в себе нечто, чего мы еще не видели, или то, что проанализировать мы еще не собрались, мы, может быть, сможем более или менее точно сказать, что произошло. Такой анализ будет в высшей степени неточным, но в общих чертах верным —верным по сути, но чуть-чуть упрощенным, скажем, в некоторых тонких деталях. Разберем первый пример — испарение жидкости. Предположим, что большой ящик при заданной температуре заполнен жидкостью и паром поровну. Будем считать, что средние расстояния между молекулами пара довольно велики, а вот в жидкости они упакованы плотно. Задача состоит в том, чтобы определить число молекул, находящихся в газовой фазе, по сравнению с числом молекул, находящихся в жидкости. Какова плотность пара при заданной температуре и как она зависит от температуры? Пусть n —число молекул пара в единице объема. Это число, естественно, меняется с температурой. С притоком тепла испарение увеличивается. Добавим еще одну величину 1/Va, равную числу атомов в единице объема, содержащихся в жидкости; мы предполагаем, что в жидкости каждой молекуле отведен вполне определенный объем, поэтому чем больше в жидкости молекул, тем больший объем они занимают. Если Vа — объем, отведенный одной молекуле, то число молекул в единичном объеме равно единичному объему, деленному на объем, занимаемый молекулой. Далее, предположим, что между молекулами действуют силы притяжения, удерживающие их внутри жидкости. Иначе нельзя понять, почему происходит конденсация. Итак, предположим, что имеется сила притяжения и существует энергия связи молекулы в жидкости, которая теряется при переходе молекул в пар. Это наводит на мысль, что для перевода какой-нибудь молекулы из жидкости в пар, нужно совершить работу W. Существует определенная разность W между энергией молекулы в жидкости и ее энергией в паре, потому что для переноса молекул в пар мы должны оторвать ее от всех молекул, к которым она притягивается. Теперь обратимся к общему принципу, по которому отношение числа атомов в единице объема в разных областях равно n2/n1= ехр[—(Е2—Е1)/kТ]. Значит, n —число молекул в единичном объеме пара, деленное на 1/Va (число молекул в единичном объеме жидкости), равно
Таково общее правило. Это очень похоже на равновесную атмосферу в поле тяжести, когда низшие слои газа плотнее верхних, потому что для подъема молекулы на высоту h нужна энергия mgh. В жидкости молекулы размещены плотнее, чем в газе, так как их заставляет потесниться энергия «подъема» W, и отношение плотностей равно ехр(—W/kT). Это как раз то, что мы хотели вывести — плотность пара изменяется как е в некоторой степени. Показателем служит взятая со знаком минус похожая на энергию величина, деленная на kТ. Множители перед экспонентой не особенно интересны, потому что в большинстве случаев плотность пара гораздо меньше плотности жидкости. При этих обстоятельствах, когда мы далеки от критической точки, где плотности почти одинаковы, соотношение плотностей, при котором n много меньше 1/Va, обеспечивается тем, что W много больше kТ. Поэтому формулы типа (42.1) интересны только тогда, когда W действительно гораздо больше kТ; в этом случае е возводится в громадную отрицательную степень и если немного изменить Т, то изменится слегка и громадная степень, а это изменение повлечет за собой такие изменения экспоненты, которые будут гораздо важнее возможных изменений предэкспоненциальных множителей. Но отчего бы изменяться таким множителям, как 1/Va? Да оттого, что наше описание приблизительно. Ведь в действительности каждая молекула не имеет определенного объема; при изменении температуры объем Va не остается постоянным — жидкости сжимаются и расширяются. Есть еще и другие мелочи вроде этой, так что действительная ситуация гораздо сложнее. Почти всюду стоят медленно изменяющиеся с температурой множители. В действительности само W медленно изменяется с температурой, потому что при разных температурах молекулам отведены разные объемы, и притяжение должно быть разным, и т. д. Итак, можно прийти к выводу, что поскольку у нас получилась формула, в которой все неизвестным образом изменяется с температурой, то на самом деле формулы никакой и нет. Но если мы знаем, что показатель у экспоненты W/kT заведомо велик, то можно убедиться, что наибольшие изменения кривой плотности пара как функции температуры обусловлены экспоненциальным множителем. Поэтому если мы будем считать W постоянной величиной, а коэффициент 1/Va — почти постоянной, то это будет хорошим приближением вдоль небольшого интервала нашей кривой. Иначе говоря, основные изменения определяются видом функции exp(–W/kT). Выходит, что в природе есть много, очень много процессов, для которых характерно взятие энергии взаймы; основным свойством таких процессов является экспоненциальная температурная зависимость: е возводится в отношение взятой с отрицательным знаком энергии kТ, Это полезный факт, но только в тех случаях, когда энергия велика по сравнению с kТ, поскольку главная часть изменений с температурой определяется изменением kТ, а не величиной постоянных и других сомножителей. Давайте рассмотрим сейчас немного подробнее другой способ получения почти аналогичного результата для испарения. Чтобы получить (42.1), мы просто применили всегда справедливое при равновесии правило, но мало что поняли в существе явления. Поэтому невредно попытаться посмотреть детальнее, как происходит испарение. Можно описать его примерно так: молекулы пара непрерывно бомбардируют поверхность жидкости; при ударе они могут либо отскочить от поверхности, либо пробить ее. Что случается чаще, нам неизвестно, может быть, отношение этих исходов равно 50 к 50, а может быть и 10 к 90. Предположим, что поверхность пробивается всегда, потом мы посмотрим, к чему приводит предположение о более прочной поверхности. Тогда в каждый момент будет иметься определенное число атомов, сконденсировавшихся на поверхности жидкости. Число сконденсировавшихся молекул (число молекул, прошедших через площадку единичной площади) равно числу молекул в единице объема n, умноженному на скорость v. Эта скорость молекул связана с температурой; ведь известно, что в среднем 1/2mv2 равно 3/2 kТ. Поэтому v —какая-то средняя скорость. Конечно, нужно еще проинтегрировать по углам и сделать всякого рода усреднения, но результат прямо пропорционален корню из среднего квадрата скорости. Таким образом,
т. е. числу молекул, достигших единичной площадки и сконденсировавшихся. Но атомы жидкости непрерывно пляшут, и время от времени отдельные атомы выскакивают наружу. Теперь нам нужно выяснить, часто ли это происходит. При равновесии число молекул, выскочивших за 1 сек из жидкости, равно числу молекул, поступивших за это же время на ее поверхность. Ну, а много ли молекул выскакивает? Чтобы выскочить наружу, молекула должна как-то умудриться приобрести некоторую добавочную энергию, которая окажется больше, чем энергия ее соседок. И этот избыток энергии должен быть довольно большим, ведь наша молекула очень сильно притягивается к остальным молекулам жидкости. Обычно ей так и не удается преодолеть этого сильного притяжения, но иногда при столкновениях на ее долю выпадает излишек энергии. Шансы получить необходимую в нашем случае избыточную энергию W невелики, если W » kТ. Действительно, вероятность того, что атом приобретает энергию, большую чем W, равна ехр(—W/kT). Это общий принцип кинетической теории: шансы призанять энергию W сверх средней энергии равны е, возведенному в степень, показатель которой равен отношению W к kТ со знаком минус. Предположим, что некоторым молекулам удалось получить эту энергию. Теперь можно установить, сколько молекул покидает поверхность жидкости за 1 сек. Конечно, получение молекулой нужной энергии еще не означает, что испарение обеспечено. Ведь эта молекула может находиться слишком глубоко в жидкости, а если она даже и находится у поверхности, то может двигаться не туда.Число молекул, покидающих единичную площадку за 1 сек, — это примерно число молекул на единице площади вблизи поверхности, деленное на время, которое требуется молекуле для побега, и умноженное на вероятность ехр(—W/kT) готовности молекул к побегу, в том смысле, что они уже получили достаточное количество энергии. Предположим, что каждая молекула на поверхности жидкости занимает определенную площадку площади А. Тогда число молекул на единице поверхности жидкости равно 1/А. А много ли молекуле нужно времени, чтобы совершить свой побег? Если молекулы движутся с определенной средней скоростью v и должны пройти расстояние, равное, скажем, диаметру молекулы D (толщине наружного слоя), то время, нужное для преодоления этого расстояния, и есть время побега, если только молекула обладает достаточной энергией. Это время равно D/v. Таким образом, число испаряющихся молекул приблизительно равно
Заметим, что произведение площади каждой молекулы на толщину слоя приблизительно равно объему Va, отведенному каждой молекуле. Итак, для получения равновесия мы должны иметь Nc=Ne, или
Можно выкинуть из этого равенства скорости, потому что они равны; если даже специально отметить, что одна из них — скорость молекулы пара, а другая —скорость испаряющейся молекулы, — все равно они одинаковы, ведь мы знаем, что средняя кинетическая энергия обеих молекул (в одном направлении) равна 1/2kТ. Но можно сказать: «Нет! Нет! Ведь испаряются только особо быстрые молекулы. Только они приобрели достаточный избыток энергии». Не совсем так, потому что в тот момент, когда эти молекулы выскакивают из жидкости, они теряют этот избыток, преодолевая потенциальную энергию. Поэтому при подходе к поверхности они уже движутся с замедленной скоростью v! Точно так же обстояло дело с распределением молекулярных скоростей в атмосфере — в нижних слоях молекулы были определенным образом распределены по энергиям. Те из них, которые достигали более высоких слоев, распределялись по энергиям точно так же, потому что медленные молекулы вверх совсем не поднимались, а быстрые, поднявшись, двигались медленнее. Испаряющиеся молекулы распределены по скоростям так же, как молекулы, движущиеся в глубине жидкости — поистине поразительный факт. Во всяком случае, нет смысла пытаться столь строго обсуждать нашу формулу, потому что в ней есть и другие неточности; например, мы рассматривали вероятность отражения молекул от поверхности, а не их конденсации и т. д. Мы имеем дело лишь с грубым описанием скорости испарения и конденсации и видим, естественно, что плотность пара n изменяется так же, как и раньше, но теперь мы понимаем этот процесс много лучше, а раньше писали почти произвольную формулу. Более глубокое понимание позволит нам выяснить еще кое-что. Например, предположим, что мы откачиваем пар, причем так быстро, что пар удаляется практически с той же быстротой, с какой образуется (если наш насос очень хороший, а испарение происходит медленно). С какой скоростью будет происходить испарение, если температура жидкости Т будет поддерживаться постоянной? Предположим, что мы экспериментально уже измерили равновесную плотность пара и нам известно, сколько молекул в единице объема может быть в равновесии с жидкостью при заданной температуре. Теперь мы хотим узнать скорость испарения жидкости. Хотя мы ограничились лишь грубым анализом испарения, он все же дал нам сведения о числе прибывающих молекул пара, правда, с точностью до неизвестного коэффициента отражения. Поэтому мы можем использовать то обстоятельство, что при равновесии число покидающих пар молекул равно числу прибывающих молекул. Правда, пар откачивается и молекулы могут только покидать жидкость, но если оставить пар в покое, то установится равновесная плотность, при которой число прибывающих в жидкость молекул равно числу испаряющихся. Следовательно, легко видеть, что в этом случае число молекул, покидающих поверхность жидкости за 1 сек, равно произведению неизвестного коэффициента отражения R на число молекул, которые ежесекундно возвращались бы в жидкость, если бы пар не откачивался, потому что именно это число входит в уравнение баланса для испарения при равновесии:
Конечно, легче подсчитать число молекул, переходящих из пара в жидкость, потому что в этом случае не надо ничего предполагать о силах, как это нриходилось делать при подсчете числа покидающих жидкость молекул. Проще изменить путь рассуждений. СМОТРИТЕ ТАКЖЕ:Социальные комментарии Cackle |
При использовании материалов сайта ссылка на www.all-fizika.com обязательна.