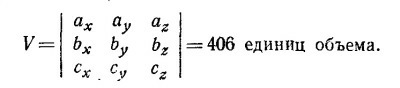Главная >> Фейнмановские лекции по физике >> Том 10 >> Задачи к томам I-IV Продолжение. Решения и ответы к задачам I-IV томов фейнмановских лекций по физике
 14.3. а) При перемещении частицы вдоль оси у работу совершает только y-компонента силы. Но Fу = Зх2 = 0 (х = 0 при движении вдоль оси у), поэтому и работа силы F равна нулю. 14.3. а) При перемещении частицы вдоль оси у работу совершает только y-компонента силы. Но Fу = Зх2 = 0 (х = 0 при движении вдоль оси у), поэтому и работа силы F равна нулю.
б) В этом случае нужно принимать во внимание только у-и z-компоненты силы F, так как перемещение перпендикулярно оси х. Однако Fy = 0 (х = 0 для всех точек плоскости у—z), поэтому работа силы F равна
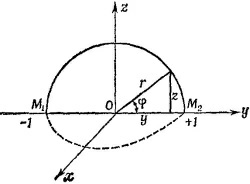
Как видно из рисунка, z = sin φ, y = cos φ,точке М1 соответствует значение угла φ = π, а точке М2—-значение φ = 0, поэтому
Однако это еще не означает, что сила F консервативна. Можно найти такие траектории частицы, для которых работа силы F не равна нулю. Например, если частица перемещается из точки М1 в точку М2 по окружности единичного радиуса, лежащей в плоскости х— у, работа силы F равна
Таким образом, работа при перемещении частицы из точки (0, —1, 0) в точку (0, 1, 0) зависит от пути перемещения, поэтому поле силы F неконсервативно.
14.4. 1. а) Кинетическая энергия частицы в конце пути равна работе, совершаемой силой F. Следовательно,
б) Из уравнения движения ma = Fx находим
Поэтому ускорение частицы в конце пути а = 2,5 м/сек2.
в) Мощность равна изменению кинетической энергии в единицу времени, т. е.
2. В этом случае удобнее непосредственно проинтегрировать уравнение движения ma =3+4t, откуда
(здесь учтено, что v= 0 при t = 0). Следовательно, при t = Зсек
14.5. Как было показано в «Лекциях» (вып. 1), поле и потенциал вне сферической оболочки равны полю и потенциалу точечного заряда, помещенного в центр сферы и равного по величине полному заряду оболочки. (Внутри оболочки поле равно нулю, т. е. потенциал не меняется от точки к точке.) Итак,
где R — радиус оболочки; q—ее полный заряд. Находим далее
14.6. Пусть А и В—радиусы соответственно внешней и внутренней сфер. Пользуясь результатом предыдущей задачи и принципом суперпозиции, вычислим потенциал на поверхности внешней сферы. Заряды, расположенные на внутренней сфере, создают на внешней сфере потенциал q/4πε0 A(q—заряд внутренней сферы), а заряды, расположенные на самой внешней сфере,— потенциал —q/4πε0A(напомним, что заряды сфер равны по величине и противоположны по знаку). Таким образом, потенциал внешней сферы равен нулю.
Займемся теперь внутренней сферой. Потенциал, создаваемый на ней ее собственными зарядами, равен q/4πε0B, а зарядами внешней сферы —q/4πε0A. Итак, разность потенциалов между сферами равна потенциалу внутренней сферы, так что
14.8. Мощность N связана с силой F и скоростью v соотношением N = Fv, так что F = N/v.
Из уравнения движения ma = F (m—масса автомобиля) имеем
14.9. Масса всего кабеля m=ML. В начальный момент времени центр тяжести кабеля находился на расстоянии L/4 от оси блока, в конечный—на расстоянии L/2.
Таким образом, изменение потенциальной энергии кабеля ΔU равно
Изменение кинетической энергии ΔЕ кабеля с учетом того, что вначале он покоился, равно
(Разумеется, все точки кабеля движутся с одной и той же скоростью v.)
Из закона сохранения энергии имеем ΔU = ΔЕ, откуда
14.10. Пусть вода вырывается из наконечника со скоростью v. Зная высоту подъема воды и угол наклона наконечника к горизонту, можно найти начальную скорость струи.
Действительно, Hмакс = (v2/2g) sin2 α, откуда
(здесь учтено, что α = 30°).
В единицу времени из шланга выбрасывается масса воды m = ρSv, где S —площадь поперечного сечения наконечника, а ρ — плотность воды. Полезная работа мотора в единицу времени затрачивается на поднятие этой массы воды на высоту h и на выбрасывание ее из шланга со скоростью v. Она равна
Подставляя численные, значения входящих в формулу для Р величин, получаем Р = 25 квт.
 14.11. Работа W, затрачиваемая атлетом на каждый бросок, равна mv2/2, где т—масса спортивного снаряда, a v—его начальная скорость. Таким образом, для вычисления W необходимо найти v. 14.11. Работа W, затрачиваемая атлетом на каждый бросок, равна mv2/2, где т—масса спортивного снаряда, a v—его начальная скорость. Таким образом, для вычисления W необходимо найти v.
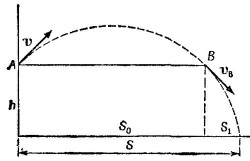
Обозначим через S дальность полета снаряда. Как видно из рисунка, S = S0+S1, где So—дальность полета снаряда, если бы он был брошен со скоростью v с поверхности Земли, a S1—горизонтальная дальность полета из точки В до соприкосновения снаряда с Землей. Имеем
(здесь учтено, что α = 45°), a S1 вычислим, рассматривая отдельно движение снаряда из точки В. Из закона сохранения энергии следует, что vB = v (сопротивлением воздуха пренебрегаем) и что vB направлена под углом 45° к горизонту. Поэтому S1 = (v/√2 ) t, где t —время падения снаряда из точки В на Землю, которое определяется из уравнения
Положительное решение этого квадратного (относительно t) уравнения есть
Подставляя в это выражение массы ядра, диска и копья и дальности их полета, выпишем работу, затраченную спортсменами при рекордных бросках этих снарядов:
14.12. При равномерном движении автомобиля по горизонтальному участку дороги вся мощность двигателя Р1 уходит на преодоление сил трения, поэтому P1 = Fтрv, откуда Fтр — P1/v.
При движении под углом θ к горизонту мощность двигателя расходуется как на преодоление сил тяготения, так и на преодоление сил трения. Следовательно, развиваемая мотором сила тяги F равна
При максимальном угле уклона мотор развивает максимально возможную мощность (Рмакс = 85 л. с). Таким образом,
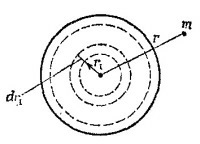 14.13. Разобьем все сферическое тело на большое число тонких слоев и проследим действие этих слоев на частицу массы m, находящуюся на расстоянии r от центра тела. В § 4 гл. 13 «Лекций» (вып. 1, стр. 239) было показано, что если масса m находится вне шарового слоя, то потенциальная энергия массы m такова, как если бы вся масса слоя собралась в его центре. Если r > R, то масса m является внешней по отношению ко всем слоям сферического тела, следовательно, ее потенциальная энергия W такова, как если бы вся масса тела собралась в его центре, т. е. 14.13. Разобьем все сферическое тело на большое число тонких слоев и проследим действие этих слоев на частицу массы m, находящуюся на расстоянии r от центра тела. В § 4 гл. 13 «Лекций» (вып. 1, стр. 239) было показано, что если масса m находится вне шарового слоя, то потенциальная энергия массы m такова, как если бы вся масса слоя собралась в его центре. Если r > R, то масса m является внешней по отношению ко всем слоям сферического тела, следовательно, ее потенциальная энергия W такова, как если бы вся масса тела собралась в его центре, т. е.
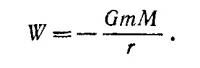 |
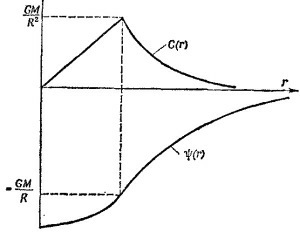 Потенциал Ψ гравитационного поля массы М связан с энергией W частицы m в этом поле соотношением W =mΨ, а с напряженностью С этого поля соотношением ∫Cds = —Ψ [см. «Лекции», вып. 1, стр. 254, формула (14.7)]. Потенциал Ψ гравитационного поля массы М связан с энергией W частицы m в этом поле соотношением W =mΨ, а с напряженностью С этого поля соотношением ∫Cds = —Ψ [см. «Лекции», вып. 1, стр. 254, формула (14.7)].
Поэтому в рассматриваемом случае Ψ = —GM/r, a напряженность C = GM/r2 и направлена к центру сферы.
Если r < R, масса m окажется внешней по отношению ко всем слоям, радиусы которых меньше r, и внутренней по отношению ко всем остальным слоям.
Поэтому потенциальная энергия массы m состоит из двух членов W1 и W2; W1—потенциальная энергия по отношению к внешним слоям и равна
W2 — потенциальная энергия массы ь по отношению к тем слоям, внутри которых она находится.
Рассмотрим отдельно один шаровой слой радиусом r1 и толщиной dr1. Потенциальная энергия тела m по отношению к этому слою dW′ постоянна и равна
Полную энергию массы m по отношению ко всем внешним слоям найдем, проинтегрировав dW′ по всем слоям
Отсюда легко получить потенциал и напряженность гравитационного поля внутри тела:
14.14. Скорость груза m непосредственно перед падением его на чашку весов, определенная из закона сохранения энергии, равна v=√2gh. Скорость v1 чашки с грузом после удара найдем из закона сохранения количества движения
где m1—масса чашки.
В наинизшей точке (находящейся на h1 ниже первоначального положения чашки) полная кинетическая и потенциальная энергия чашки и груза перейдет в потенциальную энергию растянутой пружины:
где k —упругость пружины, а /0 — ее удлинение перед падением груза на чашку, I0 = m1g/k= 1,6 см.
После несложных преобразований полученное уравнение приводится к виду
(здесь введено обозначение h0 = mg/k = 3,2 см). Решая это уравнение, находим
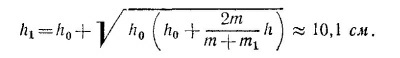 |
Таким образом, груз m опустится вниз на расстояние h+h1 = 19,1 см.
14.15. Пyсть к пружине приложена сила F0. Величина растяжения пружины х0 определяется из условия kx0 = F0.
Растянем теперь пружину на величину х относительно нового положения равновесия. Сила, приложенная к пружине, равна теперь k (x+xo)= kx0+kx = Fo+kx. Видно, что добавочная сила, растягивающая пружину на расстояние х из нового положения равновесия, такая же, как если бы пружина растягивалась на х из ненапряженного состояния. Отсюда следует, что жесткость пружины осталась неизменной.
14.16. Если тележка проходит верхнюю точку петли «на пределе», почти не касаясь путевого полотна, сила давления на нее со стороны полотна, естественно, равна нулю. Таким образом, в этой точке на тележку действует только сила тяжести mg. Ускорение тележки в наивысшей точке равно v2/R=g, поэтому ее скорость в этой точке равна √gR . Если тележка начала движение с высоты Н над петлей без начальной скорости, то из закона сохранения энергии следует
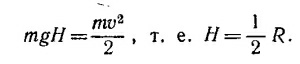 |
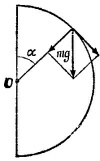 14.17. Пусть, тело срывается в точке сферы, радиус-вектор которой образует угол α с вертикалью. В этой точке сила нормального давления тела на сферу равна нулю. Поэтому проекция ускорения силы тяжести на радиус (g cosα) равна центростремительному ускорению. Таким образом, 14.17. Пусть, тело срывается в точке сферы, радиус-вектор которой образует угол α с вертикалью. В этой точке сила нормального давления тела на сферу равна нулю. Поэтому проекция ускорения силы тяжести на радиус (g cosα) равна центростремительному ускорению. Таким образом,
Решая совместно эти два уравнения, получим cos α=2/3.
Таким образом, тело сорвется в точке, отстоящей от вершины сферы по вертикали на расстоянии 1/3 R. По дуге сферы тело пройдет при этом путь S = αR =0,85R.
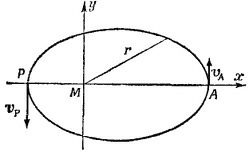 14.18. Поместим начало системы координат в фокус эллипса (там же находится масса М), а ось х направим вдоль его большой оси. Полная энергия тела массы m, являющаяся суммой его кинетической и потенциальной энергий E = mv2/2—GMm/r, сохраняется и Е есть просто константа, не зависящая ни от времени, ни от r. Поэтому удобно вычислить ее для таких положений тела m, в которых его радиус-вектор и скорость особенно просто выражаются через параметры эллипса. 14.18. Поместим начало системы координат в фокус эллипса (там же находится масса М), а ось х направим вдоль его большой оси. Полная энергия тела массы m, являющаяся суммой его кинетической и потенциальной энергий E = mv2/2—GMm/r, сохраняется и Е есть просто константа, не зависящая ни от времени, ни от r. Поэтому удобно вычислить ее для таких положений тела m, в которых его радиус-вектор и скорость особенно просто выражаются через параметры эллипса.
Такими положениями являются апогей и перигей, отмеченные точками А и Р на рисунке. Для них rA = а(1+е), rP = а(1—е). Скорости vA и vP перпендикулярны оси х (так как они направлены по касательной к эллипсу). Кроме того, как было показано в задаче 7.7, в соответствии со вторым законом Кеплера эти скорости связаны между собой соотношением
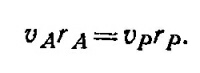 |
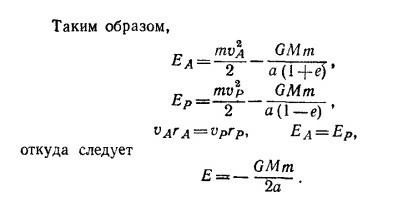 |
14.19. а) Эллипс можно получить из окружности радиусом b, если увеличить масштаб вдоль одной из осей координат в а/b раз. При увеличении масштаба вдоль одной из осей площади фигур увеличиваются во столько же раз, поэтому площадь эллипса равна
(а—длина большой полуоси).
б) Вычислим скорость планеты в апогее (см. решение задачи 14.18):
в) Используя результат задачи 14.18, выразим длину большой полуоси орбиты через полную энергию и массу планеты:
Подставляя ее, в формулу для периода, получаем
Отсюда и следует утверждение, что орбиты всех тел, у которых на единицу массы приходится одинаковая энергия, соответствуют равным периодам обращения (период зависит только от отношения m к | Е |).
14.20. Уменьшение кинетической энергии корабля по мере его удаления от Земли происходит за счет увеличения его потенциальной энергии, т. е.
Здесь v0 и v—скорости корабля соответственно около Земли (R = 6500 км) и на расстоянии r≈ 106 км.
Если бы корабль покинул Землю с первой космической скоростью v1, то на очень больших расстояниях от Земли он двигался бы с очень маленькой скоростью, т. е.
14.21. Обозначим через v скорость космического корабля относительно Солнца в момент прекращения работы двигателей, а через v′—его скорость «на выходе». Потенциальная энергия корабля обусловлена притяжением Земли и Солнца. Когда корабль находится около Земли, его потенциальная энергия равна
где m, М и MO—массы соответственно корабля, Земли и Солнца; R — радиус Земли; R1 — радиус земной орбиты, которую для простоты будем считать круговой. Из закона сохранения энергии следует
где v1 —вторая космическая скорость (см. предыдущую задачу), а из условия стационарности земной орбиты следует
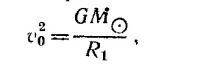 |
где v0—орбитальная скорость Земли.
Таким образом, v2=v12+2v02+v′2, откуда v = 47 км/сек. Скорость корабля относительно Земли будет минимальной, когда он запущен в направлении орбитального движения Земли. Тогда
vмин = v — v0 = 17 км/сек.
14.22. Скорость корабля относительно Земли максимальна, если корабль запущен по касательной к орбите Земли в направлении, противоположном движению Земли. В этом случае
vмакс = v + v0 = 77 км/сек.
14.23. Период обращения планеты вокруг Солнца зависит только от величины большой полуоси эллипса орбиты. Из того, что периоды обращения Земли и космического корабля совпадают, следует равенство больших полуосей орбит Земли и
корабля.
Величиной большой полуоси полностью определяется и другая характеристика планеты—полная энергия на единицу массы (см. задачу 14.18). Поэтому, когда Земля и космический корабль находятся на одинаковом расстоянии от Солнца (и, следовательно, имеют по отношению к Солнцу одинаковую потенциальную энергию на единицу массы), их скорости относительно Солнца одинаковы по величине.
Заметим, что мы не учли в этих рассуждениях притяжения корабля Землей. Будем считать для начала, что корабль берет старт не с Земли, а из некоторой периферийной точки «околоземного пространства», где потенциал тяготения Солнца начинает превышать потенциал тяготения Земли. Оценим, насколько такая точка удалена от Земли. Потенциал Солнца (–GMO/R1) и потенциал Земли (–GM/R) сравниваются, если R = R1M/MO. Так как M/MO≈2,5- 10–5, если удалиться от Земли, скажем, на десятитысячную радиуса земной орбиты, потенциал Солнца будет превышать потенциал Земли (а «с точки зрения Солнца» Земля и корабль будут по-прежнему в одном и том же месте!).
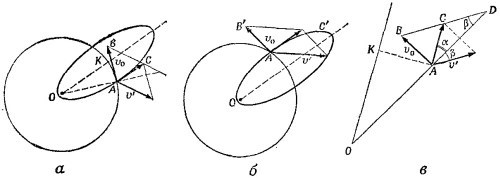
Существуют четыре варианта запуска. Два из них изображены на рисунке (а и б). Рассчитаем вариант а (как более экономный). Так как корабль в перигее подходит очень близко к Солнцу, его скорость при пересечении земной орбиты (которую здесь и далее считаем круговой) практически параллельна линии, проходящей через фокусы орбиты корабля. Найдем угол а. Из прямоугольного треугольника OAK (на рисунке в) cosα = (a—rр)/а = 0,99 (а —большая полуось орбиты корабля, равная радиусу орбиты Земли). Из треугольника ABC находим BC = v′—скорость запуска корабля из периферии околоземного пространства. Учитывая, что AB = AC=v0 (v0—орбитальная скорость Земли), имеем
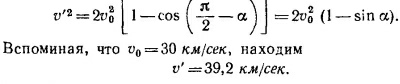 |
Угол β, под которым запущен корабль относительно линии Земля—Солнце, найдем из треугольника ABD (замечая, что < AВС = β +α):
Учтем теперь, что корабль стартует с поверхности Земли. Вспоминая задачу 14.21, находим, что истинная скорость запуска v = √v′2+v12, где v1—вторая космическая скорость.
Итак, v ≈42 км/сек.
14.24. Представим себе сначала, что в сферическом теле нет никакой полости. Ускорение силы тяжести в точке Р равно в этом случае
Выделим теперь внутри тела часть вещества, занимающую тот же объем и положение, что и фигурирующая в условии полость. Согласно принципу суперпозиции, ускорение в точке Р можно представить в виде суммы двух членов: ускорения, обусловленного веществом, занимающим выделенный объем
и интересующим нас ускорением а, связанным с притяжением тела с полостью. Так как все три ускорения направлены вдоль одной прямой PC, то
2 ПРОСТРАНСТВО ВРЕМЯ ДВИЖЕНИЕ
К главе 15. Специальная теория относительности
15.1. Так как уравнения, связывающие х′, у′, z′, t′ с х, у, z, t, линейны, выразить нештрихованные координаты через штрихованные не представляет труда. Имеем
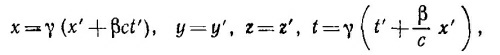 |
где введены обозначения β = u/c, γ = (√1 — β2)–1.
Эти формулы можно было получить и не решая уравнений, а просто заменив в исходных преобразованиях Лоренца и на —и и поменяв местами координаты х, у, z, t и х′, у′, z′, t′ (так как система х, у, z движется относительно х′, у′, z′ со скоростью —и).
15.2. Рассмотрим работу «световых часов» в неподвижной и движущейся системах координат. Для наблюдателя, который движется вместе с часами, луч света от одного конца стержня до другого и обратно проходит за промежуток времени t = 2L/c, где L — длина стержня.
Как же представляется работа этих часов для неподвижного наблюдателя? Прежде всего ему кажется, что длина стержня не L, a L′ = L √1—u2/с2 (и — скорость движения часов). Если время движения светового сигнала от одного конца стержня до другого в направлении движения стержня равно t1, то за это время сам прибор сместился на расстояние ut1 поэтому свет прошел расстояние не L, a L′ +ut1 так что ct1 = L′+ut1 и t1 = L`/(c—и). Для прохождения света от одного конца стержня до другого против движения самого стержня требуется время t2 причем ct2 = L′—ut2 и t2 = L′ /(с+и). Общее время движения света равно
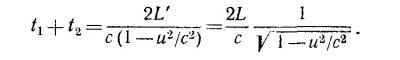 |
Таким образом, свету понадобится большее время, чтобы пройти из конца в конец движущийся стержень, нежели неподвижный стержень, т. е. движущиеся часы будут отставать по сравнению с неподвижными. Обратим внимание, что это отставание точно такое же, как и в случае, когда часы ориентированы поперек движения (см. §4 г л .15 «Лекций», вып. 2, стр. 12).
15.3. С точки зрения земного наблюдателя время жизни мюона такое, что за это время, двигаясь со скоростью и, он успевает пройти путь /, поэтому
Время жизни т мезона в его собственной системе координат есть
пройденный же им путь (вернее, толщина слоя «прошедшей» мимо него атмосферы) равен
15.4. а) Для производства энергии Е необходимо превратить в энергию вещество массой m = Е/с2. В нашем случае m= 86 кг.
б) В каждом акте синтеза двух атомов дейтерия в гелий выделяется энергия
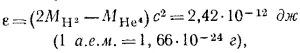 |
т. е. в энергию превращается 0,0155 а.е.м. Но как раз два атома дейтерия входят в молекулу тяжелой воды, масса которой равна 20,0294 а.е.м., поэтому можно сказать, что только 0,77-10–3 часть тяжелой воды превращается в энергию. Отсюда следует, что годовое потребление тяжелой воды равно М = (86/0,77)· 103кг, а ее ежесекундный расход М/т = 3,5 г/сек (т—число секунд в году).
15.5. Если W — мощность солнечного излучения, поглощаемая в земной атмосфере, то энергия, выделяемая на Солнце в 1 сек, равна E = 4πD2W, где D — расстояние от Земли до Солнца. Следовательно, выделяемой в единицу времени энергии соответствует масса т = Е/с2. Реакция образования гелия из обычного водорода заключается в том, что четыре атома водорода (mH = 1,0081 а.е.м.) объединяются в атом гелия (mНе =4,0039а.е.м.) Хотя при этом образуются две частицы с массой покоя, отличной от нуля, они в дальнейшем также превращаются в излучение (позитроны, встречаясь с электронами, «пропадают», образуя γ-кванты). Поэтому можно утверждать, что часть массы водорода
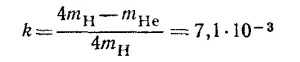 |
отвечает энергии, выделившейся в результате реакции.
Таким образом, в 1 сек на Солнце «сгорает» масса водорода
что составляет примерно 3·10–17% массы Солнца.
15.6. Сила и импульс в релятивистской механике связаны между собой таким же образом, как и в ньютоновской, F = d(mv)/dt, только масса в релятивистском случае не постоянна, а выражается через массу покоя как m = m0/√1 — v2/с2, т. е. зависит от скорости движения частицы. Итак,
Таким образом, действующая на частицу сила F = m0c2/b постоянна.
15.7. а) Единица длины световой год — это то расстояние, которое луч света проходит за один год; она равна сτ, где с = 3·108 м/сек—скорость света, а т = 3,15 ·107—число секунд в году. Поэтому
б) Сила тяжести, которую чувствуют космонавты,— это сила, прижимающая их к кораблю. Корабль, конечно, действует на них с такой же силой. Согласно условию задачи, эти силы постоянны и, таким образом, движение всех предметов внутри корабля — это движение под действием постоянной силы. Такое движение изучалось в предыдущей задаче. Поэтому, чтобы сразу использовать результаты этой задачи, представим силу в нашем случае в виде F = m0с2/b. Константу b определим из условия т0с2/b = m0g0. Вычисления будем проводить в такой системе единиц, где расстояния измеряются световыми годами, а время — годами. В этой системе единиц скорость света равна 1 свет, год/год. Результаты вычислений дают:
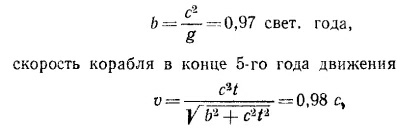 |
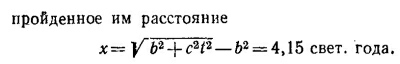 |
К главе 16. Релятивистская энергия и релятивистский импульс
16.1. Рассмотрим систему координат х, у, z, t и штрихованную систему х′, у′, z′, t′, движущуюся относительно исходной со скоростью и в положительном направлении оси x. Формулы задачи 15.1 для связи нештрихованных координат со штрихованными запишем в виде
где β = u/с, γ–1 = √1 — β2. Беря дифференциалы от правых и левых частей этих соотношений, получаем преобразования Лоренца в дифференциальной форме:
Ho dx/dt=vx—скорость в неподвижной системе координат, a dx′/dt′ =vx′—скорость в движущейся системе координат, поэтому
Если vx′ = 0, то получаем формулу (16.7), приведенную в «Лекциях» (вып. 2, стр. 30) для vy..
16.2. Чтобы найти величину скорости в движущейся системе координат, выразим дифференциалы штрихованных координат через дифференциалы нештрихованных координат: dx′ = γ(dx — βcdt), dy`=dy, dz` = dz, dt` =γ [dt— (β/c)dx]. Разделив dx` на dt`, найдем скорость в подвижной системе координат
(Конечно, эту формулу можно написать сразу, изменив только знак скорости и в соответствующей формуле предыдущей задачи.)
Вычислим дифференциал dvx′:
Разделив dvx′ на dt′ и учитывая, что ax′ = dvx′/dt′, a = dvx/dt, получим
16.3. Из треугольника скоростей (см. «Лекции», вып. 2, стр. 34) следует, что скорости v, w и и связаны между собой соотношением v2 = u2+w2(1—u2/с2), поэтому
Чтобы доказать приведенную в тексте формулу, остается только внимательно проделать следующие выкладки:
16.4. Рассмотрим неупругое столкновение частиц в такой системе координат, в которой они налетали бы друг на друга с одинаковой скоростью w. Очевидно, эта система координат сама движется с той же скоростью w в направлении движущейся частицы. Так как в неподвижной системе скорость налетающей частицы равна 4/5 с, то
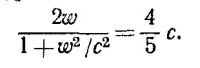 |
Мы могли бы решить это уравнение относительно w и убедиться, что w = 1/2c, но мы не будем. этого делать, так как в § 3 гл. 16 «Лекций» (вып. 2, стр. 30) было показано, что в результате сложения двух скоростей по 1/2c каждая получаем скорость, равную 4/5 с. Поэтому w = 1/2с.
В выбранной таким образом движущейся системе координат образовавшаяся составная частица неподвижна, а ее масса есть M0 = 2mw = 4m0/ √3 . Таким образом, составная частица с массой покоя М0 движется в исходной системе координат со скоростью 1/2с.
16.5. В системе координат, в которой протоны ускорителя и мишени налетают друг на друга с одинаковыми скоростями, скорость протонов w определяется из следующего условия: 2mр/ √ 1 —w2/с2 =4mр, откуда w=(√ 3/2) с. Скорость протонов в лабораторной системе координат (в этой системе частицы мишени покоятся) равна
Кинетическая энергия налетающих протонов есть разность между их полной энергией и энергией покоя, т. е.
К главе 17. Пространство-время
17.1. Из соотношения между энергией и импульсом E2—р2 = тр2 (в системе единиц, где с= 1) следует, что Е≈ р, так как Е и р намного больше тр. Из определения же релятивистского импульса частицы находим
(здесь учтено, что тр/р«1 и использована приближенная формула 1/(1 +х) ≈ 1—х). Таким образом, скорость протона такой большой энергии отличается от скорости света только в 20-м знаке! Поэтому с точки зрения земного наблюдателя такой протон пересечет Галактику по диаметру за 105 лет. С точки зрения протона такое путешествие займет всего
17.2. Здесь нужны только вычисления. Масса покоя электрона me= 9,11·10-28 г, с = 3·108 м/сек, поэтому тес2 =
= 81,99·10-15 дж. Посмотрев в справочник, можно убедиться, что 1 эв =1,6·10-19 дж, так что
17.3. Из закона сохранения импульса следует, что трехмерные импульсы μ-мезона рμ и нейтрино pv равны и направлены в противоположные стороны. Из закона сохранения энергии вытекает, что сумма полной энергии мезона и нейтрино равна энергии покоя π-мезона, т. е. Еv+ Еμ= тπ (в системе единиц, где с=1).
Так как Ev = pv (масса покоя нейтрино равна нулю) и
Кинетическую энергию μ-мезона найдем как разность его полной энергии и энергии покоя:
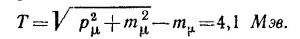 |
Кинетическая энергия нейтрино равна его полной энергии и равна импульсу.
17.4. В задаче 12.14 было показано, что заряженная частица в магнитном поле В движется по окружности радиусом R, причем R=mv/qB. Этот результат сохраняется и в релятивистском случае, поскольку при таком движении меняется только направление скорости, а не ее величина.
Так как mv = p, то p = qBR. Здесь q измеряется в кулонах, В — в вебер/м2, R — в метрах, а р — в кг·м/сек. Учитывая, что 1 вебер/м2 = 104 гс, заряд частицы равен q = Zqe, а qe=1,6·10-19 к и 1 кг·м/сек = (1,6/с)·10-25 Мэв, получаем р = 3·10-2 ZBR. В этой формуле единицы измерения физических величин следующие: р — Мэв, В — гауссы, R — метры, Z—безразмерная величина.
17.5. а) Радиус магнита циклотрона должен быть не меньше радиуса кривизны траектории частицы предельной энергии в данном магнитном поле. Используя результаты предыдущей задачи, имеем R =p ·102/3ZB. Импульс релятивистской частицы равен √ Е2— m02, а ее полная энергия Е есть сумма кинетической энергии Т и энергия покоя E = T+m0, поэтому
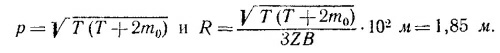 |
б) Частота ускоряющего электрического поля должна совпадать с частотой обращения частицы (см. задачу 12.5), т. е.
В этом выражении m измеряется в Мэв, В — в гауссах, а время — в метрах. Таким образом, частота ускоряющего поля в конце ускорения равна
в) В начале ускорения частиц частота электрического поля должна быть
К главе 18. Двумерные вращения
18.1. а) По определению момента силы τ = xFy— yFx=140 нм. Но момент мы можем представить и в виде
где р — плечо силы, a Ft —тангенциальная (перпендикулярная к r) составляющая силы. Из этих двух равенств находим
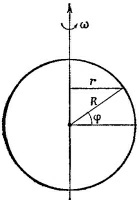 18.2. За счет суточного вращения Земли каждая точка земной поверхности приобретает зависящую от широты φ скорость v = ωr = ωR cos φ (см. рисунок), где ω—угловая скорости вращения Земли. 18.2. За счет суточного вращения Земли каждая точка земной поверхности приобретает зависящую от широты φ скорость v = ωr = ωR cos φ (см. рисунок), где ω—угловая скорости вращения Земли.
В Лос-Анджелесе (φо = 34°, см. географическую карту) v = Rω cos φ0. Широту искомой точки земной поверхности найдем из уравнения
18.3. Найдем сначала проекции силы на оси координат (ось у направим вверх по прямой ОР, а ось х—направо по АВ). Так как в равновесии сумма всех сил, действующих на тело, равна нулю, имеем
Учтем теперь, что полный момент силы (будем вычислять его относительно точки О) также должен равняться нулю. Прежде всего ясно, что точка приложения силы F должна лежать слева от точки О; необходимо, чтобы сила F вращала пластинку против часовой стрелки. Приравнивая нулю полный момент сил, найдем / —расстояние от точки О до точки приложения силы
Итак, удерживающая сила величиной F = √ Fx2 + Fy2 ≈ 20,5 ньютон приложена левее точки O на 0,34 м и направлена параллельно силе, приложенной в точке О.
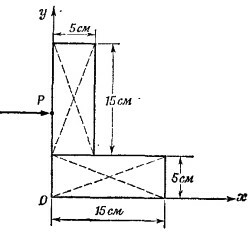 18.4. Уголок не вращается после удара в том случае, если удар произведен по линии, проходящей через его центр масс (момент количества движения относительно ц. м., переданный при ударе, в этом случае равен нулю). Поэтому ОР = у0, где у0 —ордината центра масс. Так как толщина горизонтальной и вертикальной сторон уголка постоянна, центры масс сторон уголка совпадают с их геометрическими центрами. Как видно из рисунка, ордината центра масс горизонтальной стороны у1 = 2,5 см, а вертикальной у2= 12,5 см. Ординату центра масс всего уголка найдем по формуле 18.4. Уголок не вращается после удара в том случае, если удар произведен по линии, проходящей через его центр масс (момент количества движения относительно ц. м., переданный при ударе, в этом случае равен нулю). Поэтому ОР = у0, где у0 —ордината центра масс. Так как толщина горизонтальной и вертикальной сторон уголка постоянна, центры масс сторон уголка совпадают с их геометрическими центрами. Как видно из рисунка, ордината центра масс горизонтальной стороны у1 = 2,5 см, а вертикальной у2= 12,5 см. Ординату центра масс всего уголка найдем по формуле
18.5. Условия равновесия всей фермы в целом таковы:
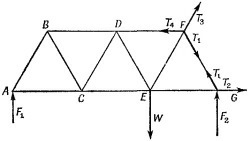 Стержень GF испытывает сжатие, a EG — растяжение. Их нагрузки равны соответственно T1, и Т2. Но F2/T1 = cos 30°, откуда Стержень GF испытывает сжатие, a EG — растяжение. Их нагрузки равны соответственно T1, и Т2. Но F2/T1 = cos 30°, откуда
Из равновесия в узле F имеем Т1+Т3 + Т4 = 0 (Т3 и Т4 — напряжения в стержнях EF и DF). Проектируя это равенство на вертикальную ось, получаем
Приравнивая затем нулю сумму проекций на горизонтальную ось, находим
Таким образом, стержень FD сжат, его напряжение 4W/З√ З.
18.6. а) Момент инерции стержня в системе координат, ось х которой направлена вдоль стержня, а начало совпадает с концом стержня, равен
б) Если ось проходит не через конец стержня, а через его середину, то интегрирование следует проводить в пределах не от 0 до L, а от —L/2 до L/2:
Этот же результат можно получить из теоремы о параллельном переносе оси, относительно которой вычисляется момент инерции: / = /ц.м.+ md2 ( d — расстояние между осями, а /ц.м. — момент инерции относительно оси, проходящей через центр масс). Искомый момент инерции есть как раз /ц.м.,так как центр масс стержня находится на середине L:
 в) Если цилиндр тонкостенный, то вся его масса m находится на расстоянии r от оси вращения, поэтому, согласно определению момента инерции, I = тr2. в) Если цилиндр тонкостенный, то вся его масса m находится на расстоянии r от оси вращения, поэтому, согласно определению момента инерции, I = тr2.
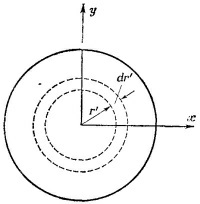
г) Для вычисления момента инерции сплошного цилиндра разобьем его на большое число тонкостенных полых цилиндров. На рисунке показан один такой цилиндр радиусом r′ и толщиной dr′. Момент инерции этого цилиндра [см. пункт (в)] d/ = r′2dm′, где
(т — масса цилиндра, H—высота цилиндра).
Таким образом, момент инерции сплошного цилиндра вычисляется так:
18.7. Когда цилиндр поворачивается на угол φ, груз опускается на расстояние rφ, поэтому ускорение груза а связано с угловым ускорением цилиндра d2φ/dt2:
18.8. а) Поскольку момент внешних сил равен нулю, момент количества движения груза сохраняется, т. е. Отсюда скорость груза в конечном состоянии
б) Работа внешней силы равна изменению кинетической энергии груза, поэтому
в) Пусть F — сила, которую необходимо приложить к нити, чтобы удержать шарик на расстоянии r. При виртуальном перемещении dr эта сила выполняет работу [см. пункт (б)]
[Мы пренебрегли членом ~ (dr)2.] Сокращая dr, получаем F=mv2/r, что, конечно, и следовало ожидать.
18.9. Момент количества движения планеты является суммой двух членов L1+L2, L1 связан с движением планеты по орбите (L1=mvR), a L2 — с ее вращением вокруг своей оси (L2 = /ω). Учитывая, что для движения по круговой орбите v2/R = GM/R2 (считаем, что центральное тело очень тяжелое), получаем
Величина L2 для всех реальных случаев оказывается гораздо меньше L1.
Рассмотрим теперь систему Земля — Луна. В момент количества движения этой системы дают вклад следующие движения: движение Луны относительно ц. м. системы Земля—Луна, вращение Луны вокруг своей оси, движение Земли относительно ц. м. системы, вращение Земли вокруг своей оси.
Вспомним теперь, что период вращения Луны вокруг своей оси равен периоду ее движения по орбите. Поэтому
где R — радиус лунной орбиты, а rл —радиус-Луны. Таким образом, L1Л»L2Л, и этой последней величиной можно пренебречь. Далее, поскольку период обращения Земли и Луны вокруг ц. м. системы одинаков, а расстояние до ц. м. обратно пропорционально массам
т. е. вклад орбитального движения Земли в момент количества движения также очень мал. Оценим теперь вклад вращения Земли вокруг своей оси. Имеем
Следовательно, момент количества движения системы Земля — Луна равен приближенно
Из-за приливов, тормозящих вращение Земли, длина суток медленно увеличивается, т. е. уменьшается угловая скорость вращения, а с ней и момент количества движения Земли L2З. Так как полный момент количества движения системы Луна — Земля должен оставаться постоянным, момент количества движения Луны L1Л должен медленно возрастать, компенсируя уменьшение L2З.
Увеличение L1Л (см. выражение для этой величины) возможно только в случае увеличения расстояния между Луной и Землей.
Энергия системы Земля — Луна состоит из кинетической и потенциальной энергий Луны и кинетической энергии вращения Земли (мы опять пренебрегли кинетической энергией вращения Луны и движения Земли по орбите как малыми величинами).
Как было показано в задаче 14.18 (стр. 200), полная энергия Луны равна
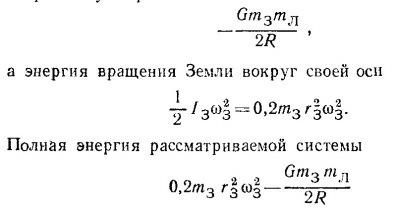 |
положительна, в чем можно убедиться, подставив вместо букв соответствующие числа. В предельном случае (далеком будущем), когда Земля полностью прекратит вращаться вокруг своей оси (ω3 = 0), полная энергия системы Земля — Луна станет отрицательной (—GmЗmЛ/2R0), R0—расстояние между Луной и Землей при ω3 = 0; это означает, что полная механическая энергия системы Земля — Луна уменьшается по мере удаления Луны от Земли. Это и понятно, ведь часть механической энергии вследствие приливного трения превращается в теплоту.
18.10. Когда подвешиваются грузы W1 и W2, силы, действующие в шарнирах, изменяются. Нас будут интересовать только эти добавки. Силы, которые действовали в шарнирах раньше, как раз такие, чтобы рама с грузом Wc оставалась в равновесии, поэтому, рассматривая только добавки, мы можем не учитывать ни веса рамы, ни груза Wc. Выясним условие равновесия планки АВ. Суммарный момент силы, действующий на эту планку,
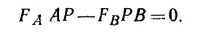 |
Здесь FA и FB — вертикальные составляющие силы в шарнирах А и В (момент горизонтальных составляющих сил равен нулю). Аналогично,
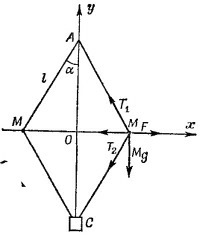 18.11. По условию задачи машина должна отключаться, когда АС достигнет значения √2·30 см, т. е. когда угол α = 45°. В системе координат, вращающейся вместе с регулятором, массы М находятся в равновесии. На каждую из них действует центробежная сила F и реакции стержней T1 и Т2 (направление сил показано на рисунке). 18.11. По условию задачи машина должна отключаться, когда АС достигнет значения √2·30 см, т. е. когда угол α = 45°. В системе координат, вращающейся вместе с регулятором, массы М находятся в равновесии. На каждую из них действует центробежная сила F и реакции стержней T1 и Т2 (направление сил показано на рисунке).
Используем условие равновесия массы М. Из равенства нулю суммы горизонтальных составляющих сил получаем
Наконец, условие равновесия массы С записывается как
18.12. Мощность, необходимая для вращения вала, равна мощности сил трения, т. е.
где v—скорость масс т, v = ωr.
Сила трения каждой колодки равна произведению коэффициента трения на величину силы, прижимающей колодку к цилиндру, т. е.
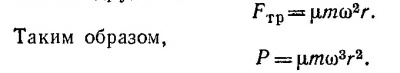 |
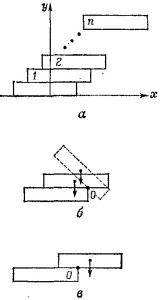 18.13. Поместим начало системы координат в середину основания нижнего бруска. Обозначим через х1, х2, ....,хn координаты центров масс соответствующих брусков (см. фиг. а). Очевидно, что сооружение из брусков опрокинется, когда координата х0 центра масс всей системы брусков, лежащих на нижнем, выйдет за его основание, т. е. когда х0 ≥ L/2 (знак равенства соответствует неустойчивому равновесию). 18.13. Поместим начало системы координат в середину основания нижнего бруска. Обозначим через х1, х2, ....,хn координаты центров масс соответствующих брусков (см. фиг. а). Очевидно, что сооружение из брусков опрокинется, когда координата х0 центра масс всей системы брусков, лежащих на нижнем, выйдет за его основание, т. е. когда х0 ≥ L/2 (знак равенства соответствует неустойчивому равновесию).
Поясним это, рассмотрев условие равновесия двух брусков, лежащих друг на друге. Пусть сначала бруски расположены так, как это показано на фиг. б. Повернем верхний брусок относительно точки О на малый угол Δφ по часовой стрелке и отпустим его. Как будет двигаться брусок дальше?
Сила веса бруска создает относительно точки О вращающий момент т =mg[(L/2)—/] (m —масса бруска, / —длина выступающей части торца), который стремится повернуть брусок в исходное положение. Это и означает, что в положении, показанном на фиг. б, брусок находится в равновесии. По мере стремления / к L/2 величина вращающего момента убывает. Наконец, т = 0 при / =L/2. Теперь достаточно отклонить верхний брусок на бесконечно малый угол, чтобы брусок начал вращаться по часовой стрелке; это означает, что верхний брусок находится в положении неустойчивого равновесия. Разумеется, при / > L/2 (см. фиг. в), возникает вращающий момент τ = mg (I — L/2), опрокидывающий верхний брусок.
Вычислим координату центра масс всех брусков, лежащих на нижнем. Очевидно,
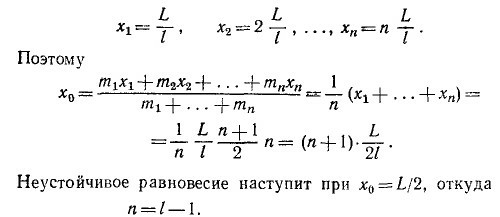 |
Следовательно, максимальное число брусков, которые можно уложить указанным способом, равно /.
К главе 19. Центр масс; момент инерции
19.1. Энергия, затраченная механизмом К, равна изменению кинетической энергии вращения системы, т. е.
где /0 и /1—моменты инерции «квадратной» и «крестообразной» систем, а ω1 — конечная угловая скорость вращения. Момент инерции системы складывается из моментов инерции стержней и момента инерции внутреннего механизма.
Пользуясь теоремой о параллельном переносе оси, находим, что момент инерции одного стержня относительно оси О равен в начальном состоянии (4/3) mL2, а в конечном (m/3)L2 Поэтому
Конечную угловую скорость вращения ω1 находим из закона сохранения момента количества движения (механизм, складывающий стержни,— внутренний!)
19.2. а) Пусть нить закручена на угол θ. Чтобы удержать ее в этом положении, к нити нужно приложить внешние силы, момент которых т был бы равен упругому моменту нити с обратным знаком, т. е. т = kθ.
При дальнейшем закручивании нити на малый угол Δθ, как было показано в гл. 18 «Лекций» (вып. 2, стр. 53), внешние силы совершают работу ΔW =т·Δθ. Нить, закрученная на фиксированный угол θ0, обладает, таким образом, потенциальной энергией U, равной по величине работе внешних сил, поворачивающих нить от ненапряженного состояния (θ = 0) до угла θ0, т. е.
б) В момент разряда конденсатора на рамку действует момент τ=nAB|dqldt|, в результате чего рамка начнет вращаться с угловой скоростью ω = L/I, где L—момент количества движения рамки, / —ее момент инерции. Величину L найдем, интегрируя уравнение
от t= 0 до момента окончания разряда конденсатора, что дает L = nABq0 (q0—первоначальный заряд конденсатора). Когда катушка отклоняется на максимальный угол и останавливается, начальная кинетическая энергия рамки
переходит в потенциальную энергию закрученной нити, на которой подвешена катушка, U =1/2 kθ2макс, т. е.
т. е. максимальный угол поворота рамки пропорционален начальному заряду конденсатора.
19.3. Момент инерции сложной фигуры равен сумме моментов инерции ее частей. Поэтому момент инерции проволоки, вычисленной относительно оси, проходящей через точку А, не зависит от угла θ и равен ML2/12.
19.4. Для моментов инерции пластинок относительно осей, проходящих через точки А и В, можем написать
Приведенное в тексте равенство выполняется, если r32 = r22 — r12, т. е. когда r1 r2, r3 образуют прямоугольный треугольник, причем гипотенузой является r2.
19.5. Объем фигуры вращения равен произведению длины дуги, описываемой центром масс плоской фигуры, на площадь этой фигуры. В нашем случае
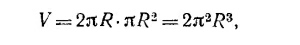 |
так как центр масс однородного круга лежит в его геометрическом центре.
19.6. Энергия, затрачиваемая на достижение данной угловой скорости ω0 из неподвижного состояния, равна кинетической энергии вращающегося тела. Эта энергия тем меньше, чем меньше момент инерции тела (ω0 фиксировано!).
Для любого тела / = /ц.м.+ Мd2, где /ц.м.—момент инерции относительно оси, проходящей через центр масс; d — расстояние от этой оси до параллельной ей оси вращения. Очевидно, что /мин отвечает d = 0. Таким образом, ось вращения должна проходить через центр масс, который находится на расстоянии М2L/(М1+М2) от конца невесомого стержня, несущего массу М1.
19.7. Пусть диск с прижатыми грузиками вращается с угловой скоростью ω. Его момент количества движения L0 равен [(МR2/2) + 2mR2]·ω
В момент срыва нитей с крючков Н и Н′ диск вращается с угловой скоростью ω1, определяемой из закона сохранения момента количества движения:
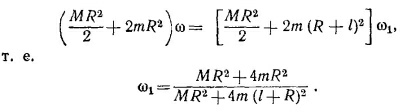 |
После отделения грузиков диск продолжает вращаться с той же угловой скоростью ω1, так что угловая скорость диска уменьшается в n раз, если
19.8. В неподвижной системе координат ху на тело действует сила F. Тело будет двигаться в этой системе координат согласно уравнениям движения mx = Fx; my =Fy. При повороте системы координат на угол θ = ωt координаты преобразуются следующим образом:
Компоненты силы в штрихованной системе координат имеют вид
Первые два члена в каждом выражении есть компоненты истинной силы F в повернутой системе координат, третьи слагаемые —компоненты силы Кориолиса, и последние — центробежной силы.
19.9. Уравнение движения для центра масс шара
Скорость той точки шара, которая соприкасается с плоскостью, равна vц.м.—ωR. Когда эта скорость обращается в нуль, шар начинает катиться без проскальзывания. Это произойдет через промежуток времени t от начала движения, равный
 и его скорость к этому моменту vt = v—μgt = 5/7v. и его скорость к этому моменту vt = v—μgt = 5/7v.
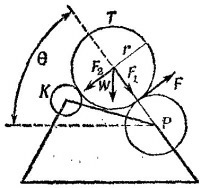
19.10. Вес W валика разложим на две составляющие: силу нормального давления его на вал Р, равную F1 = Mg sin θ, и перпендикулярную к ней, F2 = Mg cos θ.
Контакт между передающим валиком Т и барабаном К не будет теряться в том случае, если «сила тяги» F, приложенная со стороны печатного вала Р к валику Т (как раз и обусловливающая вращение валика Т), меньше или равна F2, т. е.
(знак равенства соответствует нулевому давлению Т на K).
Уравнение вращательного движения для валика Т, когда он не давит на барабан К, имеет вид /A1 = Fr, или (Mr2/2) A1 — Mg cos θr (здесь через A1= dω/dt обозначено угловое ускорение валика Т), так как
19.11. Обозначим массу первой секции через m, тогда массы соответствующих квадрантов будут:
Поскольку каждая из секций однородна, то центры масс их расположены одинаково относительно самих секций. Если координаты центров масс секций (х1у1)... (x4y4), то положение центра масс всего тела вычисляется по формулам
Из соойбражений симметрии ясно, что центр масс каждой из секций лежит на биссектрисе соответствующего прямого угла, на одинаковом расстоянии от начала координат.
Обозначим координаты центра масс первой секции через а:
Уравнение прямой, проходящей через две точки (0, 0) и (X, У), есть
19.12. Пусть М — масса диска с отверстием; m —масса вырезанной части диска; х —абсцисса центра масс диска с отверстием.
Поскольку центр масс сплошного диска находится в его центре, то
19.13. Выберем систему координат, как рекомендовано в условии задачи. Так как проволока расположена симметрично относительно оси х, то, очевидно, yц. м. = 0. По определению центра масс
эта формула является обобщением приведенной в «Лекциях» формулы
Масса проволоки бесконечно малой длины dl равна ρdl, где ρ = M/L—масса единицы длины проволоки, поэтому
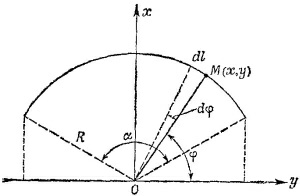 Вычислять такой интеграл в прямоугольной системе координат довольно громоздко. Эти вычисления значительно упрощаются, если заметить, что для произвольной точки проволоки, радиус-вектор которой образует угол φ с осью у, x = R cos φ, a dl = Rdφ(см. рисунок). Чтобы были учтены все точки проволоки, угол φ должен пробегать`"значения от (π—α)/2 до (π+α)/2, где α=L/R —угол между радиусами-векторами концов проволоки. Таким образом, Вычислять такой интеграл в прямоугольной системе координат довольно громоздко. Эти вычисления значительно упрощаются, если заметить, что для произвольной точки проволоки, радиус-вектор которой образует угол φ с осью у, x = R cos φ, a dl = Rdφ(см. рисунок). Чтобы были учтены все точки проволоки, угол φ должен пробегать`"значения от (π—α)/2 до (π+α)/2, где α=L/R —угол между радиусами-векторами концов проволоки. Таким образом,
Этот же результат может быть получен из теоремы Паппа (см. «Лекции», вып. 2, стр. 72—73). При вращении проволоки вокруг оси у получается шаровой пояс площадью
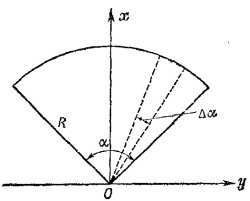 19.14. Разобьем сектор на большое число секторов с вершинами в точке О и очень малым центральным углом Δα. Каждый такой сектор с большой точностью можно рассматривать как равнобедренный треугольник, центр масс которого лежит на высоте, на расстоянии 2/3 R от его вершины. 19.14. Разобьем сектор на большое число секторов с вершинами в точке О и очень малым центральным углом Δα. Каждый такой сектор с большой точностью можно рассматривать как равнобедренный треугольник, центр масс которого лежит на высоте, на расстоянии 2/3 R от его вершины.
Таким образом, задача о нахождении центра масс сектора свелась к нахождению центра масс дуги окружности радиусом 2/3R с углом раствора α, т. е. к предыдущей задаче. В такой же системе координат, как и в задаче 19.13,
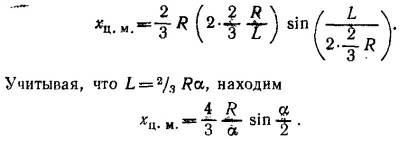 |
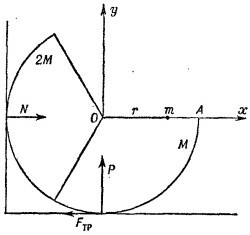 19.15. а) Определим положение центра масс, получившегося после склеивания тела. Как было показано в предыдущей задаче, центр масс сектора лежит на его биссектрисе на расстоянии 4/3(R/α) sin (α/2) от центра окружности. (В нашем случае это расстояние равно √ 3 см, так как R = π см и α = 2π/3.) Биссектриса сектора массы 2M направлена горизонтально, поэтому координаты центра масс этого тела х2 = —√ 3 см, y2 = 0. Биссектриса сектора массы М образует угол 30° с вертикалью, так что координаты x1и у1центра масс этого сектора равны: 19.15. а) Определим положение центра масс, получившегося после склеивания тела. Как было показано в предыдущей задаче, центр масс сектора лежит на его биссектрисе на расстоянии 4/3(R/α) sin (α/2) от центра окружности. (В нашем случае это расстояние равно √ 3 см, так как R = π см и α = 2π/3.) Биссектриса сектора массы 2M направлена горизонтально, поэтому координаты центра масс этого тела х2 = —√ 3 см, y2 = 0. Биссектриса сектора массы М образует угол 30° с вертикалью, так что координаты x1и у1центра масс этого сектора равны:
Следовательно, координаты центра масс тела, получившегося после склеивания двух частей, есть
Рассмотрим силы, действующие на тело. Это сила тяжести, приложенная в центре масс тела, силы давления пола и стенки Р и N и сила трения о пол FTp. Эти силы приложены в точках соприкосновения тела со стенкой и полом и направлены так, как это показано на рисунке. Так как тело находится в равновесии, геометрическая сумма всех сил равна нулю; сумма моментов этих сил, например относительно точки О, также равна нулю. Это дает
Поскольку M = 1 кг, тело давит на стенку с силой 3 √3/2π кГ.
б) Если поместить на линию ОА массу m на расстоянии r от точки О, то система останется в равновесии, если будут равны друг другу моменты сил веса составного тела и шарика относительно точки соприкосновения тела и пола:
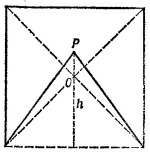 19.16. Поскольку вся фигура, подвешенная в точке Р, находится в равновесии независимо от ее положения, точка Р является ее центром масс. 19.16. Поскольку вся фигура, подвешенная в точке Р, находится в равновесии независимо от ее положения, точка Р является ее центром масс.
Пусть высота вырезанного треугольника равна h. Его центр масс находится на расстоянии 2/3 h от Р. Центр масс полученной фигуры и вырезанного треугольника находится в точке О, следовательно (см. задачу 19.12),
Так как по смыслу задачи h < a, в качестве решения выбираем меньший корень квадратного уравнения, т. е. h = 0,63 а.
19.17. а) На катушку действует сила веса, направленная вертикально вниз, и сила натяжения нити Т, направленная по нити. Катушка не будет раскачиваться, если нет горизонтальных сил, т. е. если нить вертикальна,
б) Запишем уравнение движения катушки:
для поступательного
здесь а —ускорение центра масс катушки, ε —ее угловое ускорение. Учитывая, что ε = а/r и l = MR2, уравнения движения перепишем в виде
19.18. а) Из закона сохранения момента количества движения
С другой стороны, чтобы удержать вращающуюся с угловой скоростью ω массу m на расстоянии х от оси вращения, необходимо приложить к нити силу
что равно разности кинетических энергий системы в конечном и начальном состояниях.
в) В системе координат, вращающейся вместе со столом, скорость тележки увеличивается благодаря действию центробежной силы, так что в этой системе кинетическая энергия тележки в точке R равна вычисленной в пункте (б) работе W, т. е.
К главе 20. Вращение и пространство
20.1. Векторное произведение двух векторов а и b можно записать в виде
20.2. Направим ось z вдоль вектора ω (т. е. вдоль оси вращения твердого тела), а начало координат поместим в произвольной точке на оси вращения. Вычислим векторное произведение ω x r (r—радиус-вектор точки Р тела) в этой системе координат
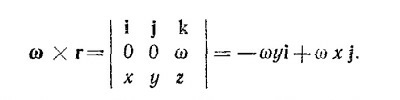 |
Полученный вектор лежит в плоскости ху и перпендикулярен вектору r′ (х, у), модуль его равен ω√x2+y2=ωr′. Так как r′ — расстояние точки Р до оси вращения, вычисленное векторное произведение есть не что иное, как скорость точки Р твердого тела, т. е. vр = ω x r.
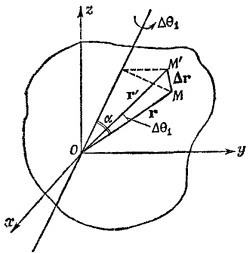
20.3. Пусть тело повернется на некоторый очень малый угол Δθ1 вокруг оси 1, проходящей через начало координат. Введем вектор Δθ1, величина которого равна Δθ1, а направление совпадает с осью вращения, т.е. Δθ1 = Δθ1 n1 (n1—-единичный вектор вдоль оси вращения). Очевидно, что при таком повороте радиус-вектор r произвольной точки М станет равным r′=r + Δr. Величина приращения радиуса-вектора равна (см. рисунок) r sin α Δθ1 вектор Δr направлен перпендикулярно r и оси вращения (т. е. Δθ1), поэтому, вспоминая определение векторного произведения,
 |
Если произведен еще один поворот на малый угол Δθ2 вокруг другой оси, проходящей через начало координат, то новый радиус-вектор той же точки М (обозначим его r″) может быть выражен через r как
В последнем выражении отброшены бесконечно малые второго порядка.
Таким образом, два последовательных поворота на углы Δθ1 и Δθ2 вокруг разных осей эквивалентны одному повороту на угол
вокруг оси, направление которой совпадает с направлением вектора Δθ1 + Δθ2. Аналогично для N поворотов на малые углы Δθ¡ имеем
 Рассматривая угловую скорость как вектор, направленный вдоль оси вращения, модуль которого равен изменению угла в единицу времени, записываем ω¡= Δθ¡/Δt. Поэтому вращение тела с несколькими угловыми скоростями эквивалентно вращению с одной угловой скоростью Рассматривая угловую скорость как вектор, направленный вдоль оси вращения, модуль которого равен изменению угла в единицу времени, записываем ω¡= Δθ¡/Δt. Поэтому вращение тела с несколькими угловыми скоростями эквивалентно вращению с одной угловой скоростью
20.4. Обозначим через r′ координаты частиц в системе ц. м. Очевидно,
20.5. а) Объем V параллелепипеда равен произведению площади основания на высоту: V = SH.
Обозначим угол между сторонами А и В основания через α. Величина площади основания равна
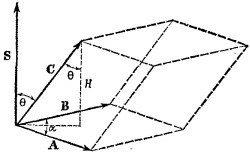 Вектор S = A x B направлен перпендикулярно векторам А и В, т. е. его направление совпадает с нормалью к основанию. Вектор S = A x B направлен перпендикулярно векторам А и В, т. е. его направление совпадает с нормалью к основанию.
Если угол между S и С равен θ, то V = SH = SC cosθ = C·S = |C(A х В)|.
б) Параллелепипед определен тремя векторами:
а = 10i—5j+3k, b = 3i—4j + 7k, c=— 5i— 6j + 3k.
Следовательно, его объем есть абсолютная величина детерминанта
Продолжение (начиная с 20.6). Решения и ответы к задачам I-IV томов фейнмановских лекций по физике
СМОТРИТЕ ТАКЖЕ:
Социальные комментарии Cackle
|




 14.3. а) При перемещении частицы вдоль оси у работу совершает только y-компонента силы. Но Fу = Зх2 = 0 (х = 0 при движении вдоль оси у), поэтому и работа силы F равна нулю.
14.3. а) При перемещении частицы вдоль оси у работу совершает только y-компонента силы. Но Fу = Зх2 = 0 (х = 0 при движении вдоль оси у), поэтому и работа силы F равна нулю.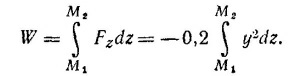
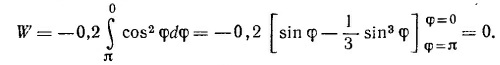
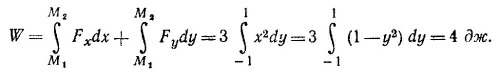
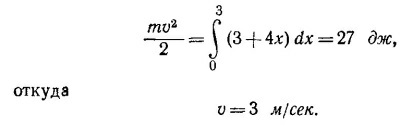
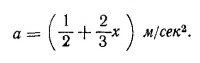
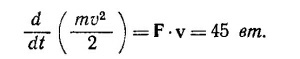
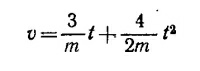
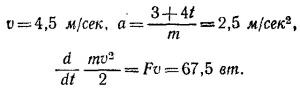
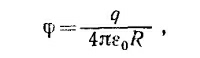
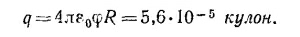
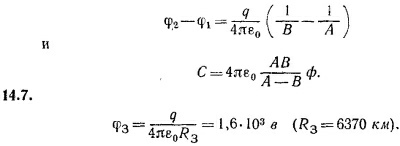
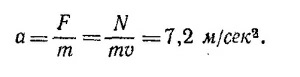
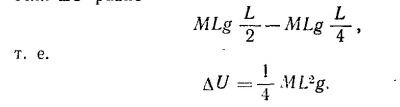
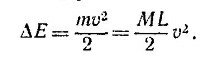
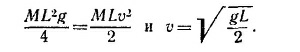
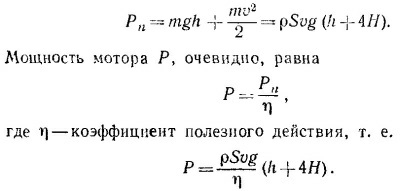
 14.11. Работа W, затрачиваемая атлетом на каждый бросок, равна mv2/2, где т—масса спортивного снаряда, a v—его начальная скорость. Таким образом, для вычисления W необходимо найти v.
14.11. Работа W, затрачиваемая атлетом на каждый бросок, равна mv2/2, где т—масса спортивного снаряда, a v—его начальная скорость. Таким образом, для вычисления W необходимо найти v.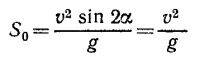
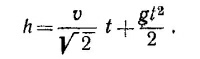

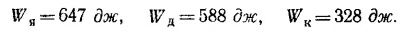
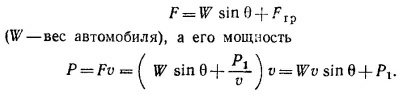
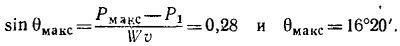
 14.13. Разобьем все сферическое тело на большое число тонких слоев и проследим действие этих слоев на частицу массы m, находящуюся на расстоянии r от центра тела. В § 4 гл. 13 «Лекций» (вып. 1, стр. 239) было показано, что если масса m находится вне шарового слоя, то потенциальная энергия массы m такова, как если бы вся масса слоя собралась в его центре. Если r > R, то масса m является внешней по отношению ко всем слоям сферического тела, следовательно, ее потенциальная энергия W такова, как если бы вся масса тела собралась в его центре, т. е.
14.13. Разобьем все сферическое тело на большое число тонких слоев и проследим действие этих слоев на частицу массы m, находящуюся на расстоянии r от центра тела. В § 4 гл. 13 «Лекций» (вып. 1, стр. 239) было показано, что если масса m находится вне шарового слоя, то потенциальная энергия массы m такова, как если бы вся масса слоя собралась в его центре. Если r > R, то масса m является внешней по отношению ко всем слоям сферического тела, следовательно, ее потенциальная энергия W такова, как если бы вся масса тела собралась в его центре, т. е.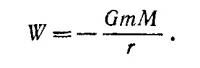
 Потенциал Ψ гравитационного поля массы М связан с энергией W частицы m в этом поле соотношением W =mΨ, а с напряженностью С этого поля соотношением ∫Cds = —Ψ [см. «Лекции», вып. 1, стр. 254, формула (14.7)].
Потенциал Ψ гравитационного поля массы М связан с энергией W частицы m в этом поле соотношением W =mΨ, а с напряженностью С этого поля соотношением ∫Cds = —Ψ [см. «Лекции», вып. 1, стр. 254, формула (14.7)].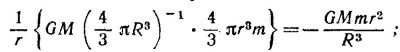
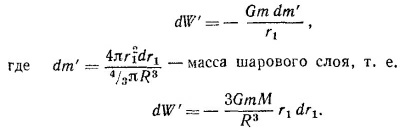
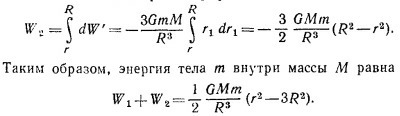
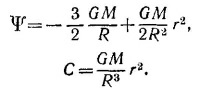
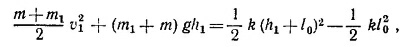
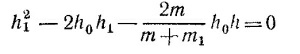
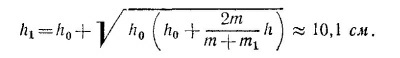
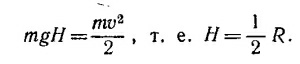
 14.17. Пусть, тело срывается в точке сферы, радиус-вектор которой образует угол α с вертикалью. В этой точке сила нормального давления тела на сферу равна нулю. Поэтому проекция ускорения силы тяжести на радиус (g cosα) равна центростремительному ускорению. Таким образом,
14.17. Пусть, тело срывается в точке сферы, радиус-вектор которой образует угол α с вертикалью. В этой точке сила нормального давления тела на сферу равна нулю. Поэтому проекция ускорения силы тяжести на радиус (g cosα) равна центростремительному ускорению. Таким образом,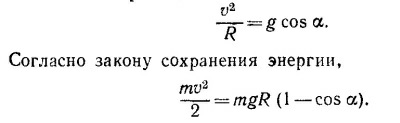
 14.18. Поместим начало системы координат в фокус эллипса (там же находится масса М), а ось х направим вдоль его большой оси. Полная энергия тела массы m, являющаяся суммой его кинетической и потенциальной энергий E = mv2/2—GMm/r, сохраняется и Е есть просто константа, не зависящая ни от времени, ни от r. Поэтому удобно вычислить ее для таких положений тела m, в которых его радиус-вектор и скорость особенно просто выражаются через параметры эллипса.
14.18. Поместим начало системы координат в фокус эллипса (там же находится масса М), а ось х направим вдоль его большой оси. Полная энергия тела массы m, являющаяся суммой его кинетической и потенциальной энергий E = mv2/2—GMm/r, сохраняется и Е есть просто константа, не зависящая ни от времени, ни от r. Поэтому удобно вычислить ее для таких положений тела m, в которых его радиус-вектор и скорость особенно просто выражаются через параметры эллипса.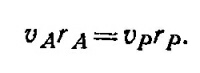
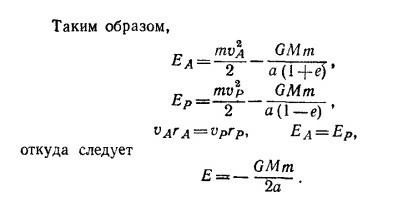
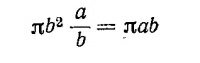

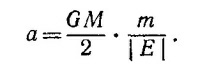
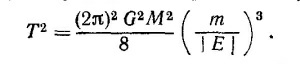
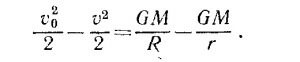
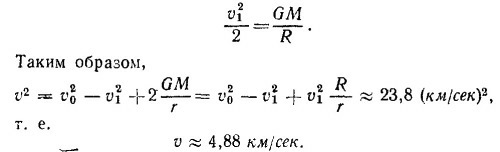
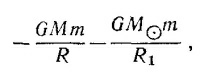
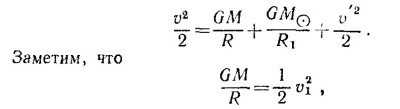
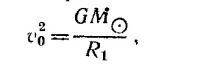
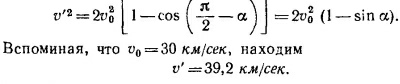
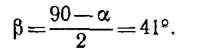
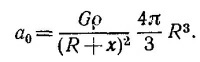
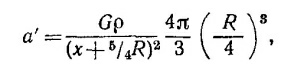
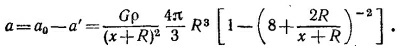
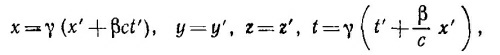
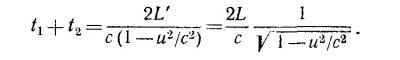
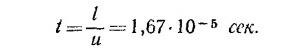
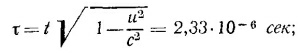
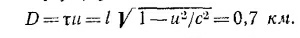
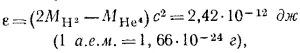
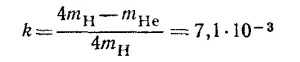
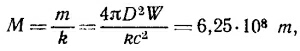
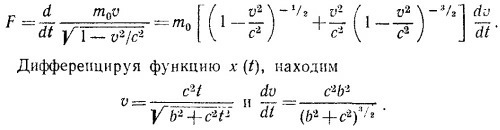
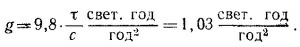
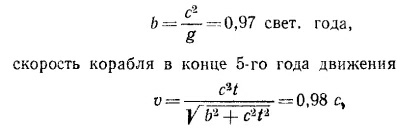
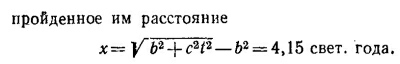
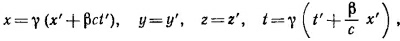
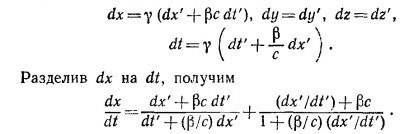
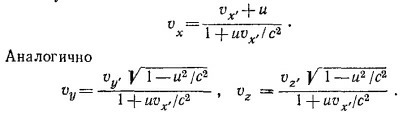
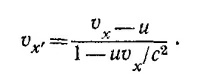
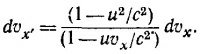
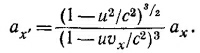
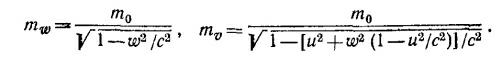
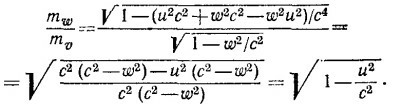
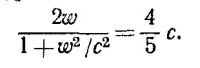
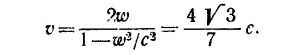
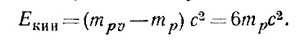
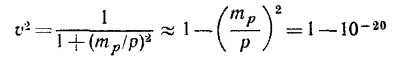

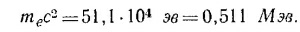
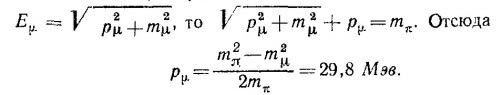
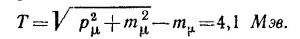
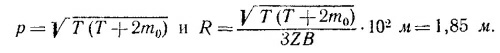
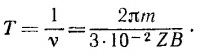
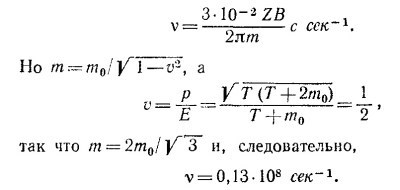
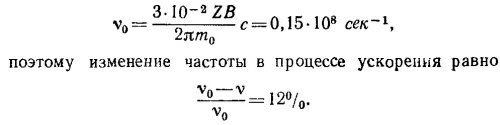
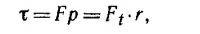
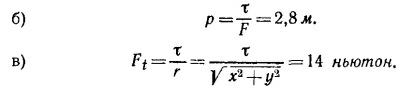
 18.2. За счет суточного вращения Земли каждая точка земной поверхности приобретает зависящую от широты φ скорость v = ωr = ωR cos φ (см. рисунок), где ω—угловая скорости вращения Земли.
18.2. За счет суточного вращения Земли каждая точка земной поверхности приобретает зависящую от широты φ скорость v = ωr = ωR cos φ (см. рисунок), где ω—угловая скорости вращения Земли.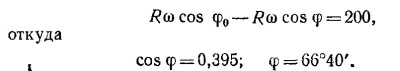
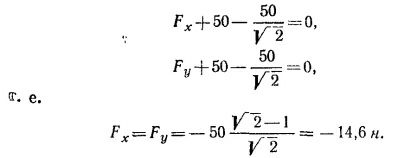
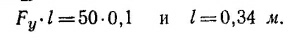
 18.4. Уголок не вращается после удара в том случае, если удар произведен по линии, проходящей через его центр масс (момент количества движения относительно ц. м., переданный при ударе, в этом случае равен нулю). Поэтому ОР = у0, где у0 —ордината центра масс. Так как толщина горизонтальной и вертикальной сторон уголка постоянна, центры масс сторон уголка совпадают с их геометрическими центрами. Как видно из рисунка, ордината центра масс горизонтальной стороны у1 = 2,5 см, а вертикальной у2= 12,5 см. Ординату центра масс всего уголка найдем по формуле
18.4. Уголок не вращается после удара в том случае, если удар произведен по линии, проходящей через его центр масс (момент количества движения относительно ц. м., переданный при ударе, в этом случае равен нулю). Поэтому ОР = у0, где у0 —ордината центра масс. Так как толщина горизонтальной и вертикальной сторон уголка постоянна, центры масс сторон уголка совпадают с их геометрическими центрами. Как видно из рисунка, ордината центра масс горизонтальной стороны у1 = 2,5 см, а вертикальной у2= 12,5 см. Ординату центра масс всего уголка найдем по формуле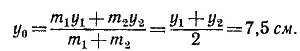
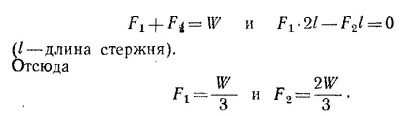
 Стержень GF испытывает сжатие, a EG — растяжение. Их нагрузки равны соответственно T1, и Т2. Но F2/T1 = cos 30°, откуда
Стержень GF испытывает сжатие, a EG — растяжение. Их нагрузки равны соответственно T1, и Т2. Но F2/T1 = cos 30°, откуда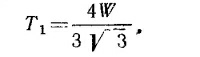
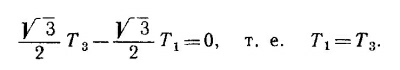
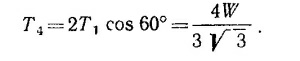
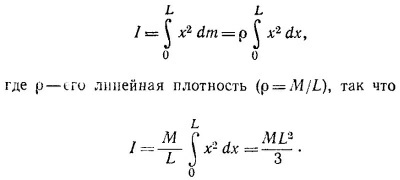
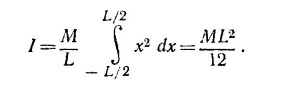
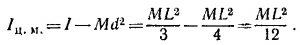
 в) Если цилиндр тонкостенный, то вся его масса m находится на расстоянии r от оси вращения, поэтому, согласно определению момента инерции, I = тr2.
в) Если цилиндр тонкостенный, то вся его масса m находится на расстоянии r от оси вращения, поэтому, согласно определению момента инерции, I = тr2.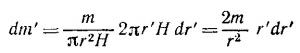
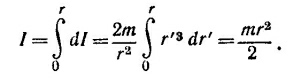

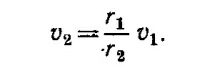
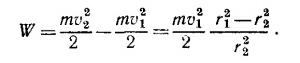
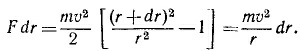
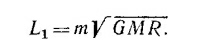
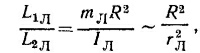
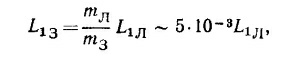
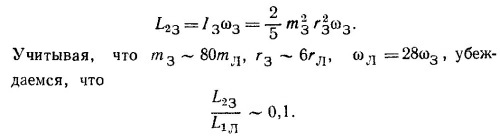
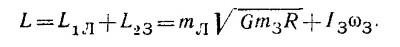
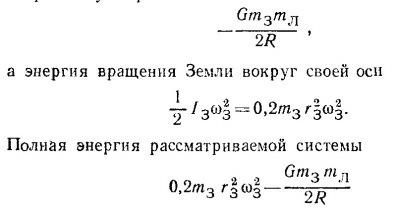
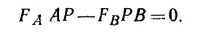

 18.11. По условию задачи машина должна отключаться, когда АС достигнет значения √2·30 см, т. е. когда угол α = 45°. В системе координат, вращающейся вместе с регулятором, массы М находятся в равновесии. На каждую из них действует центробежная сила F и реакции стержней T1 и Т2 (направление сил показано на рисунке).
18.11. По условию задачи машина должна отключаться, когда АС достигнет значения √2·30 см, т. е. когда угол α = 45°. В системе координат, вращающейся вместе с регулятором, массы М находятся в равновесии. На каждую из них действует центробежная сила F и реакции стержней T1 и Т2 (направление сил показано на рисунке).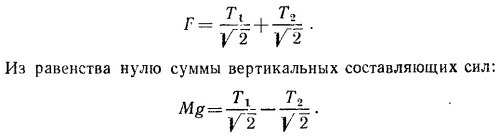
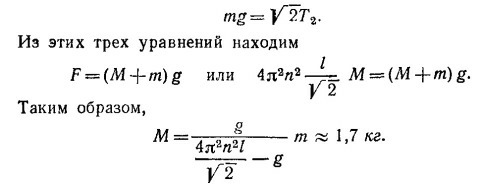
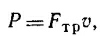
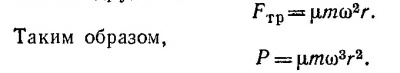
 18.13. Поместим начало системы координат в середину основания нижнего бруска. Обозначим через х1, х2, ....,хn координаты центров масс соответствующих брусков (см. фиг. а). Очевидно, что сооружение из брусков опрокинется, когда координата х0 центра масс всей системы брусков, лежащих на нижнем, выйдет за его основание, т. е. когда х0 ≥ L/2 (знак равенства соответствует неустойчивому равновесию).
18.13. Поместим начало системы координат в середину основания нижнего бруска. Обозначим через х1, х2, ....,хn координаты центров масс соответствующих брусков (см. фиг. а). Очевидно, что сооружение из брусков опрокинется, когда координата х0 центра масс всей системы брусков, лежащих на нижнем, выйдет за его основание, т. е. когда х0 ≥ L/2 (знак равенства соответствует неустойчивому равновесию).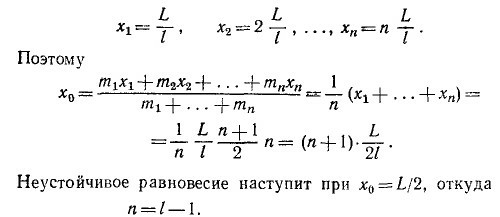
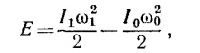
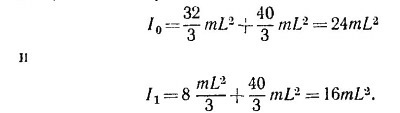
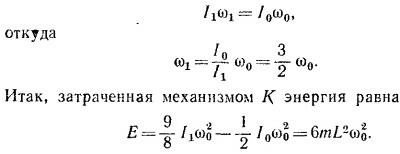
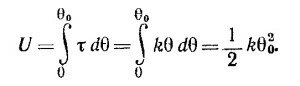
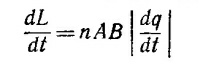
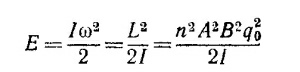

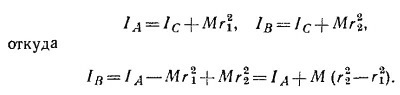
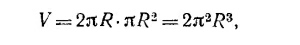
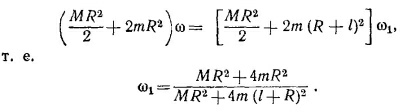
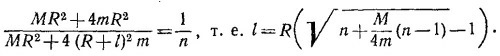
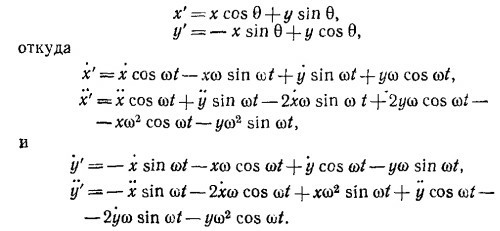
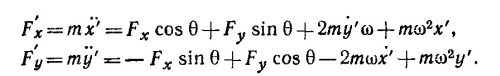
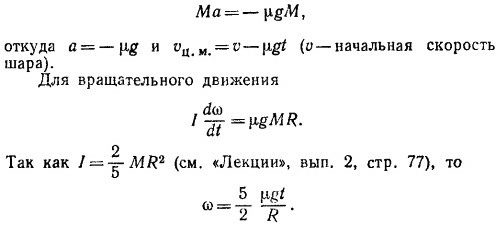
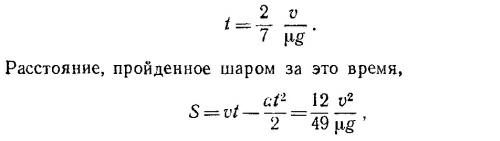
 и его скорость к этому моменту vt = v—μgt = 5/7v.
и его скорость к этому моменту vt = v—μgt = 5/7v.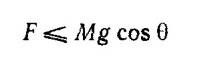
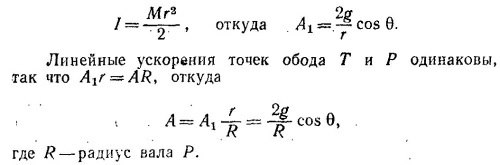
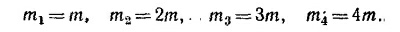
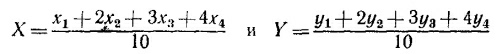
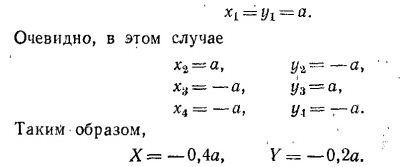
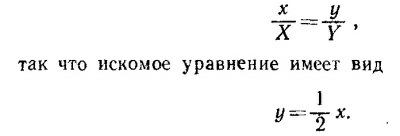
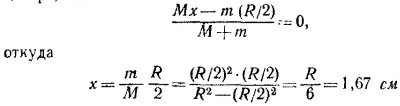
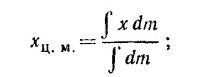
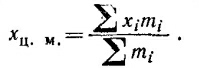
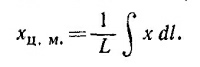
 Вычислять такой интеграл в прямоугольной системе координат довольно громоздко. Эти вычисления значительно упрощаются, если заметить, что для произвольной точки проволоки, радиус-вектор которой образует угол φ с осью у, x = R cos φ, a dl = Rdφ(см. рисунок). Чтобы были учтены все точки проволоки, угол φ должен пробегать`"значения от (π—α)/2 до (π+α)/2, где α=L/R —угол между радиусами-векторами концов проволоки. Таким образом,
Вычислять такой интеграл в прямоугольной системе координат довольно громоздко. Эти вычисления значительно упрощаются, если заметить, что для произвольной точки проволоки, радиус-вектор которой образует угол φ с осью у, x = R cos φ, a dl = Rdφ(см. рисунок). Чтобы были учтены все точки проволоки, угол φ должен пробегать`"значения от (π—α)/2 до (π+α)/2, где α=L/R —угол между радиусами-векторами концов проволоки. Таким образом,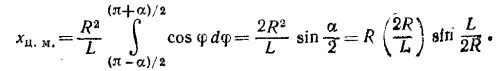
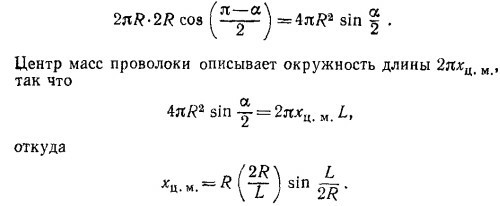
 19.14. Разобьем сектор на большое число секторов с вершинами в точке О и очень малым центральным углом Δα. Каждый такой сектор с большой точностью можно рассматривать как равнобедренный треугольник, центр масс которого лежит на высоте, на расстоянии 2/3 R от его вершины.
19.14. Разобьем сектор на большое число секторов с вершинами в точке О и очень малым центральным углом Δα. Каждый такой сектор с большой точностью можно рассматривать как равнобедренный треугольник, центр масс которого лежит на высоте, на расстоянии 2/3 R от его вершины.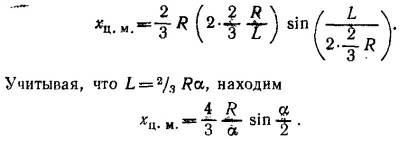
 19.15. а) Определим положение центра масс, получившегося после склеивания тела. Как было показано в предыдущей задаче, центр масс сектора лежит на его биссектрисе на расстоянии 4/3(R/α) sin (α/2) от центра окружности. (В нашем случае это расстояние равно √ 3 см, так как R = π см и α = 2π/3.) Биссектриса сектора массы 2M направлена горизонтально, поэтому координаты центра масс этого тела х2 = —√ 3 см, y2 = 0. Биссектриса сектора массы М образует угол 30° с вертикалью, так что координаты x1и у1центра масс этого сектора равны:
19.15. а) Определим положение центра масс, получившегося после склеивания тела. Как было показано в предыдущей задаче, центр масс сектора лежит на его биссектрисе на расстоянии 4/3(R/α) sin (α/2) от центра окружности. (В нашем случае это расстояние равно √ 3 см, так как R = π см и α = 2π/3.) Биссектриса сектора массы 2M направлена горизонтально, поэтому координаты центра масс этого тела х2 = —√ 3 см, y2 = 0. Биссектриса сектора массы М образует угол 30° с вертикалью, так что координаты x1и у1центра масс этого сектора равны: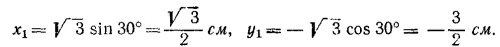
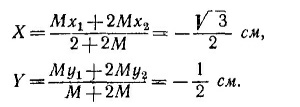
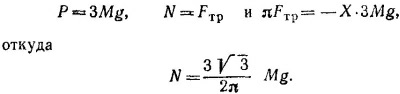
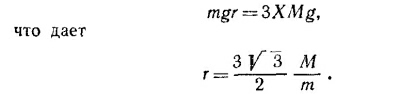
 19.16. Поскольку вся фигура, подвешенная в точке Р, находится в равновесии независимо от ее положения, точка Р является ее центром масс.
19.16. Поскольку вся фигура, подвешенная в точке Р, находится в равновесии независимо от ее положения, точка Р является ее центром масс.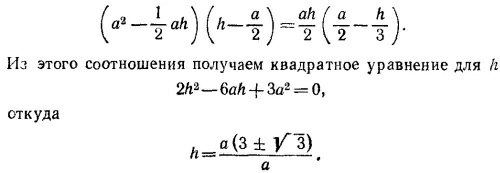
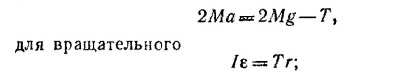
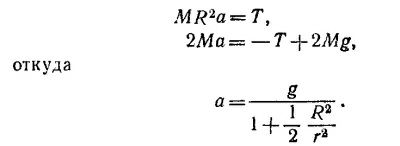
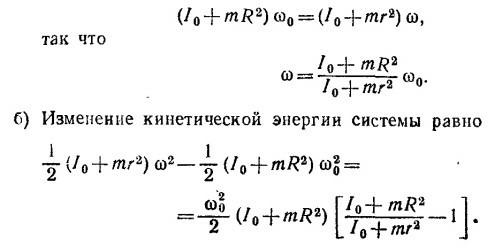
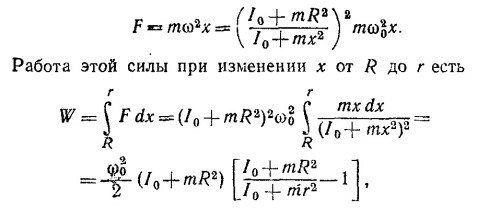
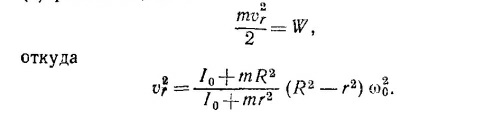

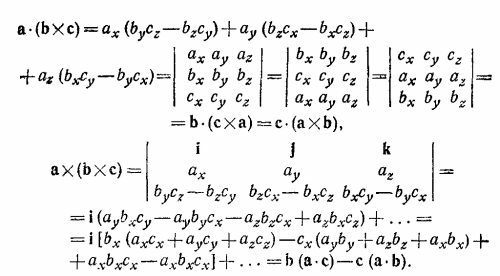
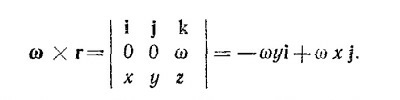

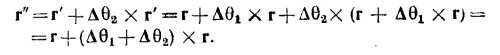
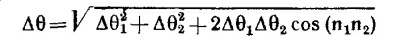
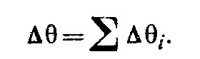
 Рассматривая угловую скорость как вектор, направленный вдоль оси вращения, модуль которого равен изменению угла в единицу времени, записываем ω¡= Δθ¡/Δt. Поэтому вращение тела с несколькими угловыми скоростями эквивалентно вращению с одной угловой скоростью
Рассматривая угловую скорость как вектор, направленный вдоль оси вращения, модуль которого равен изменению угла в единицу времени, записываем ω¡= Δθ¡/Δt. Поэтому вращение тела с несколькими угловыми скоростями эквивалентно вращению с одной угловой скоростью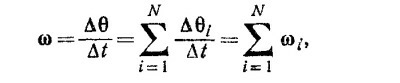
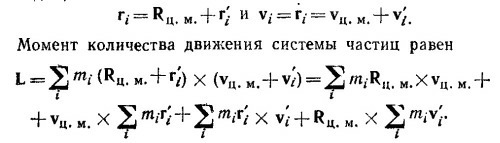
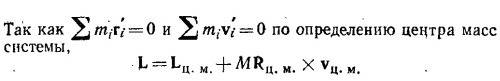
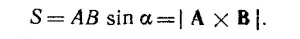
 Вектор S = A x B направлен перпендикулярно векторам А и В, т. е. его направление совпадает с нормалью к основанию.
Вектор S = A x B направлен перпендикулярно векторам А и В, т. е. его направление совпадает с нормалью к основанию.