Главная >> В мире больших скоростей >> Специальная теория относительности 8. Размеры движущегося тела
Займемся теперь проблемой измерения длины. Здесь нам также придется встретиться с некоторыми неожиданностями.
Представим себе, что нам нужно сравнить длину двух стержней. Если стержни не двигаются друг относительно друга, то сделать это несложно. Нужно только приложить их друг к другу и удостовериться, совпадают ли их концы. Сравнение движущихся отрезков осуществить сложнее.
Пусть стержни а и б параллельны и стержень б движется со скоростью v перпендикулярно самому себе (рис. 31). Для сравнения длины стержней от концов стержня а пошлем лучи света в направлении, перпендикулярном стержню. Если эти лучи попадают точно на концы стержня б, то оба стержня, следовательно, имеют одинаковую длину. Результат измерения не зависит от того, движется ли стержень б и с какой скоростью он движется.
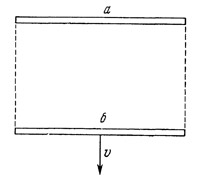 Рис. 31. Сравнение длин движущихся стержней в случае, когда стержни перпендикулярны направлению их относительного движения. Пупктирные линии изображают световой луч, направленный из конца одного стержня к концу другого Рис. 31. Сравнение длин движущихся стержней в случае, когда стержни перпендикулярны направлению их относительного движения. Пупктирные линии изображают световой луч, направленный из конца одного стержня к концу другого
В системе отсчета, связанной со стержнем а, стержни а и б равны по длине. Точно к такому же выводу придет наблюдатель, покоящийся относительно стержня б. Посланные из концов стержня б перпендикулярно ему световые лучи угодят точно в концы стержня а. И в системе стержня б стержни а и б будут иметь одинаковую длину. Мнения наблюдателей в разных инерциальных системах относительно длины стержней полностью совпадают. Это показывает, что размеры тела, перпендикулярные направлению движения, не зависят от инерциальной системы, в которой мы измеряем тело (иначе говоря, не зависят от скорости тела). Этот факт мы уже использовали раньше, когда на рис. 26 и 27 предполагали, что расстояние от часов В до зеркала не зависит от системы отсчета. А как сравнить стержни, если они параллельны и один из них движется по отношению к другому концом вперед (рис. 32), т. е. стержни все время параллельны направлению их относительного движения. Теперь сравнение стержней можно произвести только в некоторый определенный момент времени, не раньше и не позже.
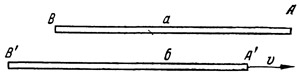 Рис. 32. Сравнение длин движущихся стержней, когда стержни параллельны направлению относительного движения. Такие стержни можно сравнивать в тот момент, когда концы А и А` совпадают Рис. 32. Сравнение длин движущихся стержней, когда стержни параллельны направлению относительного движения. Такие стержни можно сравнивать в тот момент, когда концы А и А` совпадают
Если соответствующие концы стержней а и б совпадают в один и тот же момент времени, то стержни имеют одинаковую длину. Если сначала совпадут концы А и А` и только затем концы В и В` то стержень б несомненно длиннее стержня а.
Сравнивая стержни, мы употребили понятие одновременности событий. Одновременность же зависит от системы отсчета. События, одновременные в одной инерциальной системе, не будут такими в другой. Следовательно, если оба конца стержней в некоторой инерциальной системе совпадают в один и тот же момент времени, то в других инерциальных системах это происходит в различные моменты времени.
Подчеркнем еще раз, что зависимость длины от инерциальной системы имеет место только для размеров в направлении движения. Длины, измеряемые в перпендикулярном движению направлении, не зависят от инерциальной системы.
Рассмотрим пример с поездом, о котором шла речь выше. Там наблюдатель, стоящий у насыпи, видел, что молнии у паровоза и у последнего вагона поезда сверкнули одновременно (следы молний при этом остались и на пути железной дороги), следовательно, длина поезда для наблюдателя у насыпи была равна расстоянию между следами молний. А что сказал бы об этом пассажир, находящийся в среднем вагоне поезда? По его мнению, молния у паровоза сверкнула раньше, чем у последнего вагона. Это значит, что передний конец поезда совпал со следом молнии раньше, чем задний. Следовательно, для пассажира, едущего в среднем вагоне состава, поезд будет длиннее, чем расстояние между метками молний па железнодорожном пути. Наблюдатель, стоящий у насыпи железной дороги, измерив длину движущегося поезда, получит меньшую величину, чем наблюдатель в поезде, который считает поезд покоящимся. Размеры движущегося тела меньше покоящегося. Нетрудно найти формулу, которая показывает зависимость размеров тела (в направлении движения) от скорости.
Предположим, что в описанном в § 6 опыте с часами и сигналами света наблюдатель в системе часов А измеряет расстояние между часами А и А`. Пусть оно будет равно lo. Именно настолько часы В сместились, пока сигнал света был в пути, т. е. часы В сместились на lo м за время t0 сек. Скорость часов В относительно часов А будет равна
v = lo/to (a)
Допустим, что одновременно с наблюдателем у часов А наблюдатель у часов В также измеряет расстояние между часами А и А` и пусть в результате измерения он получит 1м, т. е. длину, на которую часы А сместились за время t. Скорость часов А относительно часов В тогда будет равна
v=l/t (б)
Скорость часов В относительно часов А равна скорости часов А относительно часов В (то, что скорости направлены противоположно друг другу, нас в данном случае не интересует), поэтому мы и обозначали их одной и той же буквой v. Из равенств (а) и (б) следует:
lo/to = l/t
Умножив обе части полученного соотношения на t и подставив затем выражение г из формулы (3), получим
l = lо √ (1 - v2/c2). (4)
Таким образом, мы получили формулу, которая показывает зависимость размеров тела от скорости в направлении движения. Если длина покоящегося тела равна lо, то длина движущегося со скоростью v тела определяется формулой (4)
Чем больше скорость тела, тем короче оно по сравнению с другим точно таким же, но покоящимся телом. Не ведет ли такое следствие теории относительности к противоречиям?
Чтобы ответить на этот вопрос, рассмотрим следующий пример.
Пусть на аэродроме стоят два одинаковых самолета. Предположим далее, что один из них поднимается в воздух, делает крут над городом и с громадной скоростью проносится над самолетом, оставшимся на аэродроме. Наблюдатель, оставшийся на Земле, сравнив размеры летящего самолета с размерами самолета на аэродроме, обнаружит, что пролетевший над аэродромом самолет оказывается короче. Пусть в это же самое время размеры самолетов сравнивает также летчик в воздухе. С его точки зрения его самолет покоится, а аэродром с оставшимся на нем самолетом мчится ему навстречу. Согласно наблюдениям летчика, самолет на земле оказывается короче самолета в воздухе. Заключения наблюдателя на земле и летчика только кажутся противоречивыми. В этом кажущемся противоречии отражается закон природы: длина тела — понятие относительное. Нельзя говорить о длине тела, не указав, в какой системе отсчета эта длина измерена. Чем быстрее движется тело относительно инерциальной системы, тем короче оно в этой системе. Тело длиннее всего в той системе отсчета, где его скорость равна нулю (напомним, что речь идет все время о размерах тела в направлении движения.).
Как и все явления, предсказанные теорией относительности, сокращение тел в направлении движения незаметно при малых скоростях. Для велосипедиста, развивающего, например, скорость 18 км/час относительно шоссе, все земные предметы будут сокращаться в направлении его движения только на 0,000 000 000 000 01 %. Если смотреть с самолета, летящего со скоростью 500 км/час, предметы на поверхности земли окажутся укороченными на 0,000 000 000 01%. Это значит, что, например, расстояние между Таллином и Тарту пассажиру этого самолета будет казаться всего лишь на 1,5 стотысячных миллиметра короче, чем показывают наземные измерения. Даже скорости небесных тел слишком малы для того, чтобы можно было обнаружить сокращения, вызванные этими движениями. Солнце, например, движется относительно Земли со скоростью 30 км/сек. Обусловленное этим движением процентное сокращение диаметра Солнца в направлении движения составит 0,000 000 5%, т. е. всего-навсего 7 м. При измерении расстояния в 150 млн. км, отделяющего нас от Солнца, такая малая величина вообще несущественна.
Для скоростей, сравнимых со скоростью света, сокращение тел в направлении движения должно быть заметным. В табл. 4 представлена зависимость длины от скорости для случая, когда длина неподвижного тела равна одному метру.
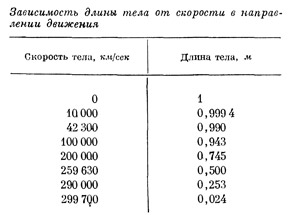
Наглядно зависимость сокращения тела в направлении движения изображена на рис. 33. На левом краю рисунка изображен стержень такой длины, которую он имеет, будучи неподвижным. Если мы хотим определить длину этого стержня, когда он движется (концом вперед) со скоростью, окажем, 100 000 км/сек, то достаточно измерить расстояние от кривой до точки на горизонтальной оси, где указано число 100 000. Это и будет соответствовать длине стержня, движущегося со скоростью 100 000 км/сек.
На рисунке видно, что, когда скорость тела приближается к скорости света, длина стержня стремится к нулю. Если бы стержень двигался точно со скоростью света, то его длина была бы равна нулю, т. е. стержень перестал бы существовать. Отсюда видно, что скорость любого тела всегда должна быть меньше скорости света. Со скоростью света могут двигаться только такие объекты, которые не имеют геометрической формы.
Таковы, например, «частицы» света — фотоны, о которых будет идти речь ниже.
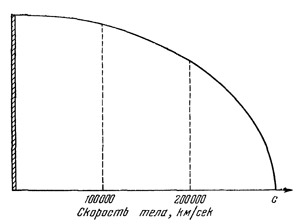 Рис. 33. Зависимость длины тела от скорости Рис. 33. Зависимость длины тела от скорости
СМОТРИТЕ ТАКЖЕ:
Социальные комментарии Cackle
|




 Рис. 31. Сравнение длин движущихся стержней в случае, когда стержни перпендикулярны направлению их относительного движения. Пупктирные линии изображают световой луч, направленный из конца одного стержня к концу другого
Рис. 31. Сравнение длин движущихся стержней в случае, когда стержни перпендикулярны направлению их относительного движения. Пупктирные линии изображают световой луч, направленный из конца одного стержня к концу другого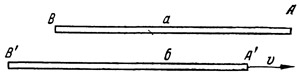 Рис. 32. Сравнение длин движущихся стержней, когда стержни параллельны направлению относительного движения. Такие стержни можно сравнивать в тот момент, когда концы А и А` совпадают
Рис. 32. Сравнение длин движущихся стержней, когда стержни параллельны направлению относительного движения. Такие стержни можно сравнивать в тот момент, когда концы А и А` совпадают
 Рис. 33. Зависимость длины тела от скорости
Рис. 33. Зависимость длины тела от скорости