Главная >> Техника быстрого счета

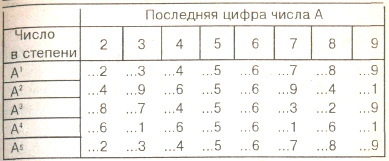
Извлечение корня высших степеней из чисел, число цифр в которых не превышает значение показателя корня

В этом случае корень определяется по последней цифре подкоренного числа.
Раз познакомившись с нижеследующей таблицей, показывающей изменение последних цифр, возведенных в различные степени чисел, вы сможете сознательно использовать данный способ, а при необходимости восстановить его технические подробности.

Таким образом последняя цифра числа, возведенного в каждую четвертую степень ( например, А¹, А⁵, А⁹ и т.д.), совпадает.

На основании этого наблюдения отметим следующее:
1) Если подкоренное число оканчивается на 5, то эта цифра и является ответом при любом остатке от деления.
Sqrt⁷ (78125) = 5.
В остальных случаях делим показатель корня на 4 и исследуем остаток от деления (функция Mod):
 
2) Mod (n,4) = 1. Если данный остаток равен 1, то последняя цифра подкоренного выражения является ответом:
Sqrt ⁹ (40353607) = 7.
 
3) Mod (n,4) = 2. Если тот же остаток равен 2, то по последней цифре находят два числа, одно из которых является ответом.
 
При последней цифре: 4 - это числа 2 или 8 (см. таблицу);
 
6 - числа 4 или 6;
9-3 или 7.

Как из пары чисел выбрать правильный ответ, будет показано ниже.

4) Mod (n,4) = 3. В этом случае искомый корень равен или последней цифре подкоренного числа, или ее дополнению до 10.
Sqrt⁷ (2187) = Sqrt¹¹(177147) = Sqrt¹⁵(14348907) = 3.

5) Mod (n,4) = 0. Подкоренное число в этом случае оканчивается на 4 или 6 (окончание на 5 мы уже рассмотрели в первом случае).

Если подкоренное число оканчивается на: 6, то искомый корень - одно из четных чисел {2, 4, 6,8}; -на 1, то это одно из нечетных чисел {1,3,7,9}.

Для окончательного определения корня пользуются:
• признаками делимости
При выборе между 4 и 6 или между 3 и 7 проверяем, делится ли число на 3 (если сумма всех цифр числа делится на 3, то да). Если делится, то корень -3 или 6, иначе 7 или 4 соответственно;

• зависимостью между числом цифр в подкоренном числе (Length) и значением показателя степени (n)
Выбор между цифрами 2-4-8 и 3-9. {Length =< n/2, то А = {2, 3};
Sqrt¹²(4096) = 2 (4< 12:2); Если {n/2 < Length =< .75*n, то А = {4};
Sqrt⁷ (16384) = 4 (7:2 < 5 < .75 * 7) {0.75*n < Length, то А = {8, 9};
Sqrt⁷ (2097152 = 8 (.75 * 7 < 7).

Примеры:
Sqrt⁷(83543). 7:4 - остаток 3. Подкоренное число оканчивается на 3, => А = 3 или 7. Число 83543 (8 + 3 + 5 + 4 + 3 = 23) на 3 не делится. Ответ: А = 7.
Sqrt⁸(65536). Mod (8,4) = 0 => А = {2, 4, 6, 8}. 83543 на 3 не делится и потому 6 исключаем. Так как .75 * 8 = 6 > Length (83543) = 5, то А = 4.

СМОТРИТЕ ТАКЖЕ: