Главная >> Фейнмановские лекции по физике >> Том 10 >> Задачи к томам I-IV 4. Кинетика. Теплота. Звук
К главе 39. Кинетическая теория газов
39.1. Можно показать, что при адиабатическом сжатии идеального газа выполняется соотношение PVγ=const [см. формулу (39.14), вып. 4, стр. 13]. С другой стороны, при всех условиях PV/T=const. Используя эти данные, найдите связь между параметрами Р и Т или V и Т для случая адиабатического сжатия.
39.2. С помощью двухтактного насоса, который используется для накачивания велосипедных шин, можно достигнуть давления 3,5 кГ/см2, начав накачку воздуха при нормальном атмосферном давлении [1 кГ/см2 при 20° С (293° К)]. Какова температура (по шкале Цельсия) воздуха, выходящего из насоса, если для воздуха γ= 1,40? Потери тепла через стенки насоса пренебрежимо малы.
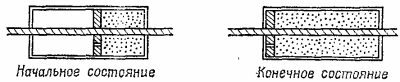 39.3. Гелий (газ) содержится в одной половине двух идентичных теплоизолированных сосудов, причем другая половина каждого из сосудов откачана до полного вакуума. Каждый сосуд разделен перегородкой, в которой имеется закрывающееся отверстие (см. рисунок). Ставятся два опыта: 39.3. Гелий (газ) содержится в одной половине двух идентичных теплоизолированных сосудов, причем другая половина каждого из сосудов откачана до полного вакуума. Каждый сосуд разделен перегородкой, в которой имеется закрывающееся отверстие (см. рисунок). Ставятся два опыта:
а) Отверстие в перегородке одного сосуда открывается, и газ перетекает в другую половину сосуда, пока не установится равновесие. Затем перегородку начинают медленно передвигать к одному из краев сосуда.
б) Перегородку другого сосуда очень медленно двигают по направлению к вакуумированному краю до упора. Сравните количественно конечное состояние газа в этих двух сосудах (трением при передвиганий перегородки можно пренебречь).
39.4. а) Представьте себе высокую вертикальную колонку, наполненную газом или жидкостью, плотность которых изменяется с высотой. Покажите, что в этом случае зависимость давления от высоты описывается дифференциальным уравнением dP/dh=–ρ(h)g.
б) Решите это уравнение для случая атмосферного воздуха (молекулярный вес μ), если его температура не зависит от высоты.
39.5. Адиабатической называется атмосфера, в которой давление и плотность в зависимости от высоты удовлетворяют соотношению Pρ–γ=const.
а) Покажите, что температура такой атмосферы линейно уменьшается с высотой, и найдите коэффициент пропорциональности. Такой температурный градиент называется адиабатическим. Найдите температурный градиент для земной атмосферы.
б) Используя аргументы, основанные на энергетических соображениях, покажите, что атмосфера с температурным градиентом, меньшим или большим адиабатического, будет соответственно стабильной или нестабильной относительно конвекции.
39.6. Цилиндр с непроницаемой абсолютно гладкой перегородкой содержит 1 м3 газа при давлении 1 атм. Газ медленно сжимается при постоянной температуре до конечного объема 0,4 м3. Какая работа затрачивается при этом?
39.7. Два газа, А и В, занимающие один и тот же начальный объем V0, при одинаковом начальном давлении Р0 внезапно подвергаются адиабатическому сжатию, каждый — до половины своего первоначального объема. Каково конечное давление в каждом газе по сравнению с начальным, если γА= 5/3 (одноатомный газ), γB = 7/5(двухатомный)?
39.8. Найти отношение количеств работы, необходимой для сжатия газов А и В, рассмотренных в задаче 39.7.
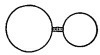 39.9. Две сферы объемом 200 и 100 см3 соединены короткой, трубкой (см. рисунок), в которой имеется изолирующая пористая перегородка. С ее помощью можно добиться равенства давлений в сосудах, но не температуры. Система находится при t=27° С и содержит кислород под давлением 760 мм рт. ст. Малая сфера помещается в сосуд со льдом при 0° С, а большая — в сосуд с паром при 100° С. Какое давление установится в системе? Тепловым расширением сфер пренебречь. 39.9. Две сферы объемом 200 и 100 см3 соединены короткой, трубкой (см. рисунок), в которой имеется изолирующая пористая перегородка. С ее помощью можно добиться равенства давлений в сосудах, но не температуры. Система находится при t=27° С и содержит кислород под давлением 760 мм рт. ст. Малая сфера помещается в сосуд со льдом при 0° С, а большая — в сосуд с паром при 100° С. Какое давление установится в системе? Тепловым расширением сфер пренебречь.
39.10.Резервуар на 50 л соединен с резервуаром на 15 л с помощью короткой трубки, в которой имеется специальный клапан давления, позволяющий газу просачиваться из большого резервуара в малый, если давление в большом превышает давление в меньшем на 88 см рт. ст. При t=17° С больший резервуар содержит газ при атмосферном давлении, а меньший — полностью вакуумирован. Каково будет давление в последнем, если оба резервуара нагреть до 162° С?
39.11.При комнатной температуре четырехокись азота частично диссоциирует в двуокись азота:
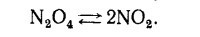 |
В вакуумированный сосуд объемом 250 см3 вводится 0,90 г жидкого N2O4 при 0° С. Когда температура в сосуде увеличивается до 27° С, жидкость испаряется, а давление становится равным 960 мм рт. ст. Сколько процентов четырехокиси азота при этом диссоциирует?
39.12. Вначале 1 моль идеального одноатомного газа находится в изолированном сосуде с подвижной крышкой, занимая объем V1 при давлении Р1 и температуре T1=27°С. Затем он медленно нагревается с помощью помещенного внутрь нагревателя, на что полностью тратится энергия 8,31 вт-ч. В результате газ расширяется при постоянном давлении Р1 нагреваясь до температуры T2 и занимая конечный объем V2. Вычислите работу, проделанную газом при расширении, и запас энергии газа, а также найдите: а) Т2, б) V2 /V1.
К главе 40. Принципы статистической механики
40.1. В радиометре молекулы газа бомбардируют тонкие легкие крылышки вертушки, которые с одной стороны зачернены, а с другой — покрыты блестящей краской. Когда на крылышки попадает излучение, поглощенная ими при этом энергия уносится в основном молекулами, бомбардирующими зачерненную сторону каждого крылышка. В результате возникает результирующая несбалансированная сила, которая поворачивает вертушку. Рассмотрим сосуд, в котором имеется n молекул массы т в единице объема, при абсолютной температуре Т. Тонкое крылышко единичной площади, расположенное внутри такого сосуда, поглощает радиационную энергию со скоростью π вт, причем эта энергия уносится (изотропно) молекулами, попадающими только на одну сторону крылышка. Оцените примерно силу, действующую на крылышко в воздухе при комнатной температуре.
40.2. Какая доля молекул газа (газ находится в тепловом равновесии), достигающих в единицу времени поверхности сосуда, обладает кинетической энергией:
а) большей, чем средняя тепловая,
б) в 3 раза большей, чем средняя тепловая?
40.3. Молярная теплоемкость вещества при постоянном объеме Cv— это количество энергии, необходимое для повышения температуры 1 моля вещества на 1°, если объем остается постоянным. Чему равна молярная теплоемкость при постоянном объеме:
а) идеального одноатомного газа?
б) идеального двухатомного газа?
40.4. Газ при нормальных давлении и температуре втекает со скоростью v через гладкую трубку с постоянным поперечным сечением площадью А. Когда газ проходит через проволочную сетку, оказывающую пренебрежимо малое сопротивление потоку, он нагревается. Приобретаемая мощность равна q вm. Из трубки газ вытекает со скоростью v′. Напишите уравнения, выражающие законы сохранения массы, энергии и импульса для случая, когда через трубку протекает воздух, а затем найдите:
а) v′,
б) конечную температуру Т,
в) напор F (основная характеристика реактивного двигателя).
40.5. Обсудите достоинства воздушного реактивного двигателя в свете предыдущей задачи, если при его работе затрачивается 100 кг воздуха и 2,00 кг керосина в секунду. Теплотворная способность керосина составляет около 4,65·107 дж/кг. Какие обстоятельства могут сделать неправильным полученный вами результат?
40.6. Закон распределения Максвелла имеет вид
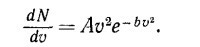 |
Он может быть преобразован так: у=х2е–x
а) Нарисуйте график этой функции для 0≤x≤3,00 и покажите, что при увеличении х главную роль играет экспоненциальный член.
б) Найдите максимальное значение у.
40.7. При атмосферном давлении закон n=n0e–mgh/kT; величина kT/mg=RT/ug определяет собой так называемую шкалу высоты (и — молекулярный вес).Рассчитайте шкалу высоты для земной атмосферы и околосолнечного пространства, если
К главе 41. Броуновское движение
41.1. Рассчитайте (и запомните):
а) температуру Т, при которой kT= 1 эв;
б) величину kT (в эв) при комнатной температуре;
в) длину волны фотона, соответствующей квантовому переходу с разностью энергий 1 эв.
41.2. Закон распределения излучения абсолютно черного тела имеет вид
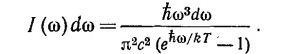 |
Перейдя к новой переменной x=hω/kT, покажите, что:
а) проинтегрированная по всем частотам полная интенсивность излучения пропорциональна четвертой степени абсолютной температуры;
б) частота ωm, при которой /(ω) имеет максимальное значение, пропорциональна абсолютной температуре.
41.3. Найдите относительные интенсивности света с длиной волны 0,31 мк, излучаемого двумя абсолютно черными телами, которые находятся при температуре 2000 и 4000° К соответственно.
К главе 42. Применения кинетической теории
42.1. Энергия активации, теплота испарения, теплоты образования или диссоциации и т. д. обычно выражаются в джоулях на 1 г-моль или в электрон-вольтах на 1 атом. Сколько дж/г-моль содержится в 1 эв/атом? (Химики обычно используют энергетическую единицу, называемую килокалорией; 1 ккал=4186 дж.)
42.2. а) Постройте график плотности паров ртути в зависимости от 1/T в полулогарифмической шкале (соответствующие данные возьмите из учебников физики и химии). С помощью графика определите теплоту испарения ртути. Сравните ваши результаты с табличной величиной,
б) Проделайте то же самое для воды.
42.3. В температурном интервале 0—300° С теплота возгонки ртути изменяется только на 3% (в средней это составляет около 0,61 эв/атом). Какую ошибку вы сделаете при расчете плотности паров ртути при 0° С, если используете теплоту возгонки при 300° С вместо правильного значения при 0° С?
Замечание. Незначительное в процентном отношении отличие в показателе экспоненты может привести к большой ошибке.
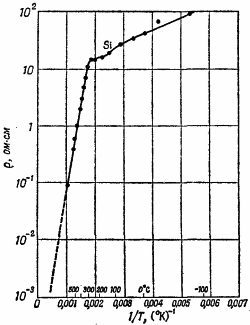 42.4. Сопротивление почти чистого кремния в зависимости от температуры показано на прилагаемом графике. Сделайте качественный вывод о природе прямого тока в этом веществе выше и ниже 300° С. 42.4. Сопротивление почти чистого кремния в зависимости от температуры показано на прилагаемом графике. Сделайте качественный вывод о природе прямого тока в этом веществе выше и ниже 300° С.
К главе 48. Диффузия
43.1. «Диаметр» молекулы кислорода приблизительно равен d=3 Å. Вычислите среднюю длину свободного пробега и среднее время между двумя столкновениями для молекул кислорода при нормальных давлении и температуре.
43.2. Сосуд содержит 1024 молекул газа, средняя длина свободного пробега одной молекулы равна l. Для какой длины пробега L вероятность того, что хоть какая-нибудь из молекул пройдет в сосуде без столкновения путь, превышающий L, меньше 50%?
43.3. Если в веществе существует температурный градиент, то происходит перенос тепла, причем количество переносимой энергии в единицу времени пропорционально этому градиенту (без учета конвекции). Коэффициент пропорциональности, приведенный к единице площади и к единице температурного градиента, называется теплопроводностью К. Таким образом, dE/dt=KA(dt/dx). Покажите, что в отсутствие конвекции теплопроводность газа равна
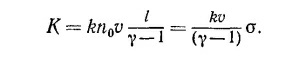 |
Примечание. Интерпретируйте теплопроводность как перенос внутренней (тепловой) энергии U через плоскость внутри вещества, как это было сделано при рассмотрении процесса диффузии.
43.4. Когда в жидкости существует градиент скорости, причем скорость зависит от расстояния в направлении, перпендикулярном потоку, то в результате возникает тормозящий движение фактор, называемый вязкостью. В газе его появление обусловлено переносом импульса. Через каждую плоскость импульс переносится молекулами, находящимися по обе стороны от нее на расстоянии, не превышающем длину свободного пробега. Если поток движется в направлении оси х и существует градиент скорости vx в направлении оси у, то сила вязкости, отнесенная к единице площади плоскости, перпендикулярной оси у, равна F/A=ηdvx/dy. Покажите, что для газа коэффициент вязкости η приближенно равен
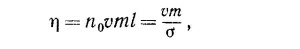 |
где n — концентрация молекул; т — масса молекулы; / — длина свободного пробега; σ=nоl.
43. 5. Отметим, что теплопроводность и вязкость газа не зависят от давления. Измените соответствующим образом формулу для количества энергии, переносимой между Двумя поверхностями, имеющими температуры Т и Т+ΔТ и находящимися на расстоянии D друг от друга, если l»D. Проделайте то же самое, рассматривая процесс переноса импульса между двумя такими поверхностями, движущимися со скоростями v и v+Δv.
43.6. Два газа А и В с плотностями ρА и ρB находятся при определенной температуре То. Отдельный ион, за которым ведется наблюдение, обладает подвижностями μA в газе А и μB в газе В (μ=vдр/F, где F — сила, см. вып. 4, стр. 90). Какова подвижность иона в смеси этих газов с плотностью ρА+ ρB при той же температуре То?
К главе 44. Законы термодинамики
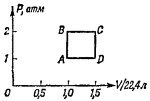 44.1. Идеальный газ, имеющий γ=4/3 последовательно переводится из состояния А (давление Р=1 атм, объем V=22,4 л, температура t=300° К) в состояние С (Р=2 атм, V=33,6 л) либо по пути ABC, либо по пути ADC. 44.1. Идеальный газ, имеющий γ=4/3 последовательно переводится из состояния А (давление Р=1 атм, объем V=22,4 л, температура t=300° К) в состояние С (Р=2 атм, V=33,6 л) либо по пути ABC, либо по пути ADC.
а) Покажите, что изменение энтропии в обоих случаях одинаково.
б) Рассчитайте это изменение.
44.2. Переведите идеальный цикл Карно abcd на диаграмме р—V между состояниями, характеризующимися параметрами Т1 и T2 и (ра, Va), (рс, Vc), в цикл ABCD на диаграмме энтропия — температура (см. фиг. 44.6 «Лекций», вып. 4, стр. 109).
44.3. Температура парогенератора на современной теплоэлектростанции, использующей перегретый пар, равна 600° С. В холодильник подается речная вода при t=20°С. Каков максимальный к. п. д., который может быть получен на такой станции?
44.4. В идеальном обратимом двигателе, в котором в качестве рабочего тела используется 28 г азота (γ=7/5). рабочий цикл abcd происходит без использования золотника (см. фиг. 44.6 «Лекций», вып. 4, стр. 109). Температура нагревателя 400° К, холодильника 300° К. Начальный объем газа в точке а равен 6,0 л, а объем в точке с составляет 18,0 л.
а) При каком объеме Vb нужно прекратить подачу в цилиндр тепла (изотермическое расширение) и, теплоизолировав его, начать адиабатическое расширение от Vb к Vc? При каком объеме Vd начнется адиабатическое сжатие?
б) Какое количество тепла поступает в систему на участке а→b цикла?
в) Какое количество тепла уходит из системы на участке c→d?
г) Чему равен к. п. д. двигателя?
д) Чему равно изменение энтропии на 1 г рабочего вещества на участках а→b и c→d?
Примечание. Вы должны получить, что для цикла Карно в случае идеального газа отношения Vb/Va и Vc/Vd равны.
44.5. Беззаботный экспериментатор, торопясь уйти, оставил золотник резервуара, наполненного гелием, неплотно закрытым. Газ, первоначально находившийся при давлении 200 атм, медленно изотермически выходит из резервуара при температуре 20° С. Чему равно изменение энтропии на 1 кг газа?
К главе 45. Примеры из термодинамики
45.1. Солнце излучает приблизительно как черное тело при температуре 5700° К. Если солнечным светом облучать абсолютно черную медную сферу, расположенную на расстоянии 1 А.Е. от Солнца, то какая равновесная температура будет достигнута при этом? (Диаметр Солнца виден с Земли под углом 0,50°.)
45.2. Солнечный свет падает перпендикулярно на некоторую область, находящуюся в Экваториальной Африке. Если поверхность излучает как абсолютно черное тело, то какова максимальная температура этой области? (Солнечная постоянная равна 1395 вт/м2.)
45.3. Черное тело радиуса r при температуре Т окружено зачерненной с обеих сторон тонкой оболочкой радиуса R. Найдите, насколько такой радиационный экран уменьшает скорость охлаждения тела. (В пространстве между телом и оболочкой — вакуум, потерь, связанных с теплопроводностью, нет.)
45.4. Плотность в центре Солнца равна приблизительно 80 г/см3, а температура ~13·106°К. Вещество Солнца почти целиком состоит из протонов и электронов. Найдите давление газа и радиационное давление в центре Солнца.
45.5. Скрытая теплота испарения воды равна приблизительно 2,44·106 дж/м3, а плотность пара при 100° С составляет 0,598 кг/м3. Используя уравнение Клаузиуса — Клапейрона, найдите скорость изменения температуры кипения с высотой в град/км, принимая за начало отсчета уровень моря. Положите температуру воздуха равной 300° К.
45.6. Покажите, что для идеального газа, внутренняя энергия которого зависит только от температуры, разность между молярными теплоемкостями при постоянном давлении и постоянном объеме равна газовой постоянной R:
Ср — Cv = R.
45.7. При 0° С удельный объем насыщенного водяного пара равен 206 м3/кг. Какова скрытая теплота испарения в дж/кг при этой температуре? (Определите dp/dt из таблиц, рассчитайте L и сравните с табличным значением.)
45.8. Тело поглощает фиксированную долю А полного излучения, падающего на его поверхность, и отражает остаток. Покажите, что при температуре Т оно излучает энергию АσТ4.
45.9. а) Используя термодинамические соображения, покажите, что если вещество при замерзании расширяется, то его температура замерзания должна уменьшаться с увеличением давления,
б) Рассчитайте самую низкую температуру льда на катке, при которой катание на коньках еще возможно.
К главе 47. Звук. Волновое уравнение
47.1. Найдите отношение скоростей звука в гелии и водороде при одной и той же температуре.
47.2. В два свистка одинаковой длины вдуваются: воздух, охлажденный почти до температуры жидкого воздуха (—180° С), и теплый воздух. Один свисток издает звук ровно на октаву выше, чем другой (т. е. удвоенной частоты). Какова должна быть температура воздуха, вдуваемого во второй свисток?
47.3. Если вы вдохнете гелий и начнете разговаривать, то звук вашего голоса будет неестественно высоким. Если все ваши резонансные полости («пустоты в вашей голове») будут заполнены гелием, а не воздухом, то насколько увеличится каждая резонансная частота? Если вы при этом напеваете, то как повлияет наличие гелия на тональность, в которой вы поете? Обсудите.
47.4. Рассмотрим постоянную плоскую звуковую волну с частотой 1000 сек–1, в которой экстремумы давления отличаются на ±1 дин/см2 от среднего атмосферного давления 1·106 дин/см2.
а) Чему равно изменение плотности, сопровождающее распространение такой волны?
б) Чему равно максимальное смещение xт частиц?
в) Чему равна интенсивность волны?
(Примите скорость звука равной 340 м/сек.)
47.5. Зажмите кончиками пальцев обеих рук резиновую полоску длиной около 5 см, а затем попросите товарища слегка щелкнуть по резине. Послышится звук. Потом растяните полоску в 2, 3, 4, 5 раз, не меняя массу полоски между руками, и повторите ту же процедуру. Обсудите результаты наблюдения. Почему ничего похожего не происходит со струной скрипки?
47.6. Однородная абсолютно гибкая струна линейной плотности σ кг/м растянута с натяжением Т. Сформулируйте волновое уравнение, описывающее поперечное смещение струны у, и найдите скорость распространения возмущения вдоль струны. Используйте предположение о том, что ду/дх«1 во всех точках в любой момент времени, и рассмотрите только плоские колебания струны. Отметим, что компонента натяжения струны в поперечном направлении очень близка к Т ду/дх.
47.7. Покажите, что выражение и=Ае¡(ωt -kx)удовлетворяет волновому уравнению
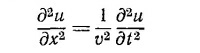 |
при условии, что ω и k связаны соотношением ω=vk
К главе 48. Биения
48.1. Фазовая скорость волны с длиной волны λ, распространяющейся по водной поверхности, если пренебречь поверхностным натяжением и конечной глубиной водоема, vфаз=√gλ/2π. Покажите, что групповая скорость волны равна половине фазовой. Чему равна групповая и фазовая скорости волны длиной 1000 м?
48.2. Если в предыдущей задаче рассматривать влияние поверхностного натяжения, то можно показать, что фазовая скорость волны на поверхности жидкости с плотностью ρ и с поверхностным натяжением T равна vфаз=(2πT/λρ+gλ/2π)1/2 когда глубина водоема достаточно велика. Найдите групповую скорость такой волны.
48.3. Найдите фазовую скорость ряби с длиной волны 1,0 см на поверхности:
а) воды (поверхностное натяжение 70 дин/см);
б) этилового спирта (поверхностное натяжение 26 дин/см).
48.4. Найдите длину волны и частоту ряби на поверхности воды, которая движется с минимальной скоростью.
48.5. Длинный дизельный товарный поезд идет в гору со скоростью 5,0 м/сек по прямому пути. Когда он достигает туннеля в отвесной скале, машинист дает длинный непрерывный гудок с основной частотой 340 гц. Звук гудка и его эхо, возникающее при отражении от стены, слышат машинист и человек, находящийся на земле вблизи последнего вагона. Какой частоты звук слышит каждый из них?
К главе 49. Собственные колебания
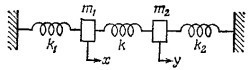 49.1. Два тела с массами т1 и m2 прикреплены к двум стенам пружинами, коэффициенты упругости которых k1 и k2 соответственно. Друг с другом они соединены пружиной с жесткостью k (см. рисунок). 49.1. Два тела с массами т1 и m2 прикреплены к двум стенам пружинами, коэффициенты упругости которых k1 и k2 соответственно. Друг с другом они соединены пружиной с жесткостью k (см. рисунок).
Напишите уравнения движения этих тел, положив
49.2. Подставьте х=Ае¡ωt и y=Be¡ωt в полученные выше уравнения и найдите частоты и отношения амплитуд грузиков для нормальных колебаний.
49.3. Покажите, что функция
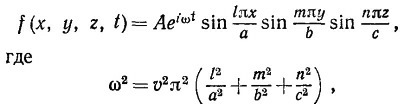 |
а /, т, n — целые числа, большие или равные единице,
а) удовлетворяет трехмерному волновому уравнению (описывающему волну со скоростью распространения v);
б) равна 0 при х=0, х=а, y=0, у=b. z=0, z=c;
в) осциллирует во времени подобно синусоиде.
49.4. Полагая, что в предыдущей задаче а : b : с=1 : 2 : 3, найдите 10 минимальных частот, выраженных через наименьшую частоту ωо. Расположите их в порядке возрастания и отложите на вертикальной шкале.
49.5. Используя понятие о бесконечно длинных периодических волнах, распространяющихся в противоположных направлениях, выясните, что произойдет, если идеальная однородная натянутая струна длины L оттянута от средней точки на расстояние А, а затем отпущена. Нарисуйте несколько положений струны в различные моменты времени в течение одного полупериода первой гармоники.
К главе 50. Гармоники
50.1. Используя фурье-разложения прямоугольной волны
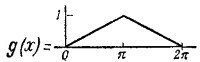
50.2. Разложите функцию
в интеграл Фурье и покажите, что полученные результаты согласуются с тем, что получается при интегрировании функции, использованной в предыдущей задаче.
50.3. Используя результат предыдущей задачи, покажите
50.4. В гл. 45 нам надо было вычислить интеграл
Теперь вы можете это сделать, умножив числитель и знаменатель на е–х, разложив подынтегральную функцию в ряд и интегрируя почленно. Получим
 Проверьте это. Проверьте это.
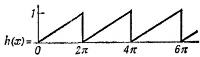
50.5. Найдите фурье-разложения пилообразной функции, которая описывает ток, протекающий в горизонтальной цепи развертки электронного осциллографа:
 50.6. Выпрямитель есть устройство, которое преобразует синусоидальную волну, например напряжения с амплитудой V0, в 50.6. Выпрямитель есть устройство, которое преобразует синусоидальную волну, например напряжения с амплитудой V0, в
а) Вычислите среднее значение V(t). Оно называется выходным напряжением.
б) Найдите амплитуду второй гармоники в выходном напряжении.
50.7. С трансформатора снимается выходное напряжение, пропорциональное Vвых=Vвх+ e(Vвх)3. Выясните, к каким эффектам приведет учет кубического члена, если:
а) входная волна синусоидальная;
б) имеются две или более входные синусоидальные волны с разными частотами.
СМОТРИТЕ ТАКЖЕ:
Социальные комментарии Cackle
|




 39.3. Гелий (газ) содержится в одной половине двух идентичных теплоизолированных сосудов, причем другая половина каждого из сосудов откачана до полного вакуума. Каждый сосуд разделен перегородкой, в которой имеется закрывающееся отверстие (см. рисунок). Ставятся два опыта:
39.3. Гелий (газ) содержится в одной половине двух идентичных теплоизолированных сосудов, причем другая половина каждого из сосудов откачана до полного вакуума. Каждый сосуд разделен перегородкой, в которой имеется закрывающееся отверстие (см. рисунок). Ставятся два опыта: 39.9. Две сферы объемом 200 и 100 см3 соединены короткой, трубкой (см. рисунок), в которой имеется изолирующая пористая перегородка. С ее помощью можно добиться равенства давлений в сосудах, но не температуры. Система находится при t=27° С и содержит кислород под давлением 760 мм рт. ст. Малая сфера помещается в сосуд со льдом при 0° С, а большая — в сосуд с паром при 100° С. Какое давление установится в системе? Тепловым расширением сфер пренебречь.
39.9. Две сферы объемом 200 и 100 см3 соединены короткой, трубкой (см. рисунок), в которой имеется изолирующая пористая перегородка. С ее помощью можно добиться равенства давлений в сосудах, но не температуры. Система находится при t=27° С и содержит кислород под давлением 760 мм рт. ст. Малая сфера помещается в сосуд со льдом при 0° С, а большая — в сосуд с паром при 100° С. Какое давление установится в системе? Тепловым расширением сфер пренебречь.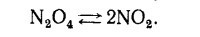
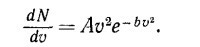
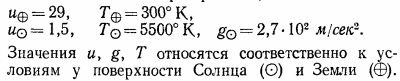
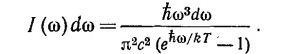
 42.4. Сопротивление почти чистого кремния в зависимости от температуры показано на прилагаемом графике. Сделайте качественный вывод о природе прямого тока в этом веществе выше и ниже 300° С.
42.4. Сопротивление почти чистого кремния в зависимости от температуры показано на прилагаемом графике. Сделайте качественный вывод о природе прямого тока в этом веществе выше и ниже 300° С.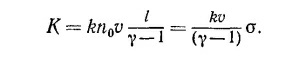
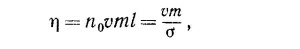
 44.1. Идеальный газ, имеющий γ=4/3 последовательно переводится из состояния А (давление Р=1 атм, объем V=22,4 л, температура t=300° К) в состояние С (Р=2 атм, V=33,6 л) либо по пути ABC, либо по пути ADC.
44.1. Идеальный газ, имеющий γ=4/3 последовательно переводится из состояния А (давление Р=1 атм, объем V=22,4 л, температура t=300° К) в состояние С (Р=2 атм, V=33,6 л) либо по пути ABC, либо по пути ADC.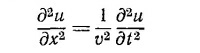
 49.1. Два тела с массами т1 и m2 прикреплены к двум стенам пружинами, коэффициенты упругости которых k1 и k2 соответственно. Друг с другом они соединены пружиной с жесткостью k (см. рисунок).
49.1. Два тела с массами т1 и m2 прикреплены к двум стенам пружинами, коэффициенты упругости которых k1 и k2 соответственно. Друг с другом они соединены пружиной с жесткостью k (см. рисунок).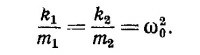
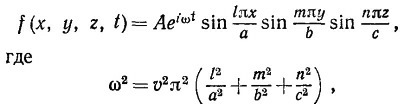

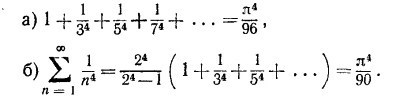
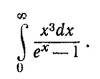
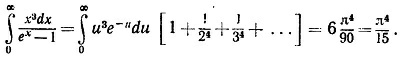
 Проверьте это.
Проверьте это. 50.6. Выпрямитель есть устройство, которое преобразует синусоидальную волну, например напряжения с амплитудой V0, в
50.6. Выпрямитель есть устройство, которое преобразует синусоидальную волну, например напряжения с амплитудой V0, в