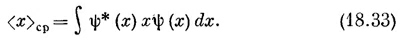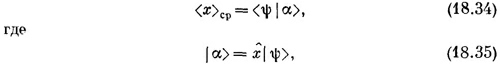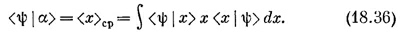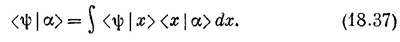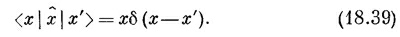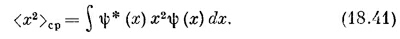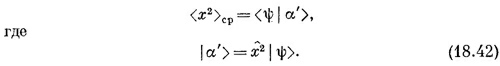| Обучение и материалы |
|---|
| Физический справочник |
| Формулы по физике |
| Шпаргалки по физике |
| Энциклопедия |
| Репетиторы по физике |
| Работа для физиков |
| Быстрый устный счет |
| Виртуальные лабораторные |
| Опыты по физике |
| ЕГЭ онлайн |
| Онлайн тестирование |
| Ученые физики |
| Необъяснимые явления |
| Ваша реклама на сайте |
| Разное |
| Контакты |
| Спецкурс |
|---|
| Фейнмановские лекции |
|
В мире больших скоростей |
Введение в теорию относительности |
|
Лекции по биофизике |
| Лекции по ядерной физике |
| Ускорение времени... |
| Лазеры |
| Нанотехнологии |
| Книги |
| полезное |
|---|
| Смешные анекдоты о физике
Готовые шпоры по физике Физика в жизни Ученые и деньги Нобелевские лауреаты Фото Видео Карта сайта |
| На заметку |
|---|
| Если вам понравился сайт, предлагаем разместить нашу кнопку |
| Дополнительно |
|---|
|
Компьютерные программы по физике 
Физика и юмор 
Онлайн тестирование по физике 
|
Оператор места
Наше уравнение для <х>ср имеет тот же вид, что (18.18). Когда мы считали среднюю энергию, мы ставили между двумя ψ оператор H, а когда считаем среднее положение, ставим просто х. (Если угодно, можете рассматривать х как алгебраический оператор «умножь на х».) Эту параллель можно провести еще дальше, выразив среднее местоположение в форме, которая соответствует уравнению (18.18). Предположим, что мы просто написали
и смотрим, не удастся ли найти такой оператор х, чтобы он создавал состояние | α>, при котором уравнение (18.34) не противоречит уравнению (18.33). Иначе говоря, мы должны найти такое | α>, чтобы было
Разложим сперва <ψ|α> по x-представлению:
Сравним затем интегралы в (18.36) и (18.37). Вы видите, что в х-представлении (и только в этом представлении)
Воздействие на |ψ> оператора х для получения |α> равнозначно умножению ψ (х)=<х|ψ> на х для получения α (х) =<х|α>. Перед нами определение оператора х в координатном представлении.
Тогда вы сможете доказать поразительную формулу
т. е. что оператор х обладает интересным свойством: когда он действует на базисное состояние | х>, то это равнозначно умножению на х.)
Или, если желаете, можно написать и так:
Под х2 подразумевается хх — два оператора применяются друг за другом. С помощью (18.42) можно подсчитать <x2>ср, пользуясь каким угодно представлением (базисными состояниями). Если вам нужно знать среднее значение хn или любого многочлена по х, то вы легко это теперь проделаете. СМОТРИТЕ ТАКЖЕ:Социальные комментарии Cackle |
© All-Физика, 2009-2025
При использовании материалов сайта ссылка на www.all-fizika.com обязательна.
При использовании материалов сайта ссылка на www.all-fizika.com обязательна.

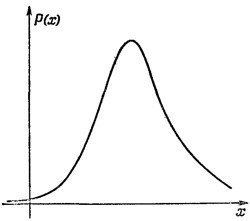 Каково среднее местоположение электрона в атоме? В данном состоянии |ψ> каково среднее значение координаты х? Разберем одномерный случай, а обобщение на трехмерный или на системы с большим числом частиц останется на вашу долю. Мы имеем состояние, описываемое функцией ψ (x), и продолжаем раз за разом измерять х. Что получится в среднем? Очевидно, ∫хР (х) dx, где Р(х)—вероятность обнаружить электрон в небольшом элементе длины dx возле х. Пусть плотность вероятности Р(х) меняется с х так, как показано на фиг. 18.1. Вероятнее всего вы обнаружите электрон где-то возле вершины кривой. Среднее значение х тоже придется куда-то на область невдалеке от вершины, а точнее, как раз на центр тяжести площади, ограниченной кривой.
Каково среднее местоположение электрона в атоме? В данном состоянии |ψ> каково среднее значение координаты х? Разберем одномерный случай, а обобщение на трехмерный или на системы с большим числом частиц останется на вашу долю. Мы имеем состояние, описываемое функцией ψ (x), и продолжаем раз за разом измерять х. Что получится в среднем? Очевидно, ∫хР (х) dx, где Р(х)—вероятность обнаружить электрон в небольшом элементе длины dx возле х. Пусть плотность вероятности Р(х) меняется с х так, как показано на фиг. 18.1. Вероятнее всего вы обнаружите электрон где-то возле вершины кривой. Среднее значение х тоже придется куда-то на область невдалеке от вершины, а точнее, как раз на центр тяжести площади, ограниченной кривой.