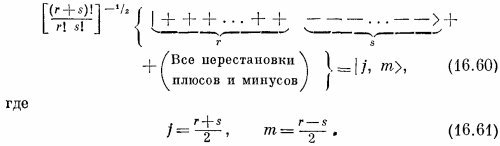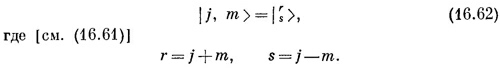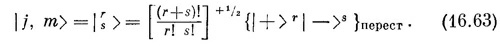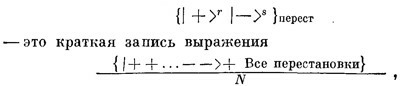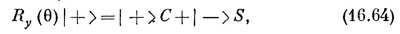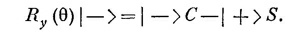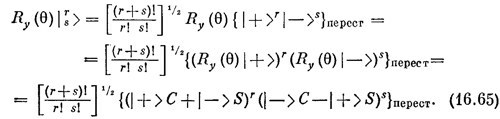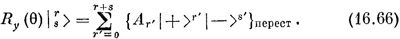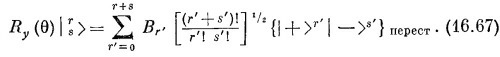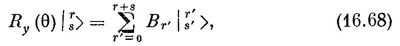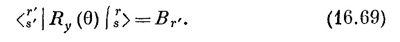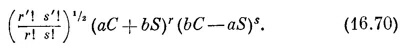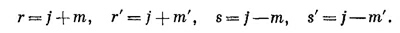Главная >> Фейнмановские лекции по физике >> Том 9 >> Глава 16. Момент количества движения

Добавление 1. Вывод матрицы поворота

Для тех, кто хотел бы разобраться в этом поподробнее, мы вычислим сейчас общую матрицу поворота для системы со спином (полным моментом количества движения) j. В расчете общего случая на самом деле большой необходимости нет; важно понять идею, а все результаты вы сможете найти в таблицах, которые приводятся во многих книжках. Но, с другой стороны, вы зашли уже так далеко, что у вас, естественно, может возникнуть желание убедиться, что вы и впрямь в состоянии понять даже столь сложные формулы квантовой механики, как (16.35).
 
Расширим рассуждения § 4 на систему со спином j, которую будем считать составленной из 2j объектов со спином ¹/₂. Состояние с m=j имело бы вид | + + +...+> (с j плюсами). Для m=j — 1 было бы 2j членов типа | + + . . . + + —>, | + + . . . + — + > и т. д. Рассмотрим общий случай, когда имеется r плюсов и s минусов, причем r+s=2j. При повороте вокруг оси z от каждого из r плюсов появится множитель е+^¡φ/2. В итоге фаза изменится на i (r/2 — s/2) φ. Мы видим, что

Как и в случае J=³/₂, каждое состояние с определенным т должно быть суммой всех состояний с одними и теми же r и s, взятых со знаком плюс, т. е. состояний, отвечающих всевозможным перестановкам с r  плюсами и s минусами. Мы считаем, что вам известно, что всего таких сочетаний есть (r+s)!/r!s!. Чтобы нормировать каждое состояние, надо эту сумму разделить на корень квадратный из этого числа. Можно написать

Введём еще новые обозначения, они нам помогут в счете. Ну а поскольку мы уж определили состояния при помощи (16.60), то два числа r и s определяют состояние ничуть не хуже, чем j и т. Мы легче проследим за выкладками, если обозначим

Далее, (16.60) мы запишем, пользуясь специальным обозначением

Обратите внимание, что показатель степени в общем множителе мы изменили на +¹/₂. Это оттого, что внутри фигурных скобок в (16.60) стоит как раз N=(r+s)!/r!s! слагаемых. Если сопоставить (16.63) с (16.60), то ясно, что

где N — количество различных слагаемых в скобках. Эти обозначения удобны тем, что каждый раз при повороте все знаки плюс вносят один и тот же множитель, так что в итоге он получается в r-й степени. Точно так же все знаки минус дадут некоторый множитель в s-й степени, в каком бы порядке эти знаки ни стояли.
 
Теперь положим, что мы повернули нашу систему вокруг оси у на угол θ. Нас интересует R (θ) | ^r_s>. Оператор R (θ), действуя на каждый | + >, дает

где  С = cos θ/2 и S = sin θ/2.  Когда  же R (θ) действует  на | —>, это приводит к

Так что искомое выражение равно

Теперь надо возвысить биномы в степень и перемножить. Появятся члены со всеми степенями |+> от нуля до r+s. Посмотрим, какие члены дадут r′-ю степень |+>. Они всегда будут сопровождаться множителем типа |—>^s′, где s′=2j— r′. Соберем их вместе. Получится сумма членов типа |+>^r′ | —>^s′ с численными коэффициентами А_r′, куда входят коэффициенты биномиального разложения вместе с множителями С и S. Уравнение (16.65) тогда будет выглядеть так:

Теперь разделим каждое А_r′ на множитель [(r′+s′)!/r′!s′!]^1/₂ и обозначим частное через В_r′. Тогда (16.66) превратится в

[Можно просто сказать, что требование, чтобы (16.67) совпадало с (16.65), определяет В_r′]
 
Если так определить В_r′, то оставшиеся множители в правой части (16.67) будут как раз состояниями  |^T′_S′>.   Итак, имеем

где s′ всегда равняется r+s — r′. А это, конечно, означает, что коэффициенты В_r′ и есть искомые матричные элементы

Теперь, чтобы найти  В_r′,  остается  немного: лишь пробиться через алгебру.
 
Сравнивая (16.67) с (16.65) и вспоминая, что r′+s′ = r+s, мы видим, что В_r′ — это просто коэффициент при a^r′b^s′ в выражении

Осталась лишь нудная работа разложить скобки по биному Ньютона и собрать члены с данными степенями а и b. Если вы все это проделаете, то увидите, что коэффициент при a^r′b^s′ в (16.70) имеет вид

Сумма берется по всем целым k, при которых аргументы факториалов больше или в крайнем случае равны нулю. Это выражение и есть искомый матричный элемент.
 
В конце надо вернуться к нашим первоначальным обозначениям j, т и т′, пользуясь формулами

Проделав эти подстановки, получим уравнение (16.34) из § 4.

СМОТРИТЕ ТАКЖЕ: