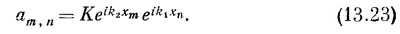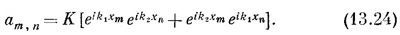Главная >> Фейнмановские лекции по физике >> Том 9 >> Глава 13. Приближение независимых частиц

Независимые частицы

В предыдущем параграфе мы написали гамильтониан (13.15) для двухчастичной системы. Затем, пользуясь приближением, эквивалентным пренебрежению каким-либо «взаимодействием» между двумя частицами, мы нашли стационарные состояния, описываемые формулами (13.17) и (13.18). Это состояние попросту есть произведение двух одночастичных состояний. Но решение, которое мы написали для а_т,n [формула (13.18)], на самом деле удовлетворить нас не может. Мы с самого начала подчеркивали, что состояние | х₉, x₄> не отличается от состояния |x₄, x₉>,что порядок х_т и х_n неважен. Вообще говоря, алгебраическое выражение для амплитуды С_т,_п не должно меняться от перестановки значений х_т и х_n, потому что она не изменяет состояния. В любом случае она будет представлять амплитуду того, что спин, направленный вниз, обнаружится в х_т и в х_n. Но обратите внимание, что (13.18) несимметрично по х_т и х_n, поскольку k₁ и k₂, вообще говоря, различны.
 
Все дело в том, что мы не заставили наше решение (13.15) подчиниться этому добавочному условию. К счастью, пока нетрудно все исправить. Заметьте, во-первых, что ничуть не хуже формулы (13.18) другое решение уравнения Гамильтона:

И даже энергия здесь та же самая, что была в (13.18). Значит, любая линейная комбинация (13.18) и (13.23) также будет решением системы и будет обладать по-прежнему энергией, даваемой (13.19). Решение, которое нужно выбрать по требованиям симметрии,— просто сумма (13.18) и (13.23):

Теперь при данных k₁ и к₂ амплитуда С_m,n не зависит от того, в каком порядке мы берем х_т и х_n; если мы случайно поставим х_т и х_n в обратном порядке, мы получим ту же амплитуду. И наше толкование уравнения (13.24) на языке «магнонов» тоже станет иным. Уже нельзя говорить, что уравнение представляет одну частицу с волновым числом k₁ и другую частицу с волновым числом k₂. Амплитуда (13.24) представляет одно состояние с двумя частицами (магнонами). Состояние характеризуется двумя волновыми числами k₁ и k₂. Наше решение выглядит как составное состояние одной частицы с импульсом р₁ = k₁/h и другой частицы с импульсом р₂ = k₂/h, но в этом состоянии нельзя сказать, где какая частица.
 
В этот момент полезно вспомнить гл. 2 (вып. 8) и наш рассказ о тождественных частицах. Мы просто только что показали, что частицы спиновых волн (магноны) ведут себя как тождественные бозе-частицы. Все амплитуды обязаны быть симметричны по координатам двух частиц; это все равно, что сказать, что после «обмена двумя частицами» мы снова получим ту же амплитуду с тем же знаком. Но вы можете подумать: «Почему же мы все-таки решили в (13.24) сложить два члена? Почему не вычесть?» Ведь при знаке минус обмен х_т и х_n просто изменил бы знак а_т,n, а это не в счет, это не имеет значения. Но ведь обмен х_т с х_n ничего не меняет — все электроны кристалла останутся там же, где и были, так что даже для перемены знака нет, казалось бы, никакого повода. Но это, конечно, плохой аргумент.
 
Наше обсуждение имело двойную цель: во-первых, рассказать вам кое-что о спиновых волнах; во-вторых, продемонстрировать состояние, амплитуда которого равна произведению двух амплитуд, а энергия равна сумме энергий, отвечающих этим амплитудам. Для независимых частиц амплитуда получается умножением, а энергия — сложением. Почему сложением — легко понять. Энергия — это коэффициент при t в мнимом показателе экспоненты; она пропорциональна частоте. Если пара объектов что-то совершает, один с амплитудой e^–iE₂t/h, а другой с амплитудой e^–iE₁t/h , и если амплитуда того, что обе эти вещи произойдут вместе, является произведением отдельных амплитуд, то в произведении появится единственная частота, равная сумме двух частот. Энергия, отвечающая произведению амплитуд, есть сумма обеих энергий.
 
Нам понадобилось довольно долго говорить, чтобы сообщить очень простую вещь: когда вы не учитываете взаимодействия между частицами, вы вправе рассматривать каждую частицу независимо. Они могут отдельно существовать во всевозможных состояниях, в которых они пребывали бы и порознь, и давать тот же вклад в энергию, какой давали бы порознь. Однако следует помнить, что если частицы тождественны, то они могут вести себя как бозе- или ферми-частицы в зависимости от задачи. Например, пара электронов, добавленная к Кристаллу, ведет себя как ферми-частицы. Обмен местоположениями двух электронов приводит к перемене знака амплитуды. В уравнении, соответствующем (13.24), между двумя слагаемыми стоит знак минус. Как следствие этого: две ферми-частицы не могут пребывать в точности в одних и тех же условиях — с одинаковыми спинами и одинаковыми k. Амплитуда такого состояния нуль.

СМОТРИТЕ ТАКЖЕ: