| Обучение и материалы |
|---|
| Физический справочник |
| Формулы по физике |
| Шпаргалки по физике |
| Энциклопедия |
| Репетиторы по физике |
| Работа для физиков |
| Быстрый устный счет |
| Виртуальные лабораторные |
| Опыты по физике |
| ЕГЭ онлайн |
| Онлайн тестирование |
| Ученые физики |
| Необъяснимые явления |
| Ваша реклама на сайте |
| Разное |
| Контакты |
| Спецкурс |
|---|
| Фейнмановские лекции |
|
В мире больших скоростей |
Введение в теорию относительности |
|
Лекции по биофизике |
| Лекции по ядерной физике |
| Ускорение времени... |
| Лазеры |
| Нанотехнологии |
| Книги |
| полезное |
|---|
| Смешные анекдоты о физике
Готовые шпоры по физике Физика в жизни Ученые и деньги Нобелевские лауреаты Фото Видео Карта сайта |
| На заметку |
|---|
| Если вам понравился сайт, предлагаем разместить нашу кнопку |
| Дополнительно |
|---|
|
Компьютерные программы по физике 
Физика и юмор 
Онлайн тестирование по физике 
|
Уровни энергии
Теперь мы готовы к тому, чтобы вычислить уровни энергии основного состояния водорода, решая гамильтоновы уравнения (10.14). Мы хотим найти энергии стационарных состояний. Это значит, что мы должны отыскать те особые состояния | ψ>, для которых каждая из принадлежащих | ψ> амплитуд C¡= <i| ψ> обладает одной и той же зависимостью от времени, а именно е–¡ωt. Тогда состояние будет обладать энергией Е=hω. Значит, мы ищем совокупность амплитуд, для которых
где четверка коэффициентов ai не зависит от времени. Чтобы увидеть, можем ли мы получить эти амплитуды, подставим (10.17) в (10.14) и посмотрим, что из этого выйдет. Каждое ihdC¡/dt в (10.14) перейдет в ЕС¡. И после сокращения на общий экспоненциальный множитель каждое С¡ превратится в а¡; получим
Это и нужно решить для отыскания а1, а2, а3 и a4. Право, очень мило со стороны первого уравнения, что оно не зависит от остальных,— а это значит, что одно решение сразу видно. Если выбрать Е=А, то
даст решение. (Конечно, если принять все а равными нулю, то это тоже будет решение, но состояния оно не даст!) Будем считать наше первое решение состоянием | />:
Его энергия
Все это немедленно дает ключ ко второму решению, получаемому из последнего уравнения в (10.18):
Это решение мы назовем состоянием |//>:
Дальше пойдет чуть труднее; оставшиеся два уравнения (10.18) переплетены одно с другим. Но мы все это уже делали. Сложив их, получим
Окидывая это взглядом и припоминая знакомый нам уже аммиак, мы видим, что здесь есть два решения:
Это смеси состояний |2> и |3>. Обозначая их |///> и |/V> и вставляя для правильной нормировки множитель 1/√2, имеем
Ошибка составляет только три стомиллиардных! Вероятно, ни одна из фундаментальных физических величин не измерена лучше, чем эта; таково одно из наиболее выдающихся по точности измерений в физике. Теоретики были очень счастливы, когда им удалось вычислить энергию с точностью до 3·10–5;но к этому времени она была измерена с точностью до 2·10–11,т.е. в миллион раз точнее, чем в теории. Так что экспериментаторы идут далеко впереди теоретиков. В теории основного состояния атома водорода и вы, и мы находимся в одинаковом положении. Вы ведь тоже можете взять значение А из опыта — и всякому, в конце концов, приходится делать то же самое. СМОТРИТЕ ТАКЖЕ:Социальные комментарии Cackle |
При использовании материалов сайта ссылка на www.all-fizika.com обязательна.


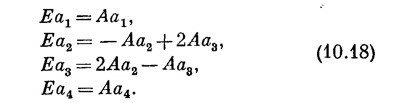
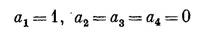
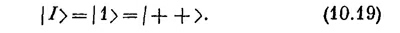
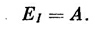
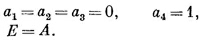
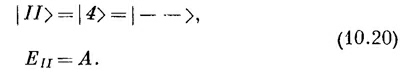
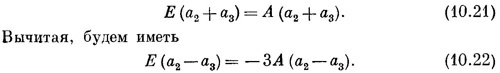
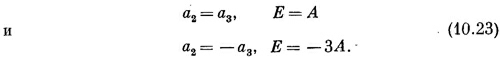
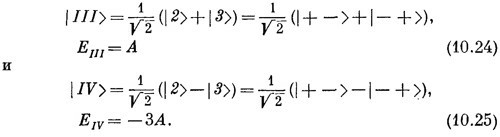
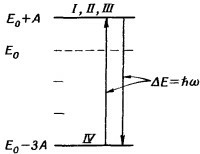 Мы нашли четверку стационарных состояний и их энергии. Заметьте, кстати, что наши четыре состояния ортогональны друг другу, так что их тоже можно при желании считать базисными состояниями. Задача наша полностью решена.
Мы нашли четверку стационарных состояний и их энергии. Заметьте, кстати, что наши четыре состояния ортогональны друг другу, так что их тоже можно при желании считать базисными состояниями. Задача наша полностью решена.