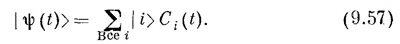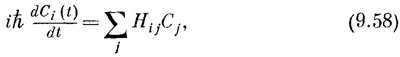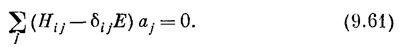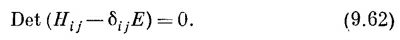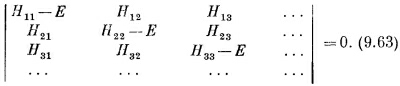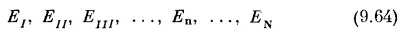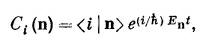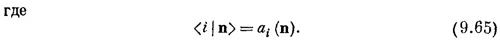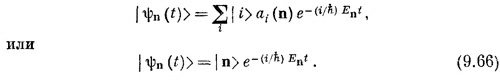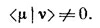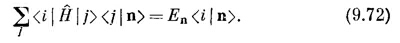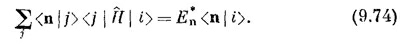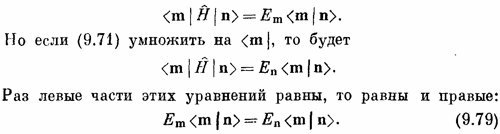Главная >> Фейнмановские лекции по физике >> Том 8 >> Глава 9. Еще системы с двумя состояниями

Обобщение на системы с N состояниями

Мы покончили с системами с двумя состояниями, рассказав все, что хотелось. В дальнейших главах мы перейдем к изучению систем с большим числом состояний. Расширение на системы с N состояниями идей, разработанных для двух состояний, проходит довольно просто. Это делается примерно так.
 
Если система обладает N различными состояниями, то всякое состояние |ψ (t) > можно представить как линейную комбинацию произвольной совокупности базисных состояний | ¡>, где ¡=1, 2, 3, . . ., N:

Коэффициенты  C_¡(t) — это амплитуды  < i | ψ (t)>.  Поведение амплитуд С_¡ во времени направляется уравнениями

где энергетическая матрица H_¡j описывает физику задачи. С виду она такая же, как и для двух состояний. Но только теперь и i, и j должны пробегать по всем N базисным состояниям, и энергетическая матрица H_¡j (или, если вам больше нравится, гамильтониан) — это теперь матрица NxN, состоящая из N² чисел. Как и прежде, H_¡j=H_j¡ (до тех пор, пока частицы сохраняются) и диагональные элементы H_¡¡ суть вещественные числа.
 
Мы нашли общее решение для всех С в системе с двумя состояниями, когда энергетическая матрица постоянна (не зависит от t). Точно так же нетрудно решить и уравнение (9.58) для системы с N состояниями, когда Н не зависит от времени. Опять мы начинаем с того, что ищем возможное решение, в котором у всех амплитуд зависимость от времени одинакова. Мы пробуем

Если все эти С_¡ подставить в (9.58), то производные dC_¡ (t)/dt превращаются просто в (— i/h) EC_¡ Сокращая повсюду на общую экспоненту, получаем

Эта система N линейных алгебраических уравнений для N неизвестных а_1; а₂, . . ., а_n; решение у нее бывает только тогда, когда вам сильно повезет, когда определитель из коэффициентов при всех а равен нулю. Но не нужно чересчур умничать: можете просто начать их решать любым способом, и вы сразу увидите, что решить их удается лишь при некоторых значениях Е. (Вспомните, что единственная величина, которая в этих уравнениях подлежит подгонке,  это Е.)
 
Если, впрочем, вы хотите, чтобы все было по форме, перепишите (9.60) так:

Затем примените правило (если оно вам знакомо), что эти уравнения будут иметь решения лишь для тех значений Е, для которых

Каждый член в детерминанте — это просто H_ij и только из диагональных отнято Е. Иначе говоря, (9.62) означает просто

Это, конечно, всего-навсего особый способ записывать алгебраические уравнения для Е, складывая вереницы членов, перемножаемых в определенном порядке. Эти произведения дадут все степени Е вплоть до E^N.
 
Значит, у нас есть многочлен N-й степени, который равняется нулю. У него, вообще говоря, есть N корней. (Нужно помнить, однако, что некоторые из них могут быть кратными корнями; это значит, что два или более корней могут быть равны друг другу.) Обозначим эти N корней так:

(пусть n обозначает n-е порядковое числительное, так что n принимает значения /,//, . . ., N). Некоторые из этих энергий могут быть между собой равны, скажем Е_II=Е_III, но мы решили все же обозначать их разными именами.
 
Уравнения (9.60) или (9.61) имеют по одному решению для каждого значения Е [из (9.64)]. Если вы подставите любое из Е, скажем E_n в (9.60) и найдете все а_¡, то получится ряд чисел а_¡, относящихся к энергии Е_n . Этот ряд мы обозначим а_¡ (n).
 
Если подставить эти а_¡ (n) в (9.59), то получатся амплитуды C_¡ (n) того, что состояния с определенной энергией находятся в базисном состоянии | i>. Пусть |n> обозначает вектор состояния для состояния с определенной энергией при t=0. Тогда можно написать

Полное состояние с определенной энергией   | ψ_n (t) >  можно тогда записать так:

Векторы состояний | n> описывают конфигурацию состояний с определенной энергией, но с вынесенной зависимостью от времени. Это постоянные векторы, которые, если мы захотим, можно использовать в качестве новой базисной совокупности.
 
Каждое из состояний |n> обладает тем свойством (в чем легко убедиться), что при действии на него оператором Гамильтона H получится просто Е_n , умноженное на то же состояние:

Значит, энергия Е_n — это характеристическое число оператора Гамильтона Н. Как мы видели, у гамильтониана в общем случае бывает несколько характеристических энергий. Физики обычно называют их «собственными значениями» матрицы Н. Для каждого собственного значения Н, иными словами, для каждой энергии, существует состояние с определенной энергией, которое мы называли «стационарным». Состояния | n> обычно именуются «собственными состояниями Н», Каждое собственное состояние отвечает определенному собственному значению Е_n.
 
Далее, состояния | n> (их N штук) могут, вообще говоря, тоже быть выбраны в качестве базиса. Для этого все состояния должны быть ортогональны в том смысле, что для любой пары их, скажем | n> и | m>,

Это выполнится автоматически, если все энергии различны. Кроме того, можно умножить все а_¡ (n) на подходящие множители, чтобы все состояния были отнормированы: чтобы для всех n было

Когда оказывается, что (9.63) случайно имеет два (или больше) одинаковых корня с одной и той же энергией, то появляются небольшие усложнения. По-прежнему имеются две различные совокупности a_¡,  отвечающие двум одинаковым энергиям,  но состояния, которые они дают, не обязательно ортогональны. Пусть вы проделали нормальную процедуру и нашли два стационарных состояния с равными энергиями. Обозначим их |μ> и | v >. Тогда они не обязательно окажутся ортогональными: если вам не повезло, то обнаружите, что

Но зато всегда верно, что можно изготовить два новых состояния (обозначим их | μ′ > и | v′> с теми же энергиями, но ортогональных друг другу:

Этого можно добиться, составив | μ′> и |v′> из подходящих линейных комбинаций | μ > и | v > с так подобранными коэффициентами, что (9.70) будет выполнено. Это всегда полезно делать, и мы будем вообще предполагать, что это уже проделано, так что можно будет считать наши собственноэнергетические состояния |n> все ортогональными.
 
Для интереса докажем, что когда два стационарных состояния обладают разными энергиями, то они действительно ортогональны. Для состояния | n> с энергией Е_n

Это операторное уравнение на самом деле означает, что имеется соотношение между числами. Если заполнить недостающие части, то оно означает то же самое, что и

Проделав здесь комплексное сопряжение, получим

Теперь вспомним, что комплексно сопряженная амплитуда — это амплитуда обратного процесса, так что (9.73) можно переписать в виде

Поскольку это уравнение справедливо для всякого i, то его можно «сократить» до

Это уравнение называется сопряженным с (9.71).
 
Теперь легко доказать, что Е_n — число вещественное. Умножим (9.71) на <n|. Получится

(с учетом, что  = 1). Умножим теперь (9.75) справа на |n> :

Сравнивая (9.76) с (9.77), видим, что

а это означает, что Е_n вещественно. Звездочку при Е_n в (9.75) можно убрать.
 
Теперь наконец-то мы в силах доказать, что состояния с различными энергиями ортогональны. Пусть | т> и I m> — пара базисных состояний с определенными энергиями. Написав (9.75) для состояния | m> и умножив его на | n>, получим

Если Е_т = Е_n, то это равенство ни о чем не говорит. Но если энергии двух состояний | m> и | n> различны (Е_т≠Е_n), то уравнение (9.79) говорит, что <m | n> должно быть нулем, что мы и хотели доказать. Два состояния обязательно ортогональны, если только Е_n и Е_т отличаются друг от друга.

СМОТРИТЕ ТАКЖЕ: