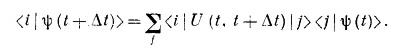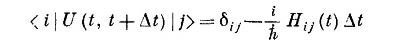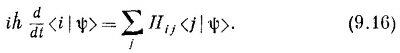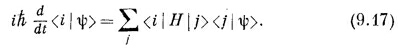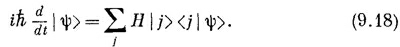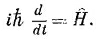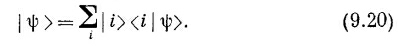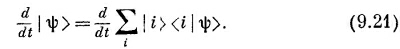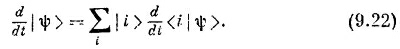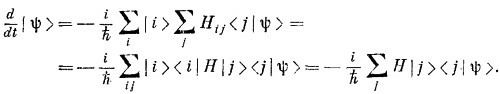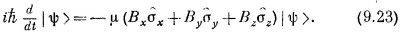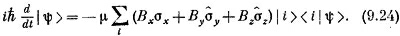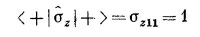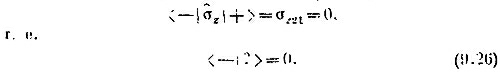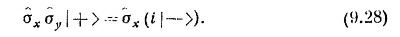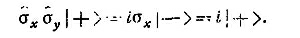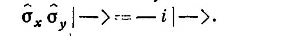Главная >> Фейнмановские лекции по физике >> Том 8 >> Глава 9. Еще системы с двумя состояниями

Спиновые матрицы как операторы

Раз уж мы занялись математическими обозначениями, то хотелось бы описать еще один способ записи, способ, часто употребляемый из-за своей краткости. Он прямо следует из обозначений, введенных в гл. 6. Если имеется система в состоянии | ψ (t) >. изменяющемся во времени, то можно, как мы это делали в уравнении (6.31), написать амплитуду того, что система при t + Δt оказалась бы в состоянии | ¡>:

Матричный элемент <¡|U (t, t+Δt) |j>— это амплитуда того, что базисное состояние |j> превратится в базисное состояние | i > за время Δt. Затем мы определяли Н_¡j при  помощи

и показывали, что амплитуды  С_¡(t) = <¡ | ψ (t)> связаны дифференциальными уравнениями

Если амплитуды С_¡ записать явно, то это же уравнение будет выглядеть  по-иному:

Далее, матричные элементы H_¡j — это тоже амплитуды, которые можно записывать в виде < i | Н | j>; наше дифференциальное уравнение выглядит тогда так:

Мы видим, что —¡/h <i |H| j> — это амплитуда того, что в физических условиях, описываемых матрицей Н, состояние | j> за время dt «генерирует» состояние | ¡> (Все это неявно подразумевалось в рассуждениях гл. 6, § 4.)
 
Теперь, следуя идеям гл. 6, § 2, мы можем сократить в (9.17) общий «множитель» < i |, поскольку (9.17) справедливо при любом | ¡>, и записать это уравнение просто в виде

Или, сделав еще один шаг, убрать к тому же и j и написать

В гл. 6 мы указывали, что при такой записи Н в Н | j> или  в Н | ψ> называется оператором. Отныне на операторы мы будем надевать маленькие шапочки (ˆ), чтобы напоминать вам, что это оператор, а не число. Мы будем писать Н^ˆ | ψ>. Хотя оба уравнения (9.18) и (9.19) означают в точности то же самое, что и (9.15) или (9.17), мы можем думать о них совершенно иначе. Haпримep, уравнение (9.18) можно было бы описывать так: «Производная по времени от сектора состояния |ψ> равняется тому, что получается от действия оператора Гамильтона Hˆ на каждое базисное состояние, умноженному на амплитуду <j | ψ> того, что ψ окажется в состоянии j, и просуммированному по всем j». Или уравнение (9.19) можно описать так: «Производная по времени (умноженная на ih) от состояния | ψ> равняется тому, что вы получите, если подействуете гамильтонианом Нˆ на вектор состояния |ψ>». Это просто сокращенный способ выражения того, что содержится в (9.17), но, как вы потом убедитесь, он может оказаться очень удобным.
 
Если хотите, идею «абстрагирования» можно продвинуть еще на шаг. Уравнение (9.19) справедливо для всякого состояния |ψ>. Кроме того, левая сторона ihd/dt — это тоже оператор; его действие: «продифференцируй по t и умножь на ih». Итак, (9.19) можно рассматривать как уравнение между операторами — операторное уравнение

Оператор Гамильтона (с точностью до константы), действуя на любое состояние, приводит к тому же результату, что и d/dt. Помните, что это уравнение, как и (9.19), не есть утверждение о том, что оператор Нˆ просто та же операция, что и d/dt. Эти уравнения — динамический закон природы (закон движения) для квантовой системы.
 
Только для того, чтобы попрактиковаться в этих представлениях, продемонстрирует вам другой вывод уравнения (9.18). Вы знаете, что любое состояние | ψ> можно записать через его проекции на какой-то базис [см. (6.8)]:

Как же меняется |ψ > во времени? Продифференцируем его:

Но базисные состояния | i > во времени не меняются (по крайней мере у нас они всегда были определенными, закрепленными состояниями), и только амплитуды <¡| ψ> — это числа, которые могут меняться. Иначе говоря, (9.21) превращается в

Во ведь d< i |ψ >/dt нам известно—это (9.16); получается, следовательно,

А это опять-таки уравнение (9,18).
 
Итак, на гамильтониан можно смотреть по-разному. Можно рассматривать совокупность коэффициентов Н_¡j просто как компанию чисел, можно говорить об «амплитудах» < i | Н | j>, можно представлять себе «матрицу» Н_¡j и можно считать его «оператором» Hˆ. Все это одно и то же.
 
Вернемся теперь к нашей системе с двумя состояниями. Если уж мы записываем гамильтониан через матрицы сигма (с подходящими численными множителями, такими, как В_х и т. д.), то естественно рассматривать и σ^x_¡j как амплитуду < i | σ_х | j>, или, для краткости, как оператор σ_х. Если применить эту идею оператора, то уравнение движения состояния |ψ> в магнитном поле можно написать в виде

Желая «использовать» это уравнение, нам, естественно, приходится выражать |ψ> через базисные векторы (равносильно тому, что приходится находить компоненты пространственных векторов, когда задача доводится до числа). Так что обычно мы предпочитаем расписывать (9.23) в более раскрытом виде:

Сейчас вы увидите, чем красива идея оператора.Чтобы применять уравнение (9.24), нужно знать, что будет, когда операторы σˆ подействуют на каждое базисное состояние. Напишем σˆ_z | +>; это какой-то вектор | ?>, но какой? Что ж, умножим его слева на <+ | и получим

(пользуясь табл.  9.1). Итак,  мы знаем, что

Теперь умножим   σ_z |+> слева на < — |.  Получится

Существует только  один вектор состояния,  удовлетворяющий в  (9.25)  и  (9.2U);  это  I+->.  Мы. стало быть,  открыли,   что

Такого poда рассуждениями можно легко  показать, что все свойства матриц сигма могут быть в операторных обозначениях описаны рядом правил, приведенных в табл.9.3.

Если у нас есть произведения матриц сигма, то они переходят в произведения операторов. Когда два оператора стоят рядом в виде произведения, то сперва приступает к операции тот оператор, который стоит правее. Скажем, под σ_xσ_y|+> надо понимать σ_х (σ_y |+>).  Из табл.  9.3 получаем σ_y |+> = ¡ | – >, так   что

Числа (как. например, ¡) просто проходят сквозь операторы (операторы действуют только на векторы состояний);значит, 14,28) перейдет в

Если сделать то же самое с σ_х σ_y| —>. то получится

Если взглянуть на табл. 9.3, то видно, что σ_хσ_y, действуя на |+> или | —>, даст в точности  то же, что получается, если просто подействовать оператором σ_z и умножить на — ¡. Поэтому можно сказать, что операция σ_хσ_y совпадает с операцией iσ_z, и записать это утверждение в виде операторного уравнения

Убедитесь, что это уравнение совпадает с одним из наших матричных уравнений табл. 9.2. Итак, мы опять видим соответствие между матричной и операторной точкой зрения. Каждое из уравнений в табл. 9.2 может поэтому рассматриваться и как уравнение относительно операторов сигма. Можно проверить, что они действительно следуют из табл. 9.3. Работая с этими вещами, лучше не следить за тем, являются ли величины типа σ или Н операторам, или матрицами. Чем их ни считай, уравнения выйдут одни и те же, так что табл. 9.2 можно при желании относить то к операторам сигма, то к матрицам сигма.

СМОТРИТЕ ТАКЖЕ: