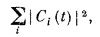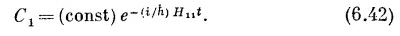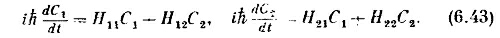Главная >> Фейнмановские лекции по физике >> Том 8 >> Глава 6. Гамильтонова матрица

Гамильтонова матрица

Идея, стало быть, заключается в том, что для квантовомеханического описания мира нужно выбрать совокупность базисных состояний i и написать физические законы, задавая матрицу коэффициентов H_ij Тогда у нас будет все, что нужно,— мы сможем отвечать на любой вопрос о том, что случится. Нам остается выучить правила, по которым находят H в соответствии с данной физической обстановкой: какое Н отвечает магнитному полю, какое электрическому и т. д. Это самая трудная часть дела. К примеру, для новых странных частиц мы совершенно не представляем, какие H_ij употреблять. Иными словами, никто не знает полного H_ij для всего мира. (Частично трудность заключается в том, что едва ли можно надеяться на открытие H_ij, раз никому не известно, каковы базисные состояния!) Мы действительно владеем превосходными приближениями для нерелятивистских явлений и некоторых других особых случаев. В частности, мы знаем вид H_ij, требуемый для движений электронов в атомах — для описания химии. Но мы не знаем полного, истинного H для всей Вселенной.
 
Коэффициенты H_ij называют гамилътоновой матрицей, или, короче, просто гамильтонианом. (Как получилось, что Гамильтон, работавший в 30-х годах прошлого века, дал свое имя квантовомеханической матрице,—история длинная.) Много лучше было бы называть ее энергетической матрицей по причинам, которые станут ясны, когда мы поработаем с ней. Итак, все сошлось на гамильтониане. Как узнать гамильтониан — вот в чем вопрос!
 
У гамильтониана есть одно свойство, которое выводится сразу же:

Это следует из того, что полная вероятность пребывания системы хоть в каком-то состоянии не должна меняться. Если вначале у вас была частица (или любой объект, или весь мир), то с течением времени она пропасть не может. Полная вероятность ее  где-то найти равна

что не должно меняться со временем. Если это обязано выполняться для любого начального условия φ, то уравнение (6.40) тоже должно соблюдаться.
 
В качестве первого примера возьмем случай, когда физические условия не меняются со временем; мы имеем в виду внеиише физические условия, так что Н не зависит от времени, никаких магнитов никто не включает и не выключает. Выберем также систему, для описапия которой хватает одного базисного состояния; такое приближение годится для покоящегося атома водорода и сходных систем. Уравнение (6.39) тогда утверждает, что

Только одно уравнение — и все! Если Н₁₁ постоянно, это дифференциальное уравнение легко  решается,  давая

Так зависит от времени состояние с определенной энергией Е=Н₁₁. Вы видите, почему H_¡j следовало бы называть энергетической матрицей: она обобщает понятие энергии на более сложные случаи.
 
Вслед  за  этим, чтобы еще  лучше  разобраться  в смысле уравнений, рассмотрим систему с двумя базисными состояниями. Тогда  (6.39)  читается так:

Если все Н опять не зависят от времени, то эти уравнения легко решить. Для интереса займитесь этим сами, а мы позже еще вернемся к ним. Вот вы уже и можете вести расчеты по квантовой механике, зная об Н только то, что оно не зависит от времени!

СМОТРИТЕ ТАКЖЕ: