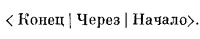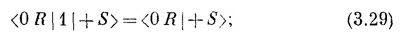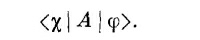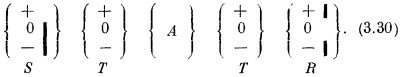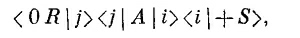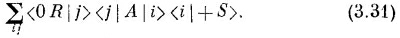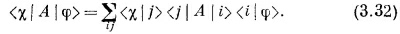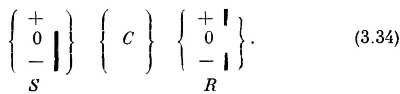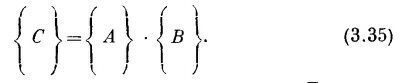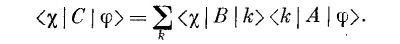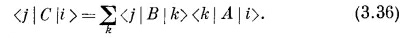| Обучение и материалы |
|---|
| Физический справочник |
| Формулы по физике |
| Шпаргалки по физике |
| Энциклопедия |
| Репетиторы по физике |
| Работа для физиков |
| Быстрый устный счет |
| Виртуальные лабораторные |
| Опыты по физике |
| ЕГЭ онлайн |
| Онлайн тестирование |
| Ученые физики |
| Необъяснимые явления |
| Ваша реклама на сайте |
| Разное |
| Контакты |
| Спецкурс |
|---|
| Фейнмановские лекции |
|
В мире больших скоростей |
Введение в теорию относительности |
|
Лекции по биофизике |
| Лекции по ядерной физике |
| Ускорение времени... |
| Лазеры |
| Нанотехнологии |
| Книги |
| полезное |
|---|
| Смешные анекдоты о физике
Готовые шпоры по физике Физика в жизни Ученые и деньги Нобелевские лауреаты Фото Видео Карта сайта |
| На заметку |
|---|
| Если вам понравился сайт, предлагаем разместить нашу кнопку |
| Дополнительно |
|---|
|
Компьютерные программы по физике 
Физика и юмор 
Онлайн тестирование по физике 
|
Механика квантовой механики
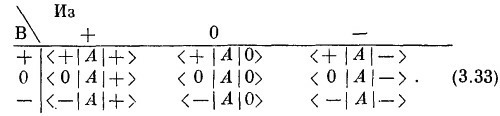
Мы покажем вам сейчас, почему полезны эти законы. Пусть у нас есть атом в заданном состоянии (под этим мы подразумеваем, что он как-то был приготовлен), и мы хотим знать, что с ним будет в таком-то опыте. Иными словами, мы начинаем с состояния φ атома и хотим знать, каковы шансы, что он пройдет через прибор, который пропускает атомы только в состоянии x. Законы говорят, что мы можем полностью описать прибор тремя комплексными числами <x | i > — амплитудами того, что каждое из базисных состояний окажется в состоянии x, и что мы, пустив атом в прибор, можем предсказать, что произойдет, если опишем состояние атома, задав три числа < i | φ>,— амплитуды того, что атом из своего первоначального состояния перейдет в любое из трех базисных состояний. Это очень и очень важная идея. Рассмотрим другую иллюстрацию. Подумаем о следующей задаче. Начинаем с прибора S, затем имеется какая-то сложная мешанина, которую мы обозначаем A, а дальше стоит прибор R:
Под А мы подразумеваем любое сложное расположение приборов Штерна — Герлаха — с перегородками и полуперегородками, под всевозможными углами, с необычными электрическими и магнитными полями,— словом, годится все, что вам придет в голову. (Очень приятно ставить мысленные эксперименты — тогда нас не тревожат никакие заботы, возникающие при реальном сооружении приборов!) Задача состоит в следующем: с какой амплитудой частица, входящая в область А в состоянии (+ S), выйдет из него в состоянии (0 R), так что сможет пройти через последний фильтр R? Имеется стандартное обозначение для такой амплитуды:
Как обычно, это надо читать справа налево:
Если случайно окажется, это А ничего не меняет, а просто является открытым каналом, тогда мы пишем
эти два символа равнозначны. В более общих задачах мы можем заменить (+ S) общим начальным состоянием φ, а (0 R) — общим конечным состоянием x и захотеть узнать амплитуду
Полный анализ прибора А должен был бы дать нам амплитуду <x | А | φ > для каждой мыслимой пары состояний φ и x — бесконечное количество комбинаций! Как же сможем мы тогда дать краткое описание поведения прибора А? Это можно сделать следующим путем. Вообразим, что мы видоизменили прибор (3.28) так:
На самом деле это вовсе не видоизменение, потому что широко раскрытые приборы Т ничего нигде не меняют. Но они подсказывают нам, как проанализировать проблему. Имеется определенная совокупность амплитуд <¡ | +S> того, что атомы из S перейдут в состояние i прибора Т. Затем имеется другая совокупность амплитуд того, что состояние i (по отношению к Т), войдя в А, выйдет оттуда в виде состояния j (по отношению к Т). И наконец, имеется амплитуда того, что каждое состояние j пройдет через последний фильтр в виде состояния (0 R). Для каждого допустимого пути существует амплитуда вида
и полная амплитуда есть сумма членов, которые можно получить из всех сочетаний ¡ и j. Нужная нам амплитуда равна
Если (0 R) и (+S) заменить общими состояниями x и φ, то получится выражение такого же рода; так что общий результат выглядит так:
Теперь заметьте, что правая часть (3.32) на самом деле «проще» левой части. Прибор А полностью описан девятью числами < j |A| ¡ >, сообщающими, каков отклик А на три базисных состояния прибора Т. Как только мы узнаем эту девятку чисел, мы сможем управиться с любой парой входных и выходных состояний φ и x, если только определим каждое из них через три амплитуды перехода в каждое из трех базисных состояний (или выхода из них). Результат опыта предсказывается с помощью уравнения (3.32).
Вся математика квантовой механики является простым расширением этой идеи. Приведем несложный пример. Пусть имеется прибор С, который мы хотим проанализировать, т. е. рассчитать различные < j |C| i >. Скажем, мы хотим знать, что случится в эксперименте типа
Но затем мы замечаем, что С просто состоит из двух частей, стоящих друг за другом приборов А и В. Сперва частицы проходят через А, а потом — через В, т. е. можно символически записать
Мы можем прибор С назвать «произведением» А и В. Допустим также, что мы уже знаем, как эти две части анализировать; таким образом, мы можем узнать матрицы А и В (по отношению к Т). Тогда наша задача решена. Мы легко найдем <x | С | φ> для любых входных и выходных состояний. Сперва мы напишем
Понимаете, почему? (Подсказка: представьте, что между A и В поставлен прибор T.) Если мы затем рассмотрим особый случай, когда φ и x также базисные состояния (прибора Т), скажем ¡ и j, то получим
Это уравнение дает нам матрицу прибора «произведения» С через матрицы приборов А и В. Математики именуют новую матрицу < j | С I ¡ >. образованную из двух матриц < j | В | ¡ > и < j | А | ¡ > в соответствии с правилом, указанным в (3.36), матричным «произведением» В А двух матриц В и А. (Заметьте, что порядок существен, АВ ≠ ВА.) Итак, можно сказать, что матрица для стоящих друг за другом двух частей прибора — это матричное произведение матриц для этих двух приборов порознь (причем первый прибор стоит в произведении справа). И каждый, кто знает матричную алгебру, поймет, что речь идет просто об уравнении (3.36). СМОТРИТЕ ТАКЖЕ:Социальные комментарии Cackle |
При использовании материалов сайта ссылка на www.all-fizika.com обязательна.