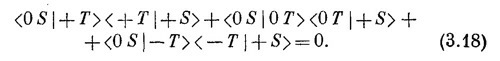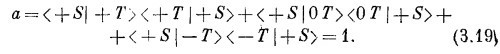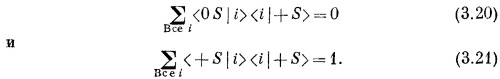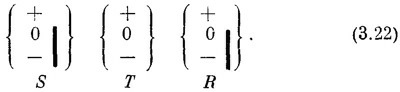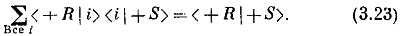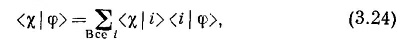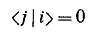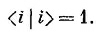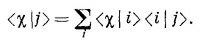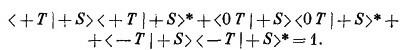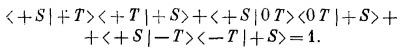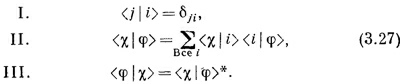| Обучение и материалы |
|---|
| Физический справочник |
| Формулы по физике |
| Шпаргалки по физике |
| Энциклопедия |
| Репетиторы по физике |
| Работа для физиков |
| Быстрый устный счет |
| Виртуальные лабораторные |
| Опыты по физике |
| ЕГЭ онлайн |
| Онлайн тестирование |
| Ученые физики |
| Необъяснимые явления |
| Ваша реклама на сайте |
| Разное |
| Контакты |
| Спецкурс |
|---|
| Фейнмановские лекции |
|
В мире больших скоростей |
Введение в теорию относительности |
|
Лекции по биофизике |
| Лекции по ядерной физике |
| Ускорение времени... |
| Лазеры |
| Нанотехнологии |
| Книги |
| полезное |
|---|
| Смешные анекдоты о физике
Готовые шпоры по физике Физика в жизни Ученые и деньги Нобелевские лауреаты Фото Видео Карта сайта |
| На заметку |
|---|
| Если вам понравился сайт, предлагаем разместить нашу кнопку |
| Дополнительно |
|---|
|
Компьютерные программы по физике 
Физика и юмор 
Онлайн тестирование по физике 
|
Интерферирующие амплитуды
Как же это может быть, что, когда переходят от (3.15) к (3.17), т. е. когда открывается больше каналов, через фильтры начинает проходить меньше атомов? Это и есть старый, глубокий секрет квантовой механики — интерференция амплитуд. С такого рода парадоксом мы впервые встретились в интерференционном опыте, когда электроны проходили через две щели. Помните, мы тогда увидели, что временами кое-где получается меньше электронов, когда обе щели открыты, чем когда открыта одна. Численно это получается вот как. Можно написать амплитуду того, что атом пройдет в приборе (3.17) через Т и S′ в виде суммы трех амплитуд — по одной для каждого из трех пучков в Т; эта сумма равна нулю:
Ни одна из трех отдельных амплитуд не равна нулю: например, квадрат модуля второй амплитуды есть γα [см. (3.15)`], но их сумма есть нуль. Тот же ответ получился бы, если бы мы настроили S′ на то, чтобы отбирать состояние (— S). Однако при расположении (3.16) ответ уже другой. Если обозначить амплитуду прохождения через Т и S′ буквой а, то в этом случае мы будем иметь
В опыте (3.16) пучок сперва расщеплялся, а потом восстанавливался. Как мы видим, Шалтая-Болтая удалось собрать обратно. Информация о первоначальном состоянии (+ S) сохранилась — все выглядит так, как если бы прибора Т вовсе не было. И это будет верно, что бы ни поставили за «до отказа раскрытым» прибором Т. Можно поставить за ним фильтр R — под каким-нибудь необычным углом — или что-угодно. Ответ будет всегда одинаков, как будто атомы шли в S′ прямо из первого фильтра S.
Точно так же в опыте, в котором S′ заменяется совершенно произвольным фильтром R, мы имеем
Результаты будут всегда такими же, как если бы прибор Т убрали и осталось бы только
Или на математическом языке
Это и есть наш основной закон, и он справедлив всегда, если только i обозначает три базисных состояния любого фильтра.
где i должно пробегать по всем трем базисным состояниям некоторого определенного фильтра.
для любых неравных между собой i и j. Конечно, мы знаем, что
Эти два уравнения обычно пишут так:
где δ¡j- («символ Кронекера») — символ, равный по определению нулю при i ≠ j и единице при i = j.
Но (3.25) утверждает, что <i | j> равно нулю, если только i не равно j, так что сумма обращается просто в <x | j> и получается тождество, что говорит о том, что эти два закона не независимы.
Если теперь посмотреть на (3.24) и предположить, что и φ, и x — это состояние ( + S), то слева получится <+S | + S>, а это, конечно, равно единице, и мы должны получить (3.19)
Эти два уравнения согласуются друг с другом (для всех относительных ориентации приборов Т и S) только тогда, когда
Стало быть, для любых состояний φ и x
Если бы этого не было, вероятности «не сохранились бы» и частицы «терялись бы».
В этих уравнениях i и j относятся ко всем базисным состояниям какого-то одного представления, тогда как φ и x — это любое возможное состояние атома. Важно отметить, что закон II справедлив лишь тогда, когда суммирование проводится по всем базисным состояниям системы (в нашем случае по трем: + Т, 0 T, — Т). Эти законы ничего не говорят о том, что следует избирать в качестве базиса. Мы начали с прибора Т, который является опытом Штерна — Герлаха с какой-то произвольной ориентацией, но и всякая другая ориентация, скажем W, тоже подошла бы. Вместо i и j нам пришлось бы ставить другую совокупность базисных состояний, но все законы остались бы правильными; какой-то единственной совокупности не существует. Успех в квантовой механике часто определяется тем, умеете ли вы использовать тот факт, помня, что расчет можно вести из-за этого разными путями. СМОТРИТЕ ТАКЖЕ:Социальные комментарии Cackle |
При использовании материалов сайта ссылка на www.all-fizika.com обязательна.