| Обучение и материалы |
|---|
| Физический справочник |
| Формулы по физике |
| Шпаргалки по физике |
| Энциклопедия |
| Репетиторы по физике |
| Работа для физиков |
| Быстрый устный счет |
| Виртуальные лабораторные |
| Опыты по физике |
| ЕГЭ онлайн |
| Онлайн тестирование |
| Ученые физики |
| Необъяснимые явления |
| Ваша реклама на сайте |
| Разное |
| Контакты |
| Спецкурс |
|---|
| Фейнмановские лекции |
|
В мире больших скоростей |
Введение в теорию относительности |
|
Лекции по биофизике |
| Лекции по ядерной физике |
| Ускорение времени... |
| Лазеры |
| Нанотехнологии |
| Книги |
| полезное |
|---|
| Смешные анекдоты о физике
Готовые шпоры по физике Физика в жизни Ученые и деньги Нобелевские лауреаты Фото Видео Карта сайта |
| На заметку |
|---|
| Если вам понравился сайт, предлагаем разместить нашу кнопку |
| Дополнительно |
|---|
|
Компьютерные программы по физике 
Физика и юмор 
Онлайн тестирование по физике 
|
Суперпозиция решений
Перейдем теперь к другой интересной проблеме. Предположим, что нам задана какая-нибудь внешняя сила Fa(например, периодическая сила с частотой ω=ωα, но наши выводы будут верны для любой зависимости силы от времени) и мы нашли движение, соответствующее этой силе (переходные движения можно учитывать или не учитывать, это неважно). Предположим, что мы решили еще одну задачу — нашли движение в случае действия силы Fb. После этого предположим, что кто-то вбежал в комнату и сказал: «На контрольной задают задачу с силой Fa+Fb. Что нам делать?» Конечно, мы решим эту задачу — ведь мы сразу обнаружим одно замечательное свойство: сумма решений ха и хb, получаемых в том случае, если брать силы по отдельности, будет решением новой задачи. Для этого надо только вспомнить о (25.3):
Еще один пример принципа суперпозиции. В гл. 12 (вып. 1) говорилось об одном из важнейших фактов, вытекающих из законов электричества. Если нам задано распределение зарядов qa, можно найти электрическое поле Еа, порождаемое этими зарядами в точке Р. Другое распределение зарядов qb порождает в этой же точке поле Еb. Оба эти распределения, действуя вместе, породят в точке Р поле Е, которое представляет собой сумму полей Еа и Еb. Иначе говоря, поле, соответствующее совокупности многих зарядов,— это векторная сумма полей, соответствующих отдельным зарядам. Аналогия с предыдущим примером бросается в глаза: ведь если мы знаем результат действия отдельных сил, то отклик на силу, являющуюся суммой этих сил, будет суммой отдельных откликов.
Причина справедливости принципа суперпозиции в электричестве состоит в том, что основные законы электричества, определяющие электрическое поле (уравнения Максвелла), — это линейные дифференциальные уравнения, обладающие свойством (25.3). Силам в этих уравнениях соответствуют заряды, порождающие электрическое поле, а уравнения, определяющие электрическое поле по заданным зарядам,— линейные уравнения. Чтобы придумать еще один пример принципа суперпозиции, спросите себя, как вам удается настроить свой радиоприемник на определенную радиостанцию, хотя одновременно работает очень много станций. Сигналы радиостанций — это колеблющиеся электрические поля очень высокой частоты, действующие на антенну радиоприемника. Амплитуда этих колебаний, правда, меняется, их модулирует голос диктора, но скорость этих изменений очень мала и об этом можно пока забыть. Когда вы слышите: «Станция работает на частоте 780 килогерц», это значит, что частота излучаемого антенной радиостанции электромагнитного поля равна 780 000 колебаний в секунду и это поле с точно такой же частотой раскачивает электроны в антенне вашего приемника. Но ведь в то же самое время поблизости может работать и другая радиостанция на другой частоте, скажем на частоте 550 кгц. Эта станция тоже раскачивает электроны вашей антенны. Как же отделяются сигналы, поступающие в приемник с частотой 780 кгц, от сигналов, имеющих частоту 550 кгц? Ведь вы же не слышали голоса обоих дикторов одновременно.
Несколько слов о механизме настройки. Как мы настраиваем радиоприемник? Мы изменяли частоту ω0, меняя L или С цепи, потому что частота цепи зависит от комбинации L и С. Большинство радиоприемников устроено так, что в них меняется значение С. Поворачивая ручку настройки приемника, мы изменяем собственную частоту цепи. Пусть какому-то положению ручки соответствует частота ωс; если нет радиостанций, работающих на этой частоте, приемник молчит. Вы продолжаете изменять емкость С цепи, пока не построите кривую отклика с резонансом при частоте ωb, тогда вы услышите другую станцию. Вот так и настраивается радиоприемник; все дело в принципе суперпозиции, в сочетании с резонансным откликом. Чтоб закончить обсуждение, давайте подумаем, как поступить при анализе линейных задач с заданной силой, когда сила очень сложно зависит от времени. Можно поступать по-разному, но есть два особенно удобных общих метода решения таких задач. Первый метод: предположим, что мы можем решить задачу в некоторых частных случаях, например в случае синусоидальных сил разных частот. Решать линейные уравнения в таких случаях — детская забава. Пусть нам и встретился этот «детский» случай. Теперь встает вопрос, нельзя ли представить любую силу в виде суммы двух или более «детских» сил? Мы уже показали на фиг. 25.1 довольно хитрую зависимость силы от времени; если туда добавить еще несколько синусоид, то результирующая кривая будет выглядеть еще сложнее. Таким образом, простенькие «детские» силы могут породить очень сложную силу. Верно и обратное: практически каждая кривая может быть представлена в виде бесконечной суммы синусоидальных волн разной длины волн (или частоты). Таким образом, мы знаем, как представить заданную силу F в виде синусоидальных волн, поэтому решение х можно представить в виде суммы F синусоидальных волн, каждая из которых умножается на эффективное отношение х к F. Такой метод решения называют методом преобразования Фурье, или анализом (разложением) Фурье. Мы не будем сейчас делать такого разложения; пока достаточно только идеи.
Такую силу можно представить в виде последовательных ударов молотком. Сначала всюду стоит тишина, потом кто-то берет в руки молоток и внезапно раздаются равномерные удары — удар, удар, удар, удар, ... и опять все тихо. Иначе говоря, непрерывно действующую силу можно представить в виде ряда последовательных импульсов, быстро следующих один за другим. Мы знаем последствия одного импульса, а последствием серии импульсов будет ряд затухающих колебаний; нарисуйте кривую колебаний для первого импульса, затем, немного отступя, такие же кривые для второго импульса, третьего и т. д. Потом сложите все кривые. Таким образом математически можно представить полное решение в случае произвольной силы, если можно решить задачу для импульса. Ответ для любой силы можно получить путем интегрирования. Это метод функции Грина. Функция Грина — это отклик системы на отдельный импульс, а метод функции Грина — это метод анализа действия силы суммированием откликов на импульсы. Физические принципы, лежащие в основе обоих методов, очень просты; они просто напрашиваются, если понять смысл линейного уравнения, но математические методы содержат довольно сложные интегрирования и т. д.; мы мало подготовлены, чтобы прямо атаковать эти методы. К этому вы еще вернетесь, когда поднабьете руку в математике. Но сама идея методов, право, очень проста. Наконец, скажем еще, почему линейные системы так важны. Ответ прост: потому что мы умеем решать линейные уравнения! Поэтому большую часть времени мы будем решать линейные задачи. Вторая (и главная) причина заключается в том, что основные законы физики часто линейны. Например, уравнения Максвелла для законов электромагнетизма — линейные уравнения. Великие законы квантовой механики, насколько нам они известны, тоже сводятся к линейным уравнениям. Вот почему мы так много времени уделяем линейным уравнениям: если мы поняли линейные уравнения, мы готовы в принципе понимать очень многие вещи. Упомянем еще другие ситуации, когда возникают линейные уравнения. Когда отклонения малы, многие функции можно приближенно заменить линейными. Например, точное уравнение движения маятника гласит
Это уравнение решается при помощи эллиптических функций, но легче его решить численно, как мы это делали в гл. 9 (вып. 1) при изучении ньютоновых законов движения. Большинство нелинейных уравнений вообще можно решить лишь численно. Для малых углов sin θ практически равен θ, и в этом случае можно перейти к линейному уравнению. На этом примере можно сообразить, что есть много обстоятельств, при которых малые эффекты линейны (здесь эго отклонения маятника на малые углы). Другой пример: если на пружине качается небольшой грузик, сила пропорциональна растяжению пружины. Если сильно потянуть за пружину, она может и порваться, значит, в этом случае сила совсем иначе зависит от расстояния! Линейные уравнения очень важны. Они настолько важны, что физики и инженеры, пожалуй, половину своего времени тратят на решение линейных уравнений. СМОТРИТЕ ТАКЖЕ:Социальные комментарии Cackle |
При использовании материалов сайта ссылка на www.all-fizika.com обязательна.

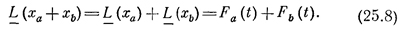
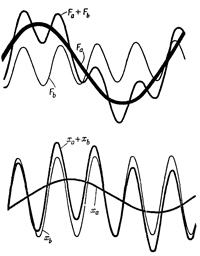 Это пример того, что называют принципом суперпозиции для линейных систем, и это очень важная вещь. Дело обстоит так: если мы сможем представить сложную силу в виде суммы нескольких более простых сил и сможем решить уравнение для каждой силы в отдельности, то мы сможем решить и первоначальное уравнение, потому что для этого надо просто объединить куски решения так же, как мы объединяли отдельные силы, чтобы получить полную силу (фиг. 25.1).
Это пример того, что называют принципом суперпозиции для линейных систем, и это очень важная вещь. Дело обстоит так: если мы сможем представить сложную силу в виде суммы нескольких более простых сил и сможем решить уравнение для каждой силы в отдельности, то мы сможем решить и первоначальное уравнение, потому что для этого надо просто объединить куски решения так же, как мы объединяли отдельные силы, чтобы получить полную силу (фиг. 25.1).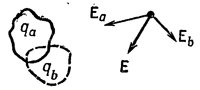
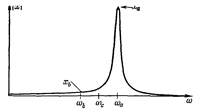 Первая часть электрической цепи радиоприемника — это линейная цепь. По принципу суперпозиции ее отклик на электрическое поле Fa+Fb равен ха+хb. По всему выходит, что нам придется слушать обоих дикторов сразу. Но вспомним, что в резонансной цепи кривая отклика х на единичную силу F зависит от частоты примерно так, как это изображено на фиг. 25.3. В цепи с очень большим значением Q отклик имеет очень острый максимум. Предположим, что обе станции имеют примерно одинаковую мощность, поэтому обе силы имеют примерно одинаковую амплитуду. Отклик равен сумме откликов ха и хb, но на фиг. 25.3 ха громаден, а хb очень мал. Таким образом, хотя оба сигнала одинаковы по силе, в приемнике они проходят через остро резонансную цепь, настроенную на частоту ωа (частоту передач одной из станций), и отклик на эту частоту (станцию) значительно больше отклика на все остальные. Поэтому, несмотря на то что на антенну действуют оба сигнала, полный отклик почти целиком составлен из частоты ωа, и мы можем выбрать ту станцию, какую пожелаем.
Первая часть электрической цепи радиоприемника — это линейная цепь. По принципу суперпозиции ее отклик на электрическое поле Fa+Fb равен ха+хb. По всему выходит, что нам придется слушать обоих дикторов сразу. Но вспомним, что в резонансной цепи кривая отклика х на единичную силу F зависит от частоты примерно так, как это изображено на фиг. 25.3. В цепи с очень большим значением Q отклик имеет очень острый максимум. Предположим, что обе станции имеют примерно одинаковую мощность, поэтому обе силы имеют примерно одинаковую амплитуду. Отклик равен сумме откликов ха и хb, но на фиг. 25.3 ха громаден, а хb очень мал. Таким образом, хотя оба сигнала одинаковы по силе, в приемнике они проходят через остро резонансную цепь, настроенную на частоту ωа (частоту передач одной из станций), и отклик на эту частоту (станцию) значительно больше отклика на все остальные. Поэтому, несмотря на то что на антенну действуют оба сигнала, полный отклик почти целиком составлен из частоты ωа, и мы можем выбрать ту станцию, какую пожелаем.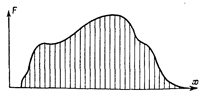 Очень интересен другой способ решения сложных задач. Предположим, что кто-то после больших умственных усилий решил заданную нам задачу в случае одной частной силы — импульсной. Сила внезапно и быстро действует на систему, затем выключается и все опять спокойно. Нам теперь достаточно решить такую задачу лишь в случае единичной силы, потом умножением на подходящее число мы сможем получить любые силы. Мы знаем, что осциллятор откликается на импульсную силу затухающими колебаниями. А как быть в случае другой силы, например силы, изображенной на фиг. 25.4?
Очень интересен другой способ решения сложных задач. Предположим, что кто-то после больших умственных усилий решил заданную нам задачу в случае одной частной силы — импульсной. Сила внезапно и быстро действует на систему, затем выключается и все опять спокойно. Нам теперь достаточно решить такую задачу лишь в случае единичной силы, потом умножением на подходящее число мы сможем получить любые силы. Мы знаем, что осциллятор откликается на импульсную силу затухающими колебаниями. А как быть в случае другой силы, например силы, изображенной на фиг. 25.4?