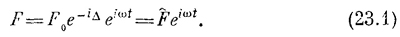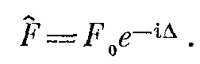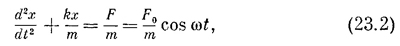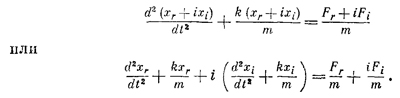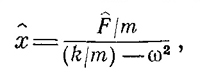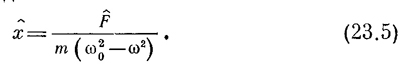| Обучение и материалы |
|---|
| Физический справочник |
| Формулы по физике |
| Шпаргалки по физике |
| Энциклопедия |
| Репетиторы по физике |
| Работа для физиков |
| Быстрый устный счет |
| Виртуальные лабораторные |
| Опыты по физике |
| ЕГЭ онлайн |
| Онлайн тестирование |
| Ученые физики |
| Необъяснимые явления |
| Ваша реклама на сайте |
| Разное |
| Контакты |
| Спецкурс |
|---|
| Фейнмановские лекции |
|
В мире больших скоростей |
Введение в теорию относительности |
|
Лекции по биофизике |
| Лекции по ядерной физике |
| Ускорение времени... |
| Лазеры |
| Нанотехнологии |
| Книги |
| полезное |
|---|
| Смешные анекдоты о физике
Готовые шпоры по физике Физика в жизни Ученые и деньги Нобелевские лауреаты Фото Видео Карта сайта |
| На заметку |
|---|
| Если вам понравился сайт, предлагаем разместить нашу кнопку |
| Дополнительно |
|---|
|
Компьютерные программы по физике 
Физика и юмор 
Онлайн тестирование по физике 
|
Комплексные числа и гармоническое движение
Чтобы применить комплексные числа к ре-шергаю физических задач, проделаем такой трюк. Когда мы изучали осциллятор, то имели дело с внешней силой, пропорциональной cosat. Такую силу F=F0 cos ωt можно рассматривать как действительную часть комплексного числа F = F0 exp(iωt), потому что ехр(iωt) =cos ωt + i sin ωt. Такой переход удобен: ведь иметь дело с экспонентой легче, чем с косинусом. Итак, трюк состоит в том, что все относящиеся к осциллятору функции рассматриваются как действительные части каких-то комплексных функций. Найденное нами комплексное число F, разумеется, не настоящая сила, ибо физика не знает комплексных сил: все силы имеют только действительную часть, а мнимой части взяться просто неоткуда. Тем не менее мы будем говорить «сила» F0exp(iωt), хотя надо помнить, что речь идет лишь о действительной ее части. Рассмотрим еще один пример. Как представить косинусои-дальную волну, фаза которой сдвинулась на Δ? Конечно, как действительную часть F0ехр [i(ωt—Δ)]; экспоненту в этом случае можно записать в виде ехр [i(ωt—Δ)]=ехр(iωt) ехр (-iΔ). Алгебра экспонент гораздо легче алгебры синусов и косинусов; вот почему удобно использовать комплексные числа. Часто мы будем писать так:
Шляпка над буквой будет указывать, что мы имеем дело с комплексным числом, т. е.
Однако пора начать решать уравнения, используя комплексные числа, тогда мы увидим, как надо применять комплексные числа в реальных обстоятельствах. Для начала попытаемся решить уравнение
где F — действующая на осциллятор сила, а х — его смещение. Хотя это и абсурдно, предположим, что х и F — комплексные числа. Тогда х состоит из действительной части и умноженной на i мнимой части; то же самое касается и F. Уравнение (23.2) в этом случае означает
Комплексные числа равны, когда равны их действительные и мнимые части; следовательно, действительная часть х удовлетворяет уравнению, в правой части которого стоит действительная часть силы. Оговорим с самого начала, что такое разделение действительных и мнимых частей возможно не всегда, а только в случае линейных уравнений, т. е. уравнений, содержащих х лишь в нулевой и первой степенях. Например, если бы уравнение содержало член λх2, то, сделав подстановку xr+ixi, мы получили бы λ(xr+ixi)2, и выделение действительной и мнимой частей привело бы нас к λ(x2r - x2i) и 2iλxrxi. Итак, мы видим, что действительная часть уравнения содержит в этом случае член —λх2i. Мы получили совсем не то уравнение, какое собирались решать. Попытаемся применить наш метод к уже решенной задаче о вынужденных колебаниях осциллятора, т. е. об осцилляторе, на который действует внешняя сила. Как и раньше, мы хотим решить уравнение (23.2), но давайте начнем с уравнения
где Feiωt — комплексное число. Конечно, х — тоже комплексное число, но запомним правило: чтобы найти интересующие нас величины, надо взять действительную часть х. Найдем решение (23.3), описывающее вынужденные колебания. О других решениях поговорим потом. Это решение имеет ту же частоту, что и внешняя (приложенная) сила. Колебание, кроме того, характеризуется амплитудой и фазой, поэтому если представить смещение числом х, то модуль его скажет нам о размахе колебаний, а фаза комплексного числа — о временной задержке колебания.Воспользуемся теперь замечательным свойством экспоненты: (d/dt)[x exp(iωt)] = iωx exp(iωt). Дифференцируя экспоненциальную функцию, мы опускаем вниз экспоненту, делая ее простым множителем. Дифференцируя еще раз, мы снова приписываем такой же множитель, поэтому очень просто написать уравнение для х: каждое дифференцирование по времени надо заменить умножением на iω. (Дифференцирование становится теперь столь же простым, как и умножение! Идея использовать экспоненциальные функции в линейных дифференциальных уравнениях почти столь же грандиозна, как изобретение логарифмов, которые заменили умножение сложением. Здесь дифференцирование заменяется умножением.) Таким образом, мы получаем уравнение
[Мы опустили общий множитель eiωt.] Смотрите, как все просто! Дифференциальное уравнение немедленно сводится к чисто алгебраическому; сразу же можно написать его решение
поскольку (iω)2 =—ω2. Решение можно несколько упростить, подставив k/m = ω20, тогда
Это, конечно, то же самое решение, которое уже было нами получено ранее. Поскольку m(ω20 — ω2) — действительное число, то фазовые углы F и х совпадают (или отличаются на 180°, если ω2>ω20). Об этом тоже уже говорилось. Модуль х, который определяет размах колебаний, связан с модулем F множителем 1/m(ω20 — ω2); этот множитель становится очень большим, если ω приближается к ω0. Таким образом, можно достичь очень сильного отклика, если приложить к осциллографу нужную частоту со (если с нужной частотой толкать подвешенный на веревочке маятник, то он поднимается очень высоко). СМОТРИТЕ ТАКЖЕ:Социальные комментарии Cackle |
При использовании материалов сайта ссылка на www.all-fizika.com обязательна.

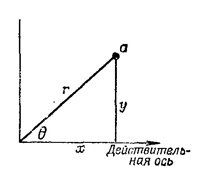 Мы снова будем говорить в этой главе о гармоническом осцилляторе, особенно об осцилляторе, на который действует внешняя сила. Для анализа этих задач нужно развить новую технику. В предыдущей главе мы ввели понятие комплексного числа, которое состоит из действительной и мнимой частей и которое можно изобразить на графике. Действительная часть числа будет изображаться абсциссой, а мнимая — ординатой. Комплексное число а можно записать в виде а=аr+iai, при такой записи индекс г отмечает действительную часть а, а индекс i — мнимую. Взглянув на фиг. 23.1, легко сообразить, что комплексное число a=x+iy можно записать и так: x+iy = r exp(iθ), где r2 = x2 + y2 = (x + iy)(x—iy) = aa * (а* — это комплексно сопряженное к а число; оно получается из а изменением знака i). Итак, комплексное число можно представить двумя способами: явно выделить его действительную и мнимую части или задать его модулем г и фазовым углем θ. Если заданы rи θ, то х и у равны r osθ и r sinθ, и, наоборот, исходя из числа x+iy, можно найти r=√(х2+y2) и угол θ; tgθ равен у/х (т. е. отношению мнимой и действительной частей).
Мы снова будем говорить в этой главе о гармоническом осцилляторе, особенно об осцилляторе, на который действует внешняя сила. Для анализа этих задач нужно развить новую технику. В предыдущей главе мы ввели понятие комплексного числа, которое состоит из действительной и мнимой частей и которое можно изобразить на графике. Действительная часть числа будет изображаться абсциссой, а мнимая — ординатой. Комплексное число а можно записать в виде а=аr+iai, при такой записи индекс г отмечает действительную часть а, а индекс i — мнимую. Взглянув на фиг. 23.1, легко сообразить, что комплексное число a=x+iy можно записать и так: x+iy = r exp(iθ), где r2 = x2 + y2 = (x + iy)(x—iy) = aa * (а* — это комплексно сопряженное к а число; оно получается из а изменением знака i). Итак, комплексное число можно представить двумя способами: явно выделить его действительную и мнимую части или задать его модулем г и фазовым углем θ. Если заданы rи θ, то х и у равны r osθ и r sinθ, и, наоборот, исходя из числа x+iy, можно найти r=√(х2+y2) и угол θ; tgθ равен у/х (т. е. отношению мнимой и действительной частей).