| Обучение и материалы |
|---|
| Физический справочник |
| Формулы по физике |
| Шпаргалки по физике |
| Энциклопедия |
| Репетиторы по физике |
| Работа для физиков |
| Быстрый устный счет |
| Виртуальные лабораторные |
| Опыты по физике |
| ЕГЭ онлайн |
| Онлайн тестирование |
| Ученые физики |
| Необъяснимые явления |
| Ваша реклама на сайте |
| Разное |
| Контакты |
| Спецкурс |
|---|
| Фейнмановские лекции |
|
В мире больших скоростей |
Введение в теорию относительности |
|
Лекции по биофизике |
| Лекции по ядерной физике |
| Ускорение времени... |
| Лазеры |
| Нанотехнологии |
| Книги |
| полезное |
|---|
| Смешные анекдоты о физике
Готовые шпоры по физике Физика в жизни Ученые и деньги Нобелевские лауреаты Фото Видео Карта сайта |
| На заметку |
|---|
| Если вам понравился сайт, предлагаем разместить нашу кнопку |
| Дополнительно |
|---|
|
Компьютерные программы по физике 
Физика и юмор 
Онлайн тестирование по физике 
|
Мнимые экспоненты
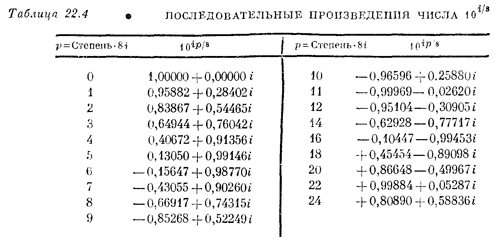
Чтобы лучше понять, что такое число в мнимой степени, вычислим последовательные степени десяти. Мы не будем каждый раз удваивать степень, чтобы не повторять табл. 22.3, и посмотрим, что случится с действительной частью после того, как она станет отрицательной. Результат можно увидеть в табл. 22.4.
В этой таблице собраны последовательные произведения числа 10i/8. Видно, что ж уменьшается, проходит через нуль, достигает почти —1 (в промежутке между р=10 и р = 11 величина точно равна —1) и возвращается назад. Точно так же величина у ходит взад-вперед.
Каковы свойства алгебраического косинуса cos t и алгебраического синуса sin t? Прежде всего x2 + y2= 1; это мы уже доказали, и это верно для любого основания, будь то 10 или е. Следовательно, cos2t + sin2t = 1. Мы знаем, что eit = 1+it для малых t; значит, если t— близкое к нулю число, то cos t близок к единице, a sin t близок к t. Продолжая дальше, мы придем к выводу, что все свойства этих замечательных функций, получающихся в результате возведения в мнимую степень, в точности совпадают со свойствами тригонометрического синуса и тригонометрического косинуса. А как обстоит дело с периодом? Давайте найдем его. В какую степень надо возвести е, чтобы получить i? Иными словами, чему равен логарифм i по основанию е? Мы вычислили уже логарифм i по основанию 10; он равен 0,68226i; чтобы перейти к основанию е, мы умножим это число на 2,3025 и получим 1,5709i. Это число можно назвать «алгебраическим π/2». Но поглядите-ка, оно отличается от настоящего π/2 всего лишь последним десятичным знаком, и это просто-напросто следствие наших приближений при вычислениях! Таким образом, чисто алгебраически возникли две новые функции — синус и косинус; они принадлежат алгебре и только алгебре. Мы пошли по их следам и обнаружили, что это те же самые функции, которые так естественно возникают в геометрии. Мы отыскали мост между алгеброй и геометрией. Подводя итог нашим поискам, мы напишем одну из самых замечательных формул математики
Вот она, наша жемчужина.
СМОТРИТЕ ТАКЖЕ:Социальные комментарии Cackle |
При использовании материалов сайта ссылка на www.all-fizika.com обязательна.

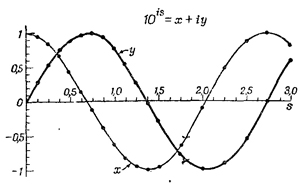 Точки на фиг. 22.1 соответствуют числам, приведенным в табл. 22.4, а соединяющие их линии помогают следить за изменением х я у. Видно, что числа хну осциллируют; 10i/8 повторяет себя. Легко объяснить, почему так происходит. Ведь i в четвертой степени — это i2 в квадрате. Это число равно единице; следовательно, если 100,68i равно i, то, возведя это число в четвертую степень, т. е. вычислив 102,72i, мы получим +1. Если нужно получить, например, 103,00i, то нужно умножить 102,72i на 100,28i. Иначе говоря, функция 10is повторяется, имеет период. Мы уже знаем, как выглядят такие кривые! Они похожи на график синуса или косинуса, и мы назовем их на время алгебраическим синусом и алгебраическим косинусом. Теперь перейдем от основания 10 к натуральному основанию. Это только изменит масштаб горизонтальной оси; мы обозначим 2,3025s через t и напишем 10is=eit, где t — действительное число. Известно, что eit =x+iy, и мы запишем это число в виде
Точки на фиг. 22.1 соответствуют числам, приведенным в табл. 22.4, а соединяющие их линии помогают следить за изменением х я у. Видно, что числа хну осциллируют; 10i/8 повторяет себя. Легко объяснить, почему так происходит. Ведь i в четвертой степени — это i2 в квадрате. Это число равно единице; следовательно, если 100,68i равно i, то, возведя это число в четвертую степень, т. е. вычислив 102,72i, мы получим +1. Если нужно получить, например, 103,00i, то нужно умножить 102,72i на 100,28i. Иначе говоря, функция 10is повторяется, имеет период. Мы уже знаем, как выглядят такие кривые! Они похожи на график синуса или косинуса, и мы назовем их на время алгебраическим синусом и алгебраическим косинусом. Теперь перейдем от основания 10 к натуральному основанию. Это только изменит масштаб горизонтальной оси; мы обозначим 2,3025s через t и напишем 10is=eit, где t — действительное число. Известно, что eit =x+iy, и мы запишем это число в виде

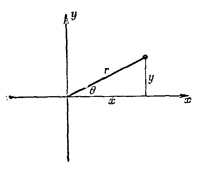 Связь между алгеброй и геометрией можно использовать для изображения комплексных чисел на плоскости; точка на плоскости определяется координатами х и у (фиг. 22.2). Представим каждое комплексное число в виде x+iy. Если расстояние точки от начала координат обозначить через r, а угол радиуса-вектора точки с осью х — через θ, то выражение x+iy можно представить в виде reiθ. Это следует из геометрических соотношений между х, у, r и θ. Таким образом, мы объединили алгебру и геометрию. Начиная эту главу, мы знали только целью числа и умели их считать. Зато у нас была небольшая идея о могуществе шага в сторону и обобщения. Используя алгебраические «законы», или свойства чисел, сведенные в уравнения (22.1), и определения обратных операций (22.2), мы смогли создать не только новые числа, но и такие полезные вещи, как таблицы логарифмов, степеней и тригонометрические функции (они возникли при возведении действительных чисел в мнимые степени), и все это удалось сделать, извлекая много раз квадратный корень из десяти!
Связь между алгеброй и геометрией можно использовать для изображения комплексных чисел на плоскости; точка на плоскости определяется координатами х и у (фиг. 22.2). Представим каждое комплексное число в виде x+iy. Если расстояние точки от начала координат обозначить через r, а угол радиуса-вектора точки с осью х — через θ, то выражение x+iy можно представить в виде reiθ. Это следует из геометрических соотношений между х, у, r и θ. Таким образом, мы объединили алгебру и геометрию. Начиная эту главу, мы знали только целью числа и умели их считать. Зато у нас была небольшая идея о могуществе шага в сторону и обобщения. Используя алгебраические «законы», или свойства чисел, сведенные в уравнения (22.1), и определения обратных операций (22.2), мы смогли создать не только новые числа, но и такие полезные вещи, как таблицы логарифмов, степеней и тригонометрические функции (они возникли при возведении действительных чисел в мнимые степени), и все это удалось сделать, извлекая много раз квадратный корень из десяти!